
Collegedunia Team Content Curator
Content Curator
Right angle is where the angle is exactly 90 degrees. In a right angle, the two arms are always perpendicular to each other. Angles can be divided into six types. The six different types of angles are acute angle, obtuse angle, right angle, straight angle, full rotation, reflex angle. The right angle is present in several geometrical figures.
| Table of Content |
Key Takeaways: Angle, Types of Angles, Right Angle, Construction, 90 degrees, Perpendicular
What is an Angle?
An angle is formed when two rays are attached at one point, and direct at different or the same direction. The angle represents how far the two rays are from each other. An angle is represented as ∠, but they are measured in degrees, represented as °. The angle is measured using a protractor.
Sections of an Angle:
An angle is composed of two main parts:
- Arms: These are the rays that make up the angle. They join together at a point to make up the angle.
- Vertex: It is the point at which the rays join together.
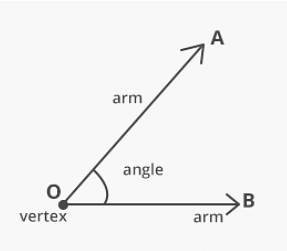
Parts of an Angle
Read More:
| Angle Formula | Introduction to Three-Dimensional Geometry |
| Class 10 Mathematics Chapter 6 Triangles | Similarity of Triangles |
Types of Angles
The different types of angles are listed below with their definitions:
| Angles | Definition |
|---|---|
| Acute angle | An acute angle is more than 0° and less than 90°, thus it lies between 0° and 90°. |
| Obtuse angle | An obtuse angle is more than 90° and less than 180°, thus it lies between 90° and 180° |
| Right angle | Right angles have an exact value of 90° |
| Straight angle | Straight angles have an exact value of 180°. It is like a straight line. |
| Reflex angle | As we know an angle is made by two rays. An acute angle is smaller than 90°. This is on the inner side of the rays. However, the outer side has a bigger angle. This bigger angle is the reflex angle. |
| Complete angle | This is an angle having a value of 360°. It is formed when two rays coincide. |
| Interior angle | These are the angles present inside a geometrical figure. |
| Exterior angle | Exterior angles are the angles present outside a geometrical figure. They are formed by extending one of the sides of the geometrical figure. |

Exterior and Interior Angle
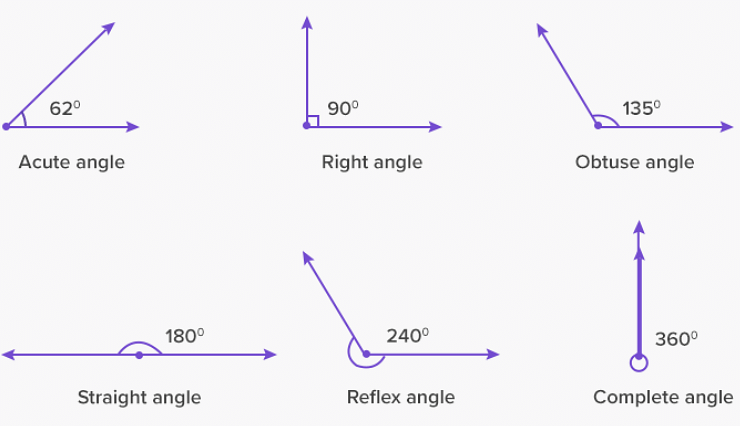
Types of Angle
Read Also:
What is Right Angle?
Right angles have an exact value of 90°. This angle is formed when two rays are perpendicular on each other.
How to Construct a Right Angle?
There are two methods to construct a 90-degree angle in mathematics. These two methods are, using a protractor, and using geometric construction.
Using a Protractor:
- Firstly, draw a straight line using a scale.
- Mark a point on the line.
- Coincide the line, and point of the protractor with the line and point drawn.
- Mark a point on the paper, where the protractor marks 90 degrees.
- Draw a line joining both the points.
- This would give a 90-degree angle.
Read Also:
Using Geometric Construction:
- Firstly, draw a straight line using a scale, line segment CD.
- Mark a point on the line, let's mark it A.
- Take that point as the center, and draw an arc bisecting the line at any point, let's mark that bisecting point B.
- Now take B as the center of the circle, and draw an arc bisecting the previous arc drawn. Let's name its point E.
- Now using E as the center draw two arcs, one a the top, another bisecting the previous arc. Let’s name this point G.
- Now using G as the center draw another arc, which bisects the first arc drawn using E as the center. This intersection can be termed F.
- Now join F and A, this will produce a right angle.

Construction of Right Angle
Read More:
Things To Remember
- An angle is formed when two rays are attached at one point, and directed at different or the same direction.
- The angle represents how far the two rays are from each other. An angle is represented as ∠, but they are measured in degrees, represented as °.
- The six different types of angles are acute angle, obtuse angle, right angle, straight angle, full rotation, reflex angle.
- An angle is composed of two main parts Arms, are the rays which make up the angle. They join together at a point to make up the angle. Vertex is the point at which the rays join together.
- An acute angle is smaller than 90°. This is on the inner side of the rays. However, the outer side has a bigger angle. This bigger angle is the reflex angle.
Read Also:
Sample Questions
Ques 1: What is an angle? (2 marks)
Ans: An angle is formed when two rays are attached at one point, and direct at different or the same direction. The angle represents how far the two rays are from each other. An angle is represented as ∠, but they are measured in degrees, represented as °. An angle is composed of two main parts Arms, are the rays which make up the angle. They join together at a point to make up the angle. Vertex, is the point at which the rays join together.
Ques 2: What are the different types of angles? (2 marks)
Ans: All these angles can be divided into six types. The six different types of angles are, acute angle, obtuse angle, right angle, straight angle, full rotation, reflex angle. Acute angle is more than 0° and less than 90°. Obtuse angle is more than 90° and less than 180°. Right angles have an exact value of 90°. Straight angles have an exact value of 180°. Full rotation angle is 360 degrees.
Ques 3: What is a right angle? (2 marks)
Ans: Right angles have an exact value of 90°. This angle is formed when two rays are perpendicular on each other. There are two methods to construct any angle in mathematics. These two methods are, using a protractor, and using geometric construction.
Ques 4: What are exterior and interior angles? (2 marks)
Ans: Exterior angles are the angles present outside a geometrical figure. They are formed by extending one of the sides of the geometrical figure. And interior angles are the angles present inside a geometrical figure.
Ques 5: What is reflex, and complete angle? (2 marks)
Ans: As we know an angle is made by two rays. An acute angle is smaller than 90°. This is on the inner side of the rays. However the outer side has a bigger angle. This bigger angle is the reflex angle. Complete angle is an angle having a value 360°. It is formed when two rays coincide.
Ques 6: In the following right angle, find the value of the missing angle. (2 marks)

Ans: There are two angles, one of them is 62 degrees. The other angle would be 90- the first angle. Thus the other angle is 90-62 = 28 degrees.
Ques 7: In the following right angle, find the value of the missing angle. (2 marks)

Ans: There are two angles, one of them is 43 degrees. The other angle would be 90- the first angle. Thus the other angle is 90-43 = 47 degrees.
Ques 8: In the following straight angle, find the value of the missing angle. (2 marks)

Ans:There are two angles, one of them is 108 degrees. The other angle would be 180- the first angle. Thus the other angle is 180-108 = 72 degrees.
Ques 9: In the following straight angle, find the value of the missing angle. (2 marks)
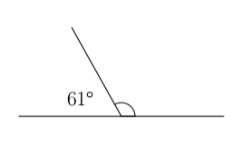
Ans: There are two angles, one of them is 61 degrees. The other angle would be 180- the first angle. Thus the other angle is 180-61 = 119 degrees.
Ques 10: In the following right-angled triangle, find the value of the missing angle. (2 marks)

Ans: Angle 1 = 90 degrees
Angle 2 = 40 degrees
Angle 3 = x degrees
Sum of three angles of triangle = 180 degrees
Thus, 40 + 90 + x = 180 degrees
X = 180 - 130
X = 50 degrees.
Read Also:






Comments