
Collegedunia Team Content Curator
Content Curator
Area of the square using diagonal means measuring area of a square through two nonadjacent vertices of the square. A diagonal line means a line that can be stretched from one corner of a square to the other corner by its center. The diagonals of a square are always equal in size and they bisect each other at right angles. To calculate a polygon’s diagonals, the same formula of the square is used. When the side length of a square is known then the formula for the diagonal of a square is used to measure the length of the diagonal.
Also Read: Surface Areas and Volumes
| Table of Content |
Keyterms: Square, Line, Polygon, Right angle, Side length, Diagonal, congruent isosceles
Read More: Geometry
Diagonal of the Square
[Click Here for Sample Questions]
The lines that join the two opposite vertices of a square are called diagonal. A square has two diagonals.

Diagonal Of a Square
The properties of diagonal are the following:
- The diagonals of a square are the perpendicular bisectors of each other.
- They are equal in length.
- Diagonals divide the square into two right-angled triangles which are congruent isosceles.
Also Read:
| Related Articles | ||
|---|---|---|
| Circles | Triangles | Similarities of Triangle |
| Pythagoras Theorem | Trigonometric Identities | Construction Formula |
How to Derive the Area of a Square Using Diagonal?
[Click Here for Sample Questions]
The most common way to find out the area of a square is to square the length of its sides. Hence, a correct measure of the length of the sides of the square is necessary.
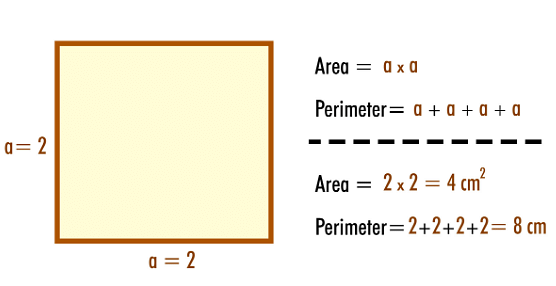
Area of a Square
When the sides of a square are replaced by the diagonals it is very important to find out the relation between the diagonal of a square and its side.
Also Read: Nature of Roots of Quadratic Equation
Relation Between the Diagonal and the Side of a Square
[Click Here for Sample Questions]
A square can be divided into two right-angled triangles in which the triangle’s hypotenuse is equal to the diagonals of the square. Pythagoras theorem can be applied to show the relation between the sides of the right-angled triangle and the hypotenuse. Therefore, it also represents the relation between the diagonal of a square.

Diagonal and side of a square
Consider the angle θ, making an angle with the side AB and the diagonal AC as shown in the image.
Sin θ = a/ d ….(1)
We know that, for a square, all the angles are right angles.
Since a diagonal divides the angle equally,
We can say that θ = 45°
Substituting in Eq(1),
Sin 45° = a/ d
As Sin 45° = 1/√2
1/√2 = a/ d
d = √2 x a
Therefore,
Diagonal = √2 x side
Also Read: Section Formula
Measuring the Area of a Square Using Diagonal
[Click Here for Sample Questions]
Area of square = side × side
When diagonal is equal to √2 × side
Then side = 1/ √2 diagonal.
The formula of area of the square using diagonal =
1/ √2 diagonal × 1/ √2 diagonal
=1/2 (diagonal)2
Area of square = ½ d2
The area of the square using diagonal is =½ d2
Read More: Triangle
Things to Remember
- A diagonal line means a line that can be stretched from one corner of a square to the other corner by its center.
- The most common way to find out the area of a square is to square the length of its sides.
- Pythagoras theorem can be applied to show the relation between the sides of the right-angled triangle and the hypotenuse.
- The formula of area of the square using diagonal is ½ d2.
- The length of the diagonal can be calculated by using the formula, Diagonal = √2 x side.
Also Read:
Sample Questions
Ques. Write the diagonal formula of the square. (2 marks)
Ans. The diagonal formula of the square is d = a√2. Here, ‘d’ represents diagonal, and ‘a’ represents the side of the square. This formula is derived from the Pythagoras Theorem.
Ques. How to find out the length of the diagonal of a square? (2 marks)
Ans. The length of the diagonal of a square can be found by multiplying the length of one side by the square root of 2. When the length of one side is x, then the diagonals of the square cross (intersect) at a 90° angle.
Ques. The angles of a quadrilateral are in the ratio of 2 : 3 : 5 : 8. Find the measure of each angle. (2 marks)
Ans. Sum of all interior angles of a quadrilateral = 360°
Let the angles of the quadrilateral be 2x°, 3x°, 5x° and 8x°.
2x + 3x + 5x + 8x = 360°
⇒ 18x = 360°
⇒ x = 20°
Hence the angles are
2 × 20 = 40°,
3 × 20 = 60°,
5 × 20 = 100°
and 8 × 20 = 160°
Ques. What is the area of a square? (2 marks)
Ans. A square’s all the sides are of equal measure. As all the sides are equal, the area of a square would be length times width that is equal to side × side. Therefore, the area of a square side square.
Ques. Can we say the diagonal of a square is equal to its sides? (2 marks)
Ans. No, the diagonal of a square is not equal to its sides. The formula to calculate the diagonal of a square is (d) = √2 × s, here, ‘s’ represents the side of the square.
Ques. What will be the area of a square of 4 cm? (2 marks)
Ans. Consider the side-length of the square is 4 cm. Hence, using the counting squares method the area of the square will be 16 cm2.
Ques. What are the relations between diagonal and side of a square? (2 marks)
Ans. The relations between diagonal and side of a square is given by the formula,
Diagonal =√2 x a
Ques. How do you find the total number of diagonals in a square? (2 marks)
Ans. To find out the total number of diagonals in a square you need to multiply the number of diagonals per vertex (n-3) by the total number of vertices, n, and then divide it by 2.
Ques. In a square, how many diagonals are there? (2 marks)
Ans. In a square, there are two diagonals of equal length. These diagonals intersect at the center of the square. A pentagon of regular size has five diagonals and all these diagonals have the same length.
Ques. In the parallelogram given alongside if m∠Q = 110°, find all the other angles. (2 marks)
Ans. Given m∠Q = 110°
Then m∠S = 110° (Opposite angles are equal)
Since ∠P and ∠Q are supplementary.
Then m∠P + m∠Q = 180°
⇒ m∠P + 110° = 180°
⇒ m∠P = 180° – 110° = 70°
⇒ m∠P = m∠R = 70° (Opposite angles)
Hence m∠P = 70, m∠R = 70°
and m∠S = 110°
Ques. ABCD is a rhombus. Find the values of x, y and z. (2 marks)
Ans. AB = BC (Sides of a rhombus)
x = 13 cm.
Since the diagonals of a rhombus bisect each other
z = 5 and y = 12
Hence, x = 13 cm, y = 12 cm and z = 5 cm.
Ques. Length and breadth of a rectangular wire are 9 cm and 7 cm respectively. If the wire is bent into a square, find the length of its side. (2 marks)
Ans. Perimeter of the rectangle = 2 [length + breadth]
= 2[9 + 7] = 2 × 16 = 32 cm.
Now perimeter of the square = Perimeter of rectangle = 32 cm.
Side of the square =
32/4 = 8 cm.
Hence, the length of the side of the square = 8 cm.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:






Comments