
Jasmine Grover Content Strategy Manager
Content Strategy Manager
When two perpendicular straight lines bisect each other, it forms two sets of vertical angles. It forms a pair of acute and another pair of obtuse angles. The slope of the bisecting lines determines the absolute value of the angles.
The angle between two parallel lines is zero and that between a non-parallel, perpendicular line is 90 degrees. In this article, we will find the angle between two non-perpendicular lines, which depends on the slopes formed by the bisecting lines. One should keep in mind that it is not possible to calculate the angle formed by intersection if a line is parallel to the y- axis.
| Table of Content |
Keyterms: Angle, Line, Straight line, Slope, Bisecting line, Acute angle, Parallel line, Intersection, Non-perpendicular lines
Derivation - The angle between two straight lines
[Click Here for Sample Questions]
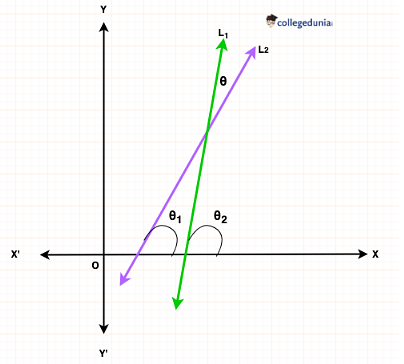
The angle between two straight lines
Let two lines, L1 and L2 intersect at a point, forming one acute and another obtuse angle,
Let = acute angle
θ+θ1 + x = 180 … (i)
x +θ2 = 180 … (ii) (as angle x and 2 forms a linear pair)
θ+θ1 + x = x +θ2 = 180 (by equating (i) and (ii)
θ+θ1 + x – x = x +θ2 – x (by subtracting x from both sides)
We get, θ+1 = 2
θ + 1 = 2
θ + θ1- θ1 = 2 – 1 (by subtracting 1 from both side)
We get, = θ2- θ1
tan = tan (θ2– θ1) (applying tangent on both sides)
tan θ = \(\frac{tan \theta 2 - tan \theta 1}{1 + tan \theta 1 tan \theta 2}\)(using the formula of tangent)
From the slope of the line, we know that tan= m
Thus substituting,
tanθ1 = m1 and tanθ2 = m2
θ= a2-a1
Substituting the value of 1 and 2
tanθ = (m2 - m1)/(1 + m1m2)
The value of tan will be positive if is acute and negative if is obtuse
The angle between two lines in coordinate geometry
Another way to find the angle between two lines is by finding out the slope of each line and then by using the formula to evaluate the angle between two lines.
The formula for determining the slope of a line is-
tanθ= ± (m1-m2)/ (1+m1m2)
The angle between two lines : Important formulas
- If the lines are non-parallel lines, m1 and m2 = two slopes of these lines, and = angle between the lines,
tanθ= (m2 - m1)/(θ1+m1m2)
- If the lines are perpendicular, i.e, = 90°, then,
1/tanθ= 0
1+ (m1m2)/(m1-m2) = 0
1+m1m2 = 0
m1m2 = -1
- If the lines are parallel, i.e,= 0°, then
tanθ= 0
(m1-m2)/(1+m1m2)= 0
m1-m2 = 0
m1= m2
- A line with endpoints (x1, y1) and (x2, y2), the slope of the line is
m = (y2-y1)/(x2-x1)
Sample Questions
Question: Find out the distance of the line given by 4x-y=0 from a given point P(4,1), making a 135° angle with the positive x-axis. (2 marks)
Ans. Given line is 4x-y= 0 ... (i)
Slope of the second line is tan 135° = -1
Equation of the line with slope -1 through the point P(4,1) is
y-1 = -1(x-4) or x+y-5=0 ... (ii)
Solving (i) and (ii), we get x=1 and y=4 so that the point of intersection of the two lines is Q(1, 4).
Now distance of line (i) from the point P(4, 1) along the line (ii) = the distance between the points P(4, 1) and Q(1, 4) = √(1-4)2+(4-1)2 = 3√2 units.
Question: Find the acute angle between the lines y= 3x + 1 and y= -4x + 3 (2 marks)
Ans. m1 = 3 and m2= -4
tanθ = ± (m1- m2)/(1+m1*m2)
tanθ = ± (3-(-4))/(1+ 3* -4)
tanθ = ± (7)/(1+(-12))
tanθ = ± (7)/(-11)
tanθ = ± (7/11)
tanθ = 0.636
= tanθ-1 (0.636)
Question: Find the value of k, if the following lines are concurrent,
2x+y-3=0,
5x+ky-3= 0, and
3x-y-2= 0 (3 marks)
Ans. Three lines are said to be concurrent if they pass through a common point which is the point of intersection of any two lines lying on the third line. Here given lines are
2x + y- 3 = 0 … (1)
5x + ky - 3 =0 … (2)
3x - y - 2 =0 … (3)
Cross multiplying (1) and (2)
\(\frac{x}{(-2-3)} = \frac{y}{(-9+4)} = \frac{1}{(-2-3)}\) or x=1 , y=1Hence, for these two lines, the point of intersection is (1,1). Since, the above three lines are concurrent in nature, the point (1,1) will also satisfy equation (2), so that
5(1) + k(1) - 3 = 0 or k = -2
Question: Find the equation of a line which is perpendicular to the line, represented by x-2y+3= 0, and passing through a point (1,-2). (2 marks)
Ans. Given line x-2y+3=0 which can be written as
y= (1/2)x + 3/2 …(1)
Slope of the line (1), represented by m1 is 1/2.
Therefore, slope of the line that is perpendicular to line (1) is given by
m2 = -(1/m2) = -2
The equation of the line passing through a given point (1,-2) and having -2 as slope is
y(-2) = -2(x-1) or y= – 2x
Question: Find the image of the point p(1, 2) in the line x-3y+4=0, assuming that, for a point, straight lines work as the plane mirror. (3 marks)
Ans. Let q (h,k) be the image of the given point p(1,2) in the line
x-3y+4=0 ... (1)
Therefore, the line (1) is the perpendicular bisector of the line segment pq
Hence, slope of the line pq= -1/slope of the line x - 3y + 4 = 0
So that (k-2)/(h-1) = -1/(1/3) or 3h+k = 5 …….. (2)
And the midpoint of pq which is (h+1)/2, (k+2)/2 will satisfy the equation (1) so that
[(h+1)/2] - 3[(k+2)/2] + 4 = 0 or h - 3k = -3 …… (3)
Solving (2) and (3), we get h = 6/5 and k= 7/5
Hence the image of the point (1, 2) in the line x-3y+4=0 is 6/5, 7/5
Question: Find the equation of a line that is perpendicular to another line x-2y+3=0 and passes through the point (1,-2). (2 marks)
Ans. Given line x-2y+3=0 can be written as
y = 12x + 32 … (1)
The slope of this line (m1)= 1/2.
Therefore, the slope of the line perpendicular to line(1) is
m2 = - (1/m2) = -2
Equation of the line having slope -2, that passes through the point (1,-2) is
y-(-2) = -2(x-1)
or y = -2x
Question: A line which passes through the points (4, 8) and (-2, 6) is perpendicular to the line through the points (8,12) and (x, 24). Find the value of x. (2 marks)
Ans. The Slope of the line passing through the given points (-2,6) and (4,8) is-
m1 = (8-6)/4-(-2) = 2/6 = 1/3
The slope of the line through the points (8,12) and (x, 24) is given as-
m2 = (24-12)/(x-8) = 12/ ( x-8)
Since two lines are perpendicular
m1m2 = -1, which gives
1/3*[12/(x-8)] = -1 or
x = 4





Comments