
Content Curator
Exterior angle theorem states that, if the side of a triangle is produced further, the exterior angle formed is equal to the sum of the opposite two interior angles. Exterior angle theorem defines the relationship between the exterior angles and interior angles and can be proved easily with the help of angle sum property of the triangle.
| Table of Content |
Key takeaways: Exterior angle property of triangle, Angle sum property of triangle, Linear angle sum property.
Exterior Angle Theorem
[Click Here for Sample Questions]
Exterior angle property of triangle states that if the side of the angle is produced, the exterior angle of the triangle formed is equal to the sum of the opposite 2 interior angles.
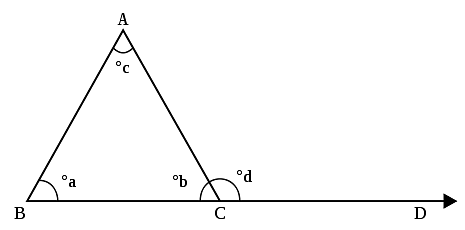
Exterior Angle Theorem
Let’s look at the proof of this theorem.
Read More: Surface areas
Proof
[Click Here for Sample Questions]
The following theorem can be proved in two alternative ways.
To Prove
- Angle sum property of triangle: The sum of all the interior angles of a triangle is equal to 180°.
- The alternate interior angles are equal in case of parallel lines.
- The corresponding angles of a transverse are equal in case of parallel lines.
Given: A triangle ABC with side CB extended till D. The exterior angle formed is ∠ABD. ∠BAC and ∠ACB are two opposite interior angles.
To prove: ∠ABD=∠BAC+∠BCA

Figure-1
Proof - 1
ABC is a triangle. (see figure-1)
According to the angle sum property of triangle,
∠ABC + ∠BCA + ∠BAC = 180°
I.e- ∠ABC=180°- (∠BCA+ ∠BAC)….. (a)
Also, by linear pair, ∠ABC+∠ABD=180°…..(b)
From (a) and (b),
180°- (∠BCA+ ∠BAC) + ∠ABD=180°
180°- (∠BCA+ ∠BAC) + ∠ABD=180°
I.e- ∠BCA + ∠BAC = ∠ABD
Hence the exterior angle theorem is proved.
Proof - 2
A triangle ABC with line CB extended will D.
BE is parallel to CA and AB is the transverse. (see figure-2)
∠1 = ∠3 {alternate angles, as CA parallel to BE and AB is the transverse}... (A)
∠2 = ∠4 {corresponding angles as CA parallel to BE and CD is the transverse}...(B)
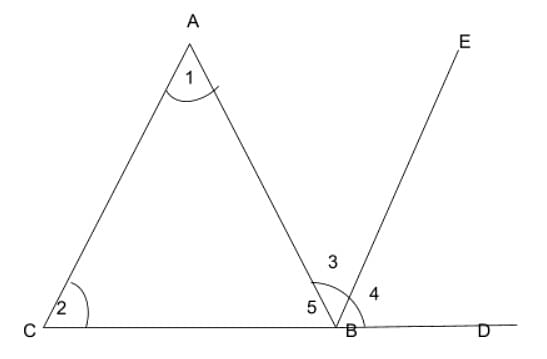
Figure-2
Adding (A) and (B)
∠1 + ∠2 = ∠3 + ∠4
I.e- ∠BAC + ∠BCA = ∠ABD
Hence the exterior angle theorem of the triangle is proved.
Also Read:
Things to Remember
- The sum of all the interior angles of a triangle is equal to 180°.
- The exterior angle formed is equal to the sum of two opposite interior angles.
- The exterior angle formed is always greater than either of the two interior angles.
- The sum of all exterior angles of a triangle is 360°.
- Vertically opposite angles are equal.
Sample Questions
Ques. Find the value of missing angles i.e ∠ABD. (2 Marks)
Ans. ∠BAC=50°
∠ACB=30°
According to exterior angle theorem, ∠ABD= ∠BAC+∠ACB
I.e ∠ABD= 50+30=80°
∠ABD=80 °
Ques. Find the value of 4, if 1=90 ° 3=30 ° (2 Marks)
Ans.
Given-
1=90 °
3=30 °
So, 2= 180°-(1+3) (angle sum property of triangle)
→ 180°-(90+30)
→ 180°-120°
→ 60°
Also,
4 =1+2 (exterior angle theorem)
→ 90°+60°
→ 150°
Ques. Find the values of 2,3, and 4 if the value of 1=60° and 5= 80° and CA is parallel to BE with AB and CD being the transverse. (5 Marks)
Ans.

Angle 1= 60° ; 5= 80°
Therefore,
2= 180°-(1+5) ……(angle sum property of triangle)
→ 180°-140°
→ 40°
Angle ∠2 = 40°
∠1=∠3……(alternate angles equal in parallel lines)
Therefore, ∠3=60°
∠4=∠2….. (corresponding angles equal in parallel lines)
Therefore, ∠4= 40°
Ques. Find the missing angles from the figure. (5 Marks)
Ans. In triangle SQR,
∠SRQ=20° {GIVEN}
∠RSQ=90° {GIVEN}
Therefore, by angle sum property of triangle,
∠RQS=180°-(20+90)
→ 180°-110°
→ 70°
Therefore, ∠RQS=70°
In triangle PQT,
∠RQS= ∠PQT=70° {PROVED ABOVE}
∠TPQ= 30° {GIVEN}
Therefore, by exterior angle property of triangle,
∠TPQ+∠PQT=∠PTR
∠PTR=30°+70°
=100°
Therefore, ∠PTR=100°
Ques. Find ∠POR. (5 Marks)
Ans. In triangle SQR,
∠SRQ=20° {GIVEN}
∠RSQ=90° {GIVEN}
Therefore, by angle sum property of triangle,
∠RQS=180°-(20+90)
→ 180°-110°
→ 70°
Therefore, ∠RQS=70°
In triangle PQT,
∠RQS= ∠PQT=70° {PROVED ABOVE}
∠TPQ= 30° {GIVEN}
Therefore, by exterior angle property of triangle,
∠TPQ+∠PQT=∠PTR
∠PTR=∠OTR = 30°+70°
→ 100°
Therefore, ∠PTR=∠OTR=100°
In triangle OTR,
∠OTR+∠ORT+∠ROT= 180°
Therefore,
∠ROT=180°-(20°+100°)
→ 60°
Now, ∠POR+ ∠ROT =180° {LINEAR ANGLE SUM PROPERTY}
Therefore,
∠POR=180°-60°
→ 120°
Hence,
∠POR=120°
Ques. Find the missing angle if the triangle is an equilateral triangle and CD bisects ∠ACB. (2 marks)
Ans. Since ABC is an equilateral triangle,
Therefore, all the angles are equal and are equal to 60°.{equilateral triangle property}
Therefore,
∠BCD=30° {given, since, CD bisects ∠ACB}
By exterior angle sum property of a triangle,
∠ADC= ∠BCD+ ∠DBC
→ 30°+60°
→ 90°
Therefore, ∠ADC = 90°
Ques. Find angle 5, if l is parallel to m and n is the transverse. Also, ∠2=50°and ∠1=50°. (2 marks)
Ans. ∠1=∠3 {vertical angle property: vertically opposite angles are equal}
In triangle, ABC, ∠3+∠2=∠5 {exterior angle property of triangle}
Therefore, ∠5= 50°+50°
→ 100°
Hence, ∠5=100°
Ques. Find ∠XZP, if ∠ZXY=80° and ∠ZYX=70° (5 marks)
Ans. By exterior angle property of triangle,
∠YZQ= ∠ZXY+∠ZYX
→ 70°+80°
→ 150°
Now, as vertically opposite angles are equal,
Therefore, ∠YZQ=∠XZP
→ 150°
Hence,
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check More:





Comments