
Content Writer
Area and Perimeter is a branch of geometry that deals with the calculation of the length, height and volume of a particular geometric shape. These formulas can be used for any object, whether it is regular object or irregular object.
- Both area and perimeter are two-dimensional in nature.
- Each geometrical shape has a unique area and perimeter.
- Area is the measurement of a surface that is covered by a closed figure.
- The SI unit of area is square meter.
- Perimeter is the length of the boundary of a closed figure.
- The SI unit of perimeter is meter.
- Formulas can be used to find the area and perimeter of various geometrical figure.
- These formulas are used in everyday life such as measuring the area of a swimming pool.
Read More: Difference between Area and Volume
Key Terms: Area, Perimeter, Volume, Radius, Rectangle, Triangle, Circle, Square, Rhombus, Parallelogram, Trapezoid
Area
[Click Here for Sample Questions]
Area is defined as a two-dimensional space occupied by any object. The formula depends upon the dimensions and properties of a figure. Let's assume that you are asked to paint a door of your house.
- Now, you need to know the area of the door first to determine the amount of paint required to paint that door.
- Different shapes occupy different areas.
- The area occupied by a triangle is different to the area occupied by a circle.
- If two objects have the same shape, then their area will be equal if their dimensions are equal.
- The area of these objects is calculated in square units (sq units).
Area
Read More:
| Related Articles | ||
|---|---|---|
| Quadratic Equations | Rationalize the Denominator | Similarities of Triangle |
| Pythagoras Theorem | Trigonometric Identities | Construction Formula |
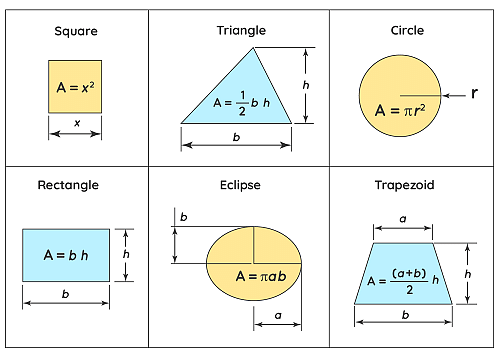
Area of Various Shapes
[Click Here for Sample Questions]
The formulas of area for different objects with different shapes are as follows:
| Shapes | Area Formulas | Variables |
|---|---|---|
| Triangle | ½×b×h | b = base h = height |
| Rectangle | l×w | l = length w = width |
| Square | a² | a = sides of the square |
| Semicircle | ½πr² | π = 22/7 or 3.1416 r = radius of the circle |
| Circle | πr² | π = 22/7 or 3.1416 r = radius of the circle |
| Trapezoid | ½(a+b) h | a = base 1 b = base 2 h = vertical height |
| Rhombus | a×h | a = side of the rhombus h = height |
| Parallelogram | b×h | b = base h = height |
Read More: Section Formula
Perimeter
[Click Here for Sample Questions]
Perimeter is the length of the boundary covered by any object. The length of a book is its perimeter. Now, depending upon the shape and length of the objects, perimeter changes.
- We have to know certain measurements of an object to calculate its perimeter.
- Depending upon its shape, the measurements change.
- For any curved shape, perimeter is known as circumference.
- Perimeter value of a circular wheel calculate the distance covered in one revolution.
- Some real-life example of perimeter includes length of a lawn and size of a photo-frame.
Perimeter
Read More: Frequency Polygons
Perimeter of Various Shapes
[Click Here for Sample Questions]
The formulas of perimeter for different objects with different shapes are tabulated below.
| Shapes | Perimeter Formula | Variables |
|---|---|---|
| Triangle | Sum of the length of all sides (a+b+c) | a, b, c are the length of the sides. |
| Rectangle | 2 (l+w) | l = length w = width |
| Square | 4a | a = length of a side |
| Semicircle | πr+2r | r = radius of the circle |
| Circle | 2πr | r = radius of the circle |
| Trapezoid | Sum of all sides (a+b+c+d) | a, b, c, d being the lengths of the sides of the trapezoid. |
| Rhombus | 4a | a = side of the rhombus |
| Parallelogram | 2(a+b) | a = side of the parallelogram b = base of the parallelogram |
Read More: Lines and Angles
Things to Remember
- Area and Perimeter are two important concept used in the branch of mensuration.
- Area is measurement of amount of space occupied by any object.
- It is used to determine the space in the floor of a room.
- Perimeter is the measurement of the boundary within a shape enclosed.
- It can be calculated by tying a thread or string around the required object.
Read More:
Sample Questions
Ques: Find the perimeter of a square with the length of its one side 7 cm. (2 Marks)
Ans: Given, Length of the side, a = 7 cm
We know that, Perimeter of a square = 4a
Here, The perimeter of the square will be,
= 4a
= 4×7 cm
= 28 cm
Ques: Find the area of a square with the length of its one side 7 cm. (2 Marks)
Ans: Given, Length of the side, a = 7 cm
We know that, Area of a square = a²
Here, The area of the square will be,
= a²
= (7 cm)²
= 49 cm²
Ques: What will be the length of the sides of a square if the area of the square is 81 cm². (2 Marks)
Ans: Given, Area of the square = 81 cm²
We know that, Area of a square = a²
→ 81 cm² = a²
→ a = √81 cm²
→ a = 9 cm
Here, the length of the sides of the square is 9 cm.
Ques: The radius of a circle is 14 cm. Find the perimeter of the circle. (Take π=22/7) (2 Marks)
Ans: Given, Radius of the circle, r = 14 cm
We know that, Perimeter of a circle = 2πr
Here, The perimeter of the circle will be,
= 2πr
= 2 × 22/7 × 14 cm
= 2 × 22 × 2 cm
= 88 cm
Ques: The radius of a circle is 14 cm. Find the area of the circle. (Take π=22/7) (3 Marks)
Ans: Given, Radius of the circle, r = 14 cm
We know that, Area of a circle = πr²
Here, The area of the circle will be,
= πr²
= 22/7 × (14 cm)²
= 22/7 × 196 cm²
= 22 × 28 cm²
= 616 cm²
Ques: Find the area of a rectangle with length of 8 cm and width of 4 cm. (3 Marks)
Ans: Given,
Length = 8 cm
Width = 4 cm
We know that, Area of a rectangle = l×w
Here, The area of the rectangle will be,
= l×w
= (8 cm × 4 cm)
= 32 cm²
= 32 cm²
Ques: What will be the perimeter of a triangle with the side lengths of 3 cm, 6 cm and 9 cm. (3 Marks)
Ans: Given,
a = 3 cm
b = 6 cm
c = 9 cm
We know that, The perimeter of a triangle = a + b + c
Now, The perimeter of the given triangle will be,
= a + b + c
= (3 + 6 + 9) cm
= 18 cm
Ques: What will be the area of a triangle with the base length of 6 cm and height of 8 cm. (3 Marks)
Ans: Given,
b = 6 cm
h = 8 cm
We know that, The area of a triangle = ½ (b×h)
Now, The area of the given triangle will be,
= ½ (b×h)
= ½ (6×8) cm²
= ½ × 48 cm²
= 24 cm²
Ques: What will be the length of a rectangle if the perimeter and width of the rectangle is 48 cm and 8 cm respectively. (3 Marks)
Ans: Given,
Perimeter of the rectangle = 48 cm
Width of the rectangle (w) = 8 cm
We know that, Perimeter of a rectangle = 2 (l+w)
=> 48 = 2(l+8)
=> l+8 = 24
=> l = 24-8
=> l = 16 cm
So, the length of the rectangle is 16 cm.
Ques: Find the perimeter of a rectangle with length of 8 cm and width of 4 cm. (3 Marks)
Ans: Given,
Length = 8 cm
Width = 4 cm
We know that, Perimeter of a rectangle = 2 (l+w)
Here, The perimeter of the rectangle will be,
= 2(l+w)
= 2(8 cm + 4 cm)
= 2×12 cm
= 24 cm
Ques: What is the difference between area and perimeter of any geometric shape. (3 Marks)
Ans: The difference between the area an perimeter of any geometric shape is as follows:
| Area | Perimeter |
|---|---|
| Area is used to calculate the space occupied within the surface of a shape. | Perimeter is defined in the calculation of space ariund the boundary of an object. |
| It is expressed in terms of square units. | It is expressed in terms of unit. |
| The area of a rectangle is length x breadth. | The perimeter of a rectangle is 2 (length + breadth). |
Ques: A rectangular field has length 13 m and breadth 11 m. What will be the area as well as the perimeter of that field. (2 Marks)
Ans: Length of the rectangular field = 13 m
Breadth of the rectangular field = 11 m
Therefore, area of the field = l×b =13 × 11
=143 m2
And perimeter = 2(l+b) = 2(13+11)
=48m
Ques: If a rhombus has base and height 17 cm and 18 cm respectively, calculate its area. (2 Marks)
Ans: With regards to the question base = 17 cm
- Height = 8 cm
- Therefore, the area of rhombus =
- b×h
- 17 x 18
- 306 cm2
Ques: If the length of the side of a square is 15 cm. Then find its area and also find the total length of its boundary. (2 Marks)
Ans: Given, length of the side, a = 15 cm
Area = a2 = 152 = 225 sq.cm
Total length of its boundary,
Perimeter = 4a = 4 x 15 = 60 sq.cm.
Ques: The length of a rectangular carpet is 22 units. Its area is 484 square units. Find the width of the carpet and the perimeter of the carpet. (2 Marks)
Ans: Area of a rectangle = (length × width) square units.
- Given, length of the rectangular carpet = 22 units
- Area = 484 square units
- 22 × width = 484
- width = 484/22.
- Thus, the width of the rectangular carpet= 22 units.
Now,
- Perimeter of a rectangle = 2(length + width) units.
- Given: length of the rectangular carpet = 22 units
- Width of the rectangular carpet = 22 units.
- Substituting the values of length and width in the formula.
- Perimeter = 2 (22 + 22) = 2 (44) = 88 units.
- Therefore, the perimeter of the rectangular carpet = 88 units.
Ques: A circular-shaped garden has a radius of 30 units has to be fenced. Find the cost of fencing the circular garden if it takes $10 to fence one unit. (Use the value of π as 22/7) (3 Marks)
Ans: To calculate the cost of fencing the garden, we first have to find the outer boundary length of the garden.
- To find that let us find the perimeter of the circular garden with a radius of 50 units.
- For a circle, the circumference = 2πr units.
- Given: radius = 30 units.
- Therefore, circumference = 2 × (22/7) × 30 = 188.571 units.
- The cost of fencing 1 unit of the garden = $10.
- Therefore, the cost of fencing 188.571 units of the garden = 188.571 × 10 = $1885.71
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments