
Namrata Das Exams Prep Master
Exams Prep Master
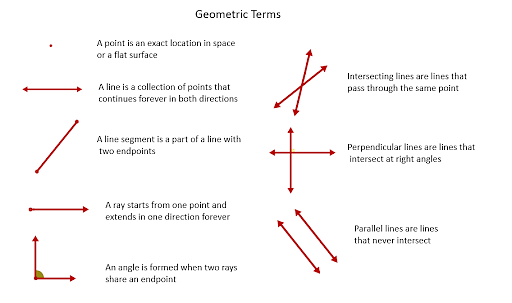
Lines And Angles are considered to be the basic shapes in geometry. Geometry is the study of a figure's various shapes, sizes, spaces, and relative positions. They are all made up of points, lines, and angles, which allow them to easily define their structures and areas. In geometry, a point is something that has no components. It is symbolized by a dot. A line is formed when two distinct points are joined. Because there are no endpoints on a line, it can be extended indefinitely. Line Segment is the section of a line that has two endpoints. Ray is also a part of the line that has only one endpoint and no other end. An angle is a figure where two rays emerge from a common point. Here, we will be learning more about lines and angles and discuss some important questions.
| Table of Content |
Key takeaways: Lines, Angles, Types, Properties
Also read: Isosceles Triangle Theorems
What are Lines?
[Click Here for Sample Questions]
Lines are defined as a set of infinitesimally small points. A line with two arrowheads can be extended in either direction. A segment, on the other hand, is a defined finite space between two points. It is not possible to extend it in either direction. It's a subset of the line that's used to calculate its length. It has been observed that students frequently mix up lines and segments. The primary distinction between lines and segments is that the former can be extended, whereas the latter has a fixed length. This distinction can be seen in the chapter on class 3 lines and point angles.
Types of Lines
Vertical line: It is a line that exists on the vertical plane. In terms of orientation, it runs from north to south. To put it simply, it is a line that runs from the top of the page to the bottom of the page.
Horizontal line: It is a line that exists on the horizontal plane. In terms of orientation, it runs from East to West. Simply put, it is a line that runs from the left to the right side of the page.
Parallel Line: A parallel line is formed when two lines run in the same direction without intersecting or meeting. These lines can be extended indefinitely, but they will never meet.
Perpendicular Line: When two straight lines intersect at a 90-degree angle, they are said to be perpendicular to each other. Their angle is also referred to as a right angle. Their point of intersection is the point at which they intersect. At the intersection of two perpendicular lines, four right angles are formed.
Also Read:
What are Rays?
[Click Here for Sample Questions]
A Ray is similar to a line but has a fixed beginning point and can only be extended infinitely in one direction. Rays are essential in the introduction to angles.
Read More:
What are Angles?
[Click Here for Sample Questions]
An angle is a space formed by two rays with the same vertex. The two rays can be extended in the direction indicated by the pointed arrow at their ends.
Types of Angle
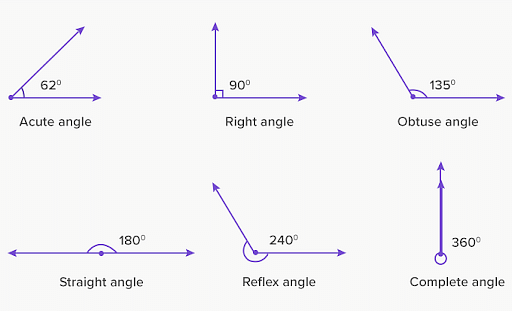
An angle can be of various types depending on its application. Here are a few examples:
Acute Angle: An acute angle is formed by two rays that are 0° to 90° apart. The angle value is never greater than 90°.
Right angle: is formed by two perpendicular rays intersecting each other. This angle is always measured as 90°.
Obtuse Angle: This is an angle formed by two rays that are 90° to 180° apart. This angle's measure is always greater than 90°.
Some other types of angles are
Straight Angle: An angle with a measurement of 180°. It appears to be a straight line with both arms pointing in opposite directions.
Reflex Angle: A type of angle whose value is always the greater of two possible angles formed by a pair of rays. It has a range of 180° to 360°.
Complete Angle: An angle that completes one turn in either a clockwise or anti-clockwise direction or returns to its starting position. This angle has a measurement of 360°.
Read More:
Properties of Lines and Angles
[Click Here for Sample Questions]
Pairs of Angles Axioms
- If a ray is perpendicular to a line, the sum of two adjacent angles formed by that ray is 180°.
This demonstrates that the common arm of the two angles is the ray standing on a line, and the two adjacent angles are the angles' linear pair. Because the sum of two angles is 180°, these are also supplementary angles.
- If the sum of two adjacent angles is 180°, then the arms of the angles that are not common form a line.
This contradicts the first axiom, which states that the inverse is also true.
Theorem of Vertically Opposite Angles
When two lines intersect, the vertically opposite angles that result are equal.
Angles that are vertically opposed
Because AC and BD are intersecting, AOD = BOC and AOB = DOC.
Parallel Lines and a Cross-Section
When a line passes through two distinct lines and intersects them at different points, this line is referred to as a transversal line.
When a transversal intersects two lines, two angles are formed.
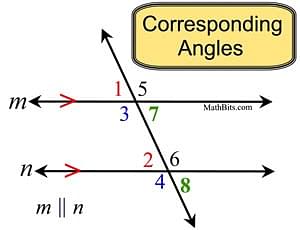
- Corresponding Angles :
- ∠ 1 and ∠ 5
- ∠ 2 and ∠ 6
- ∠ 4 and ∠ 8
- ∠ 3 and ∠ 7
- Alternate Interior Angles :
- ∠ 4 and ∠ 6
- ∠ 3 and ∠ 5
- Alternate Exterior Angles:
- ∠ 1 and ∠ 7
- ∠ 2 and ∠ 8
- Interior Angles on the same side of the transversal:
- ∠ 4 and ∠ 5
- ∠ 3 and ∠ 6
Axioms of Transversality
- Axioms of Transversality
- When a transversal intersects two parallel lines, it is said to be a transversal.
- Each corresponding angle pair will be equal.
- Each alternate interior angle pair will be equal.
- Each supplementary pair of interior angles on the same side of the transversal.
- If a transversal intersects two lines such that:
- If the corresponding angles are equal, these two lines will be parallel.
- When the alternate interior angles are equal, the two lines are parallel.
- When interior angles on the same side of the transversal are supplementary, the two lines become parallel.
Read More:
Angle Sum Property of a Triangle
[Click Here for Sample Questions]
- The sum of the angles of a triangle is 180º.
∠A + ∠B + ∠C = 180°
- If we produce any side of a triangle, then the exterior angle formed is equal to the sum of the two interior opposite angles.
∠BCD = ∠BAC + ∠ABC
Read More:
Things to Remember
- A vertical line is a line that exists in the vertical plane i.e., it runs from north to south. A horizontal line is a line that exists in the horizontal plane i.e., it runs from East to West.
- A parallel line is formed when two lines run in the same direction without intersecting or meeting.
- When two straight lines intersect at a 90-degree angle, they are said to be perpendicular to each other. Their angle is also referred to as a right angle.
- Ray has a fixed beginning point and can only be extended in one direction. It is essential in the introduction to angles.
- An angle is a space formed by two rays with the same vertex.
Also Read:
Sample Questions
Ques: What is the difference between Complementary and Supplementary Angles? (3 marks)
Ans: Complementary angles are defined as the sum of two angles that add up to 90°. For example, if one angle has a measure of 50°, its complement angle would be 90° - 50° = 40°. Thus, if one angle's measurement is known, the value of the other can be easily calculated by subtracting the known angle from 90°.
A supplementary angle is a pair of angles whose sum equals 180°. So, if one angle's measurement is known, the value of the other can be calculated by subtracting the known angle from 180°.
Ques: What are the definitions of Adjacent and Vertically Opposite Angles? (3 marks)
Ans: The term "adjacent angles" refers to a pair of angles that share the same vertex and one arm. The adjacent angles are next to each other. As a result, when being measured, they should not overlap. They can share the vertex equally or be complementary to one another.
Angles with the same vertex but placed exactly opposite to each other are called vertically opposite angles. They are made up of the same two intersecting lines. Because they are mirror images of one another, their angles are always equal.
Ques: Find ∠DGH. (2 marks)
Ans: Here, AB \(\parallel\) CD and EH is transversal.
∠EFB + ∠BFG = 180° (Linear pair)
∠BFG = 180°- 133°
∠BFG = 47°
∠BFG =∠DGH (Corresponding Angles)
∠DGH = 47°
Ques: Find x and y. (5 marks)
Ans: Here, ∠A + ∠B + ∠C = 180° (Angle sum property)
30°+ 42° + x = 180°
x = 180°- (30° + 42°)
x = 108°
And y is the exterior angle and the two opposite angles are ∠A and ∠B.
So,
∠BCD = ∠A + ∠B (Exterior angle is equal to the sum of the two interior opposite angles).
y = 30°+ 42°
y = 72°
We can also find it by linear pair axiom as BC is a ray on the line AD, so
x + y = 180°.
Also Check:





Comments