Triangle Inequality Theorem: Mechanism and Proof

A triangle is a two-dimensional shape that has three sides with three vertices. The three sides of a triangle may or may not have equal sides. Triangles are typically classified into three different types, broadly named as equilateral, isosceles and scalene triangles. The triangle inequality theorem is a vital topic that is widely used in matters concerning surveying, transportation, and even civic layouts. It helps in determining the relationship between the three sides of a triangle.

---

Triangle Inequality Theorem

The Triangle Inequality Theorem, as the name suggests, explains the relationship between the three sides of a triangle. 

Typically, this theorem helps in estimating the unspecified lengths of a triangle, alongside giving a brief evaluation of multiple dimensions. The triangle inequality theorem mentions that to form a triangle, the sum of two sides in it has to be greater than the third one.

In simple words, this theorem proves that the shortest distance between two individual points always results in a straight line.

On a brief note, the triangle inequality theorem is a very useful mechanism to check whether or not a group of three dimensions will supposedly form a triangle. If put simply, if the conditions tend to become false on its own, seemingly when the sum of two sides of a triangle are less than the third side, then the triangle will not form. One of the typical places the triangle inequality theorem is utilized widely is on online map applications, like Google maps, to estimate the lengths between unknown distances.

This image is an example of how the inequality theorem of a triangle is made effective.

In accordance with the Triangle Inequality theorem,

• AB + BC is greater than AC, or AB + BC > AC.
• AB + AC is greater than BC, or AB + AC > BC
• BC + AC is greater than AB, or BC + AC > AB.

Also Read:

Triangle Inequality Theorem Mechanism 

Consider an example where you are given to walk along the sides of a triangle. Now, if you are directed to go from A to B, then the shortest path will definitely be the AB segment. However, if you walk to C first and then consequently go to B, then wrapping up, the distance becomes AC + CB, which is multiple times greater than the distance covered prior.

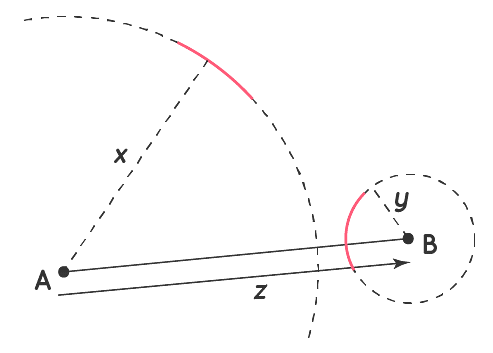
Now, watch the image carefully. According to the Inequality Theorem, the two arcs that are formed using a compass have to intersect one another, only if the sum of the two arcs’ radii is greater than the distance covered between the arc’s center space. 

To put simply, x + y will have to be greater than z to further form a triangle. In any case whatsoever, the triangle cannot have two sides of the measurement 2, with the third side typically being 5 or more. This is because 2 + 2 = 4 is less than 5 and more.

This is the working mechanism of the inequality theorem of a triangle.

Also Read:

Proof of Triangle Inequality Theorem

To explain the proof behind the inequality theorem, imagine a triangle ?ABC that has three sides; a, b and c.

Now, as per what the triangle inequality theorem claims,

a < b + c,

b < a + c,

c < a + b.

Now, according to the statement asserted above, the shortest distance that can be evidently seen from any vertex to the opposite side of the triangle is typically considered as the perpendicular. Now, as per what is shown below, XP is known to be the shortest line segment from point (vertex) X to the side of YZ.

Now look at the figure exhibited below to understand the theorem,

Theorem to Prove: |BC|< |AB| + |AC|

As per the image, we need to extend the side BA to the point D such that AD = AC. Now, after extending the line segment, we need to join C to D.

It becomes important to consider that ∠ACD = ∠D, which implied that in  ?BCD, ∠BCD > ∠D. Typically, larger angles tend to make larger distances, which is to say, BD > BC

Therefore, AB + AD > BC

AB + AC > BC (since, AD = AC)

This proves that since the sum of two sides is greater than the third, it is possible to form a triangle. Hence, the triangle inequality theorem is proved.

---

Things to Remember

1. The Triangle Inequality Theorem simply helps in explaining the relationship between the three sides of a triangle. 
2. The triangle inequality theorem mentions that the sum of two sides in any triangle is greater than the third one.
3. AB + BC is greater than AC, or AB + BC > AC; AB + AC is greater than BC, or AB + AC > BC; BC + AC has to be greater than AB, or, BC + AC > AB.
4. For a triangle to form, two arcs have to intersect with the condition that the sum of the radii of the two arcs is typically greater than the distance covered between the arc’s center space.
5. The triangle inequality theorem clearly mentions that |BC|< |AB| + |AC|.

Also Read:

---