How to Calculate Percentage: Formula, Basic Tricks, Solved Examples

Percentage in mathematics is a ratio or number to measure the proportion of value, where the value is always 100. Various methods have been introduced on how to calculate percentage increase, decrease, difference, etc. For example, in profit or loss, percentage is widely used in businesses and institutions to represent marks. For example, Jack scored 40% marks in English, which means he scored 40 marks out of 100. In terms of fraction, it can be written as 40/100 and in terms of ratio, it can be written as 40:100.

Also read: Ratio to Percentage

Key Terms: Percentage formula, Percentage calculator, Increase formula, Decrease formula, Fraction, Ratio

---

What is Percentage?

[Click Here for Sample Questions]

Percentage is defined as an amount or part in every hundred. In percentage,100 is always the denominator and it is represented by the symbol ‘%’. Percentage is called a dimensionless number as they have no dimension. Percentage can also be further represented as simple fractions or decimal fractions. 

For example, when we say 60% of one number, then it means 60 percent of its whole.

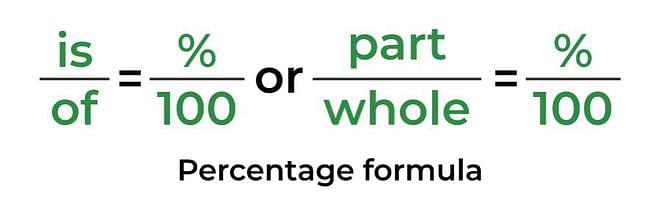
Percentage

Read More: Real Number System

---

How to Calculate Percentage?

[Click Here for Sample Questions]

To calculate percentage means to find out the whole number in terms of 100. Hence the formula to calculate percentage is:

P% of a Number = X

Here, X is the required percentage

We can express the above formula as mentioned below after removing the % sign

P/100 x Number = X

For Example:

Let 10% of 40 = X

10/100 * 40 = X

X = 4

However, there are two ways to calculate percentage:

• Using the unitary method.
• Changing the fraction’s denominator to 100.

Percentage Formula

Percentage formula determines the share of a whole in terms of hundreds. This formula helps to represent a number as a fraction of 100. Percentage formula can be obtained by dividing the given value by the total value and then multiplying the rest with 100 as shown below:

(Value/Total value) × 100

How to calculate percentage using above formua with an example:

Let’s Assume: 50% of a number is 360. What will be 90% of the same number?

Let the number be y.

50/100 × q = 360

i.e q = 720

90% of 720

90/100 × 720

= 648

How to Calculate Percentage: Basic Trick

The following trick can be used to calculate the percentage:

X % of y = y % of x

For example, Prove 10% of 40 is equal to 40% of 10

Solution:

10% of 40 = 4

40% of 10 = 4

Therefore, we can say that these are equal, and hence we can also write,

x % of y = y % of x

The percentage formula in the case of the fraction is shown below:

Numerator/ Denominator x 100

Also Read:

---

How to Calculate Percentage Increase?

[Click Here for Sample Questions]

Percentage increase is the difference between final value and initial value. Following this concept, percentage increase formula is derived and expressed as:

Percentage Increase = [(Final Value - Initial Value)/Initial Value] × 100

Note: Since percentage has to be a positive quantity, absolute value of the initial value is taken.

Percentage increase formula applies when compared to the original value, the new value is greater. Percentage change in value indicates an increase of percentage in the original number, for example,

Percentage increase = (Increase in value/ original value) x 100

Here, Increase in value = New value – original value

Let us learn how to calculate percentage increase with an example:

Height of a tree increased from 10 ft to 20 ft after a year. Find the percentage increase in its height.

Solution: Initial height of the tree = 10 ft.; Final height of the tree = 20 ft.

Using percentage increase formula,

Percentage Increase = [(Final Value - Initial Value)/Initial Value] × 100

= [(20 - 10)/10)] × 100 = (10 /10) × 100

= 100%

Thus, percentage increase in height of the tree = 100%.

---

How to Calculate Percentage Decrease?

[Click Here for Sample Questions]

Percentage decrease formula applies when compared to the original value, the new value is lesser. Percentage change in value indicates a decrease of percentage in the original number, for example,

Percentage decrease = Decrease in value/ original value x 100

Here, decrease in value = Original value- New value

Let us learn how to calculate percentage decrease with an example:

The number 65 is misread as 56. Calculate percentage decrease using the percent decrease formula.

Solution: New value = 56 and old value = 65

Using the Percentage Decrease formula, we get

Percent Decrease = [(Old Value - New Value) / Old Value] × 100

= [(65 - 56) / 65] × 100

= 9/65 × 100

= 13.84%

Thus, percent decrease of the number is approximately 14%

Read about: Sequence and Series

---

How to Calculate Percentage of Marks?

[Click Here for Sample Questions]

Calculation of percentage of marks is required during or after exams to determine the marks obtained by a student against the total marks. This is calculated through two steps:

• Total marks are divided by Maximum marks 
• The result value is multiplied by 100

Percentage of Marks = (Marks Obtained / Total Marks) x 100

Let us learn how to calculate percentage decrease with an example:

A student obtained 60 marks in an examination with total marks as 100. Calculate the percentage of marks scored by the student.

Solution: Number of marks scored = 60

Maximum marks = 100

Percentage of marks = (Marks obtained/Total marks) × 100

Percentage = (60 / 100) × 100 = 60%

Thus, percentage of marks obtained is 60%

---

How to Calculate Percentage of Sales?

[Click Here for Sample Questions]

Method of calculation of percentage of sales is also termed as Percentage of Sales Method used by business owners and/or employees who create budgets. This method determines the ratio of expenses to sales. High ratios may lead to adjustments that would reduce the expense percentage and increase profits. 

Percentage of Sales can be calculated in 3 steps:

Step 1: Determine expenses and total sales for the period

Step 2: Divide expenses by total sales

Step 3: Multiply the output by 100

Percentage of Sales = (Expenses / Sales) x 100

Let us learn how to calculate percentage of sales with an example:

Expenses of XYZ including costs of goods sold is $5,000 per year. While the Revenue is $20,000 per year. Calculate the percentage of sales.

Solution: Expenses: $5,000 and Revenue: $20,000

Percentage of Sales = (Expenses / Sales) x 100 

Percentage = 5,000 / 20,000 = 0.25

Percentage = 0.25 x 100 = 25

Thus, 25% of sales revenue goes to the costs of goods sold account. 

---

Things to Remember

• Percentage means a ratio or number to measure the proportion of value, where the value is always 100.
• Percentage calculation means to find out the whole number in terms of 100.
• Percentage formula is P% of a Number = X
• Percentage formula is (Value/Total value)×100
• The basic percentage trick is X % of y= y % of x
• Percentage formula in case of friction is Numerator/Denominator x 100
• Percentage increase formula is Percentage increase = Increase in value/ original value x 100
• Percentage decrease formula is Percentage decrease = Decrease in value/ original value x 100

Also Read: