
Collegedunia Team Content Curator
Content Curator
Area and perimeter are the fundamental concepts in geometry used for measurement. Area is the extent of a two-dimensional figure whereas Perimeter is the measurement of the outer boundary of the two-dimensional figure. These parameters are extensively used to calculate the dimensions and properties of a given geometry. It is also used in many real-life applications like land surveying, aerial and urban planning.
Keyterms: Area, Perimeter, Geometry, Measurement, Dimension, Meter, Triangle, Square
Read More: Surface areas
Area
Area is the range of a specific region occupied by a two-dimensional geometric figure. Usually, in the SI system, the area is measured in meter square(m²). To understand the concept of an area, think about a stadium. Here, the area is the entire space where the players can play. Now to calculate the area, determine the shape of the area and use the appropriate formula.
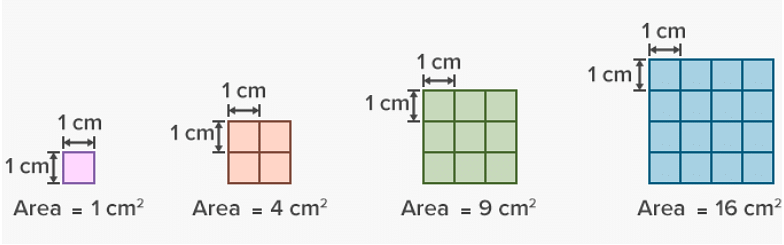
Area
Also Read:
Area Formula
The area formula for different geometric figures is tabulated below.
| Geometric figures | Formula of area |
|---|---|
| Triangle | ½ x b x h [b=base, h=height] |
| Square | a² [a=side of a square] |
| Rectangular | l x b [l=length, b=width] |
| Circle | x (r)² [r=radius] |
| Semicircle | ½ x x (r)² |
| Rhombus | a x h [a=side, h=height] |
| Parallelogram | b x h [b=base, h=height] |
| Trapezium | ½ x (a+b) x h [a=upper base of parallel side, b=lower base of parallel side, h=height] |
Also Read:
Perimeter
Perimeter is the boundary of two-dimensional closed path shapes. Perimeter mainly is the enclosed boundary or the sum of all the sides of a geometric figure. The unit used for Perimeter is meter(m).
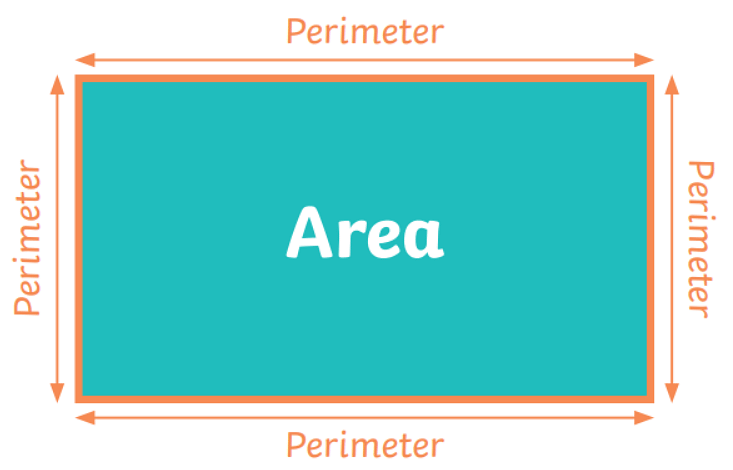
Perimeter
Bringing the previous example, if the question is about the perimeter of the circled cricket ground, you only need to calculate the value of the outline of the ground.
Also Read: Section Formula
Perimeter Formula
The perimeter formula for different geometric figures are tabulated below.
| Geometric figures | Formula of Perimeter |
|---|---|
| Triangle | 3a [a=side] |
| Square | 4a [a=side] |
| Rectangular | 2(l+b) [l=length, b=width] |
| Circle | 2 x x r [r=radius] |
| Semicircle | x r + 2 x r [r=radius] |
| Rhombus | 4a [a=side of a rhombus] |
| Parallelogram | 2(b+a) [b=parallel base, a=side of parallelogram] |
| Trapezium | 4a [a=side] |
Also Read:
Difference between Area and Perimeter
The key differences between area and perimeter are tabulated below.
| Parameters | Area | Perimeter |
|---|---|---|
| Definition | Area is the range of space occupied by an enclosed two-dimensional geometric figure. | Perimeter is the length of the outline that encloses any two-dimensional geometric figure. |
| Unit | The area is measured in square units. ( Square meter - m²) | Perimeter is measured in linear units. (Meter - m) |
| Space | Area is the internal space of a geometric figure or shape. | Perimeter is the outline or boundary of a shape. |
| Example | Area of a circular cricket ground in stadium | The fence of farming land. |
Also Read: Nature of Roots of Quadratic Equation
Things to Remember
- Area is the region that is occupied under any kind of two-dimensional geometric shape.
- The units of area are expressed in terms of meter square or centimetre square.
- Perimeter is the outer boundary of any geometric shape.
- The unit of the perimeter is linear.
Also Read:
Sample Questions
Ques: Find out the area and perimeter of a rectangle whose length is 24 meters and width is 7 meters. [2 marks]
Ans: Given, the length of the rectangular= 24 meter
The width of the rectangular= 7 meter
∴ The area of the rectangle= length width= 24 7 = 168 m²
Ques: Write down the difference between Area and Perimeter. [3 marks]
Ans:
| Area | Perimeter |
|---|---|
| Area is the range of space occupied by an enclosed two-dimensional geometric figure. | Perimeter is the length of the outline that encloses any two-dimensional geometric figure. |
| The area is measured in square units. ( Square meter - m²) | Perimeter is measured in linear units. (Meter - m) |
| Area is the internal space of a geometric figure or shape. | Perimeter is the outline or boundary of a shape. |
| Area of a circular cricket ground in stadium | The fence of farming land. |
Ques: What is an area in geometry? Write down the formula of area for circle and parallelogram. [3 marks]
Ans: Area is the range of a specific region occupied by two-dimensional geometric figures.
The area of circle= x (radius)²
The area of parallelogram= base x height
Ques: What is Perimeter in geometry? Write down the perimeter of the semicircle and square. [3 marks]
Ans: Perimeter is the outline which encloses the boundary or the sum of all the sides of a one or two-dimensional geometric figure.
The perimeter of the semicircle is x radius + 2 x radius.
The perimeter of the square is 4 x side.
Ques: What is the perimeter or circumference of a circle of diameter of 20 meter. Calculate the area of the circle. [2 marks]
Ans: The diameter of the circle= 20 meter
∴ The radius(r) = 20/2 = 10 meter
∴ The perimeter of the circle = 2r= 210 meter = 62.83 m
Also Read:
Ques: A circle is formed using a ribbon which has a radius of 28 cm. Let’s say Rohan wants to form a square using the same ribbon, determine the length of the side of the square formed by Rohan using the ribbon. [4 marks]
Ans: The radius of the circle= 28 cm
Now, since the circle is formed using ribbon,
∴ length of the ribbon = the perimeter of the circle
∴ The length of the ribbon = 2r=(2x 28) cm
And again the ribbon will form the square of 4 sides.
Hence, 4side=(2x 28)
∴ The side of the square=2284= 43.98 cm
Ques: A rectangle ground has a width that is thrice of its length. If the length is 128 cm, what will be the cost of fencing the rectangle at a cost of 20 rupees per square meter. [3 marks]
Ans: The length of the rectangular place= 128 cm
Given, Width = 3length= 3128 cm = 384 cm
∴The area of the rectangular place = 384128 = 49152 cm² = 49152/100 meter² = 491.52 meter square
Now, 1 square meter costs 20 rupees to fence.
∴491.52 square meter will cost= 491.52 20= 9830.4 rupees to fence.
Ques: A lawn that has 400 cm length and 138 cm width needs to be covered with tiles. How many tiles with dimensions 5 cm X 12 cm will be needed to cover the lawn. [3 marks]
Ans: The length of the lawn= 400 cm
The width of lawn= 138 cm
∴The area of the lawn= 400 x 138 = 55200 cm²
A tile of dimension 5 cm x 12 cm can cover= 5 x 12 = 60 cm² of area.
∴The lawn needs = 55200/60 = 920 tiles to cover it.
Also Read: Triangles Important Questions Class 10
Ques: Find the perimeter and area of the semi-circle below. [3 marks]

Ans: The diameter of the semi circle= 14 cm
∴The radius = 14/2 = 7 cm
∴The perimeter of the semi circle= r+2r= 22/7 x 7 + 2 x 7 = 36 cm
∴The area of the semi circle= ½ x x r² = ½ x 22/7 x 7 x 7=77 cm²
Ques: Find out the area and perimeter of a rectangle whose length is 56 meters and width is 30 meters. [2 marks]
Ans: Given, the length of the rectangular= 56 meter
The width of the rectangular= 30 meter
∴ The area of the rectangle= length width= 5630 = 1680 m²
Perimeter = 2(l+b)
Perimeter = 2 (56 + 30)
Perimeter = 172 m
Also Read:






Comments