Isosceles Triangle Theorems: Proof and Sample Questions

Jasmine Grover Content Strategy Manager

Content Strategy Manager

An isosceles triangle is a type of triangle which has two sides with equal lengths. Based on the length of the sides, there are two types of triangles- Equilateral and Isosceles. While isosceles triangles have two sides equal, all sides are equal in an equilateral triangle. To have a better understanding of the properties of an isosceles triangle, there are two main theorems called the isosceles triangle theorems. These theorems are used to solve mathematical problems related to the sides and the angles of an isosceles triangle. In this article, we will look at the isosceles triangle theorems, their proof, and related sample questions.

Table of Contents

What is an isosceles triangle?
Isosceles triangle theorems
Things to Remember
Sample Questions

Keywords: Isosceles triangle, Equal angles, acute angles, isosceles triangle theorems, congruent triangles

What is an isosceles triangle?

A triangle that has two sides of equal lengths is called an isosceles triangle.

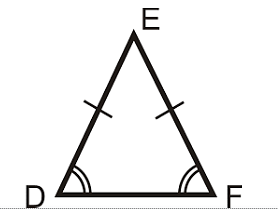
Properties of an Isosceles Triangle

Considering the given,ΔEDF:-

It has two equal sides i.e., ED=EF.
It has two equal angles that are the base angles (∠EDF and ∠EFD)
All the angles are acute i.e., their measure is less than 90°.
If the third angle is 90°, then it is known as a right isosceles triangle.

Isosceles triangle theorems

The theorems for an isosceles triangle along with their proofs are as follows;

Theorem 1: The angles opposite to the equal sides of an isosceles triangle are also equal.

Proof: Let us consider a ΔABC,;

Given: AB=BC

To prove: Angles opposite to the sides AB & BC are equal i.e., ∠ABC=∠ACD

⇒ To prove the above statement, we first draw a bisector that intersects the base at point D.

Now,

In ΔBAD and ΔCAD,

AB = BC (Given condition)

∠BAD = ∠DAC (By construction);

AD = AD (Common to both the triangles)

Therefore, ΔBAD ≅ ΔCAD by SAS congruency criterion.

Hence, ∠ABC = ∠ACD (by CPCT);

In conclusion, ∠ABC and ∠ACD are the congruent parts of the congruent triangles, ΔBAD and ΔCAD. Therefore, the angles ABC and ACD opposite to the sides AC and AB respectively, are equal.

Theorem 2: The sides opposite to the equal angles of an isosceles triangle are equal.

Proof: This theorem is the converse of theorem-1.

Now, it is given that the base angles are equal or ∠ABD = ∠ACD.

We have to prove that the sides opposite to these angles are equal i.e., AB = AC.

For this, we first construct a bisector that meets the base BC at right angles.

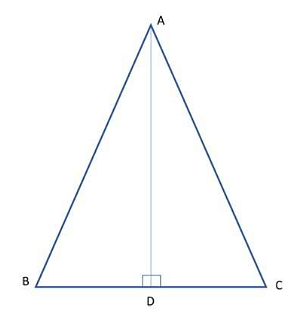
⇒ In ΔABD and ΔADC,

∠ABD = ∠ACD (Given)

AD = AD (Common to both triangles)

∠ADB = ∠ADC = 90°

Thus, ΔABD ≅ ΔADC by ASA congruency criterion.

Hence, by CPCT, AB = AC.

Therefore, the sides AB & AC which are opposite to the angles ∠ACD and ∠ABD respectively, are equal since they are the congruent parts of the congruent triangles ΔABD and ΔADC.

Things to remember

An isosceles triangle has two equal sides.;
All the interior angles are acute.
The sides opposite to the equal angles in an isosceles triangle are equal.
The angles opposite to the equal sides in an isosceles triangle are equal.

Sample Questions

Ques. In a triangle, one angle measures 70° and the other two angles are equal. What are the values of the other two angles? (5 marks)

Ans. Let the angles of the given triangle be ∠A, ∠B, and ∠C.

It is given that ∠A = 70°.

Since, ∠B and ∠C are equal, then it must be an isosceles triangle.

According to the angle-sum property of a triangle, the sum of all the angles would be 180°.

Hence, ∠A +∠B + ∠C= 180°.

70° + x + x = 180°

70° + 2x = 180°

2x = 180° – 70°

2x = 110°

x = 110/2

x = 55°

∴ ∠B = ∠C = x = 55°

Hence, the measure of the other two angles ∠B and ∠C are equal and is 55°.

Ques. In the given figure, find the value of angles x and y. (5 marks)

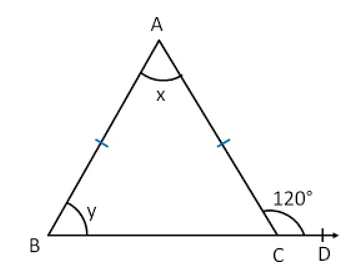
Ans. In the given ΔABC, AB = AC, ∴ it is an isosceles triangle.

According to the isosceles triangle theorem, angles opposite to equal sides are also equal. Therefore, ∠ABC = ∠ACB = y,

Now, ∠ACB + 120° = 180° since, ∠ACB and ∠ACD make a linear pair.

y + 120° = 180°

y = 180° – 120°

y = 60°

∠ABC = ∠ACB = 60°

Now, in ΔABC,

According to the angle-sum property of a triangle,

∠ABC + ∠ACB + ∠BAC = 180°

y + y + x = 180°

2y + x = 180°

x = 180° – 2y

x = 180° – (2 x 60°)

x = 180° – 120°

x = 60°

Hence, x = 60° and y = 60°

Ques. Find the value of ‘y’, when it is given that the following triangle is isosceles. (3 marks)

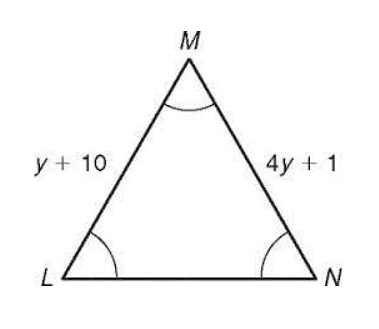
Ans. Since ΔMLN is an isosceles triangle, we can assume that ML = MN as the two sides of an isosceles triangle is equal.

ML = MN

y + 10 = 4y + 1

10 – 1 = 4y – y

9 = 3y

3y = 9

y = 3

Hence, the value of y is 3.

Ques. What are the values of ∠BCA and ∠ABC in the following figure? (5 marks)

Ans. Since in ΔBAC, it is given that AB = BC, therefore, it is an isosceles triangle.

Following the isosceles triangle theorem i.e., the angles opposite to the equal sides of an isosceles triangle are also equal, we get, ∠BAC = ∠BCA.

∴ y = ∠BCA = 52°

Now, according to the angle-sum property of a triangle,

∠BAC + ∠BCA + ∠ABC = 180°

52° + 52° + (14x+6) ° = 180°

104° + 14x + 6 = 180°

14x + 110° = 180°

14x = 180° – 110°

14x = 70°

x = 70/14 = 5°

∴∠ABC = 14x+6 = (14 x 5) + 6 = 70 + 6 = 76°

Hence, ∠BCA = 52° and ∠ABC = 76°

Ques. Find the perimeter of ΔABC, where AB = 4.5cm and BC = 3.2 cm given that it is an isosceles triangle. (3 marks)

Ans. Given- AB = 4.5cm and BC = 3.2cm

Since, ΔABC is an isosceles triangle, therefore, AB = AC = 4.5cm

Thus, Perimeter of ΔABC = AB + BC + AC

4.5 + 4.5 + 3.2
12.2 cm

Hence, the perimeter of ΔABC is 12.2 cm.

Ques. The perimeter of the given triangle is 64cm. Find the lengths of all the sides and also state which type of triangle it is. (5 marks)

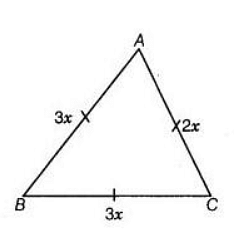
Ans. Perimeter of a triangle = Sum of all of its sides

∴ Perimeter of ΔABC = AB + BC + AC

3x + 3x + 2x = 64cm
8x = 64cm
x = 64/8 = 8cm

AB = 3x = 3 x 8 = 24cm

BC = 3x = 3 x 8 = 24cm

AC = 2x = 2 x 8 = 16cm

Thus, the lengths of the sides AB, BC, and AC are 24cm, 24cm, and 16cm respectively.

Also, since AB = BC = 24cm, two sides of the triangle are equal. Hence, ΔABC is an isosceles triangle.

Ques. What is the value of ‘x’ and ‘y’ in the given figure? (5 marks)

Ans. In the given figure, ∠BAC = 80° since they are Vertically opposite angles.

Since ΔABC is an isosceles triangle, ∠ABC = ∠ACB (Angles opposite to equal sides are also equal).

Applying angle-sum property in ΔABC, we get

∠ABC + ∠ACB + ∠BAC = 180°

x + x + 80° = 180°

2x = 180° – 80°

2x = 100°

x = 50°

Now, ∠ACB + y = 180° (Linear Pair)

y = 180° – 50° = 130°

Hence, x = 50° and y = 130°;

Ques. Find the value of ‘x’ in the given figures: (5 marks)
(1)
(2)

Ans. Since AB = BC, therefore, ΔABC is an isosceles triangle.

Also, the angles opposite the equal sides of an isosceles triangle are equal.;

So, ∠BAC = ∠BCA = 72°

Applying angle-sum property to ΔABC,

∠BAC + ∠BCA + ∠ABC = 180°

72° + 72° + x = 180°

144° + x = 180°

x = 36°

Thus, x = 36°

Since ∠ABC and ∠ACB are equal, therefore, ΔABC is an isosceles triangle.

According to the isosceles triangle theorem, the sides opposite to equal base angles are also equal.

∴ AB = BC

Thus, x = 16cm.

Isosceles Triangle Theorems: Proof and Sample Questions

What is an isosceles triangle?

Properties of an Isosceles Triangle

Isosceles triangle theorems

Things to remember

Sample Questions

CBSE X Related Questions

1.
\(\alpha, \beta\) are zeroes of the polynomial \(3x^2 - 8x + k\). Find the value of \(k\), if \(\alpha^2 + \beta^2 = \dfrac{40}{9}\)

2.
In a right triangle ABC, right-angled at A, if $\sin B = \dfrac{1}{4}$, then the value of $\sec B$ is

3.
Prove that \(\dfrac{\sin \theta}{1 + \cos \theta} + \dfrac{1 + \cos \theta}{\sin \theta} = 2\csc \theta\)

4.
Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

5.
Let $p$, $q$ and $r$ be three distinct prime numbers. Check whether $pqr + q$ is a composite number or not. Further, give an example for three distinct primes $p$, $q$, $r$ such that
(i) $pqr + 1$ is a composite number
(ii) $pqr + 1$ is a prime number

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

Isosceles Triangle Theorems: Proof and Sample Questions

What is an isosceles triangle?

Properties of an Isosceles Triangle

Isosceles triangle theorems

Things to remember

Sample Questions

CBSE X Related Questions

1.\(\alpha, \beta\) are zeroes of the polynomial \(3x^2 - 8x + k\). Find the value of \(k\), if \(\alpha^2 + \beta^2 = \dfrac{40}{9}\)

2.In a right triangle ABC, right-angled at A, if $\sin B = \dfrac{1}{4}$, then the value of $\sec B$ is

3.Prove that \(\dfrac{\sin \theta}{1 + \cos \theta} + \dfrac{1 + \cos \theta}{\sin \theta} = 2\csc \theta\)

4.Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

5.Let $p$, $q$ and $r$ be three distinct prime numbers. Check whether $pqr + q$ is a composite number or not. Further, give an example for three distinct primes $p$, $q$, $r$ such that (i) $pqr + 1$ is a composite number (ii) $pqr + 1$ is a prime number

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

1.
\(\alpha, \beta\) are zeroes of the polynomial \(3x^2 - 8x + k\). Find the value of \(k\), if \(\alpha^2 + \beta^2 = \dfrac{40}{9}\)

2.
In a right triangle ABC, right-angled at A, if $\sin B = \dfrac{1}{4}$, then the value of $\sec B$ is

3.
Prove that \(\dfrac{\sin \theta}{1 + \cos \theta} + \dfrac{1 + \cos \theta}{\sin \theta} = 2\csc \theta\)

4.
Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

5.
Let $p$, $q$ and $r$ be three distinct prime numbers. Check whether $pqr + q$ is a composite number or not. Further, give an example for three distinct primes $p$, $q$, $r$ such that
(i) $pqr + 1$ is a composite number
(ii) $pqr + 1$ is a prime number