
Content Curator
Collinear points are three or more points that lie on the same straight line. The word ‘Collinear’ is a compound word that is made of two words: ‘co’ meaning togetherness and ‘linear’ meaning a line. Collinear points might exist on different planes but not on different lines. Since the points are collinear, it is known as collinearity. Non-collinear points are points which do not lie on a straight line.
Collinear points applications in real life include, students standing in a straight line in an assembly, cars parked on a straight line in the parking lot or a set of balls kept on a straight line. Collinear Points are important in solving real life problems from Euclidean Geometry. Only one straight line can be drawn from a pair of say 3 collinear points. The collinear point formula can be estimated using method of slope, area of triangle or the distance formula.
Read More: NCERT Solutions Class 9 Maths
| Table of Content |
Key Terms: Collinear, Collinearity, Straight Lines, Points, Geometry, Collinear Point Formula, Slope, Area of Triangle, Distance, Non-Collinear
Collinear Points
[Click Here for Sample Questions]
When three or more points lie on the same straight line on a given plane, they are known as Collinear points. These points are aligned in a row or a line. Real-life collinear points include people standing in queue, and bottles kept in a row in the fridge.
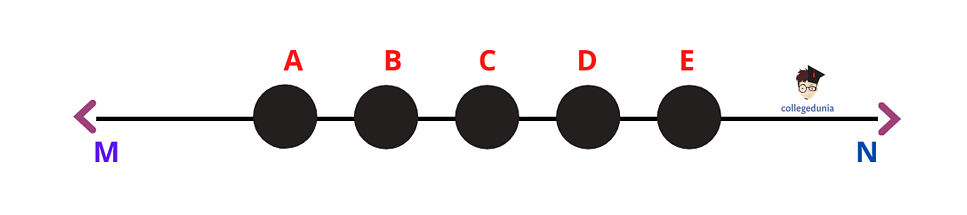
Collinear Points
The video below explains this:
Collinear Point Formulae Detailed Video Explanation:
Also Read: Intersecting & Non-Intersecting Lines
Collinear Points in Maths
[Click Here for Sample Questions]
In Mathematics, Collinear Points are points that are positioned on the same straight line. In the figure below, points (A, B, C,D, E) and points (I, H, C, F, G) are collinear.
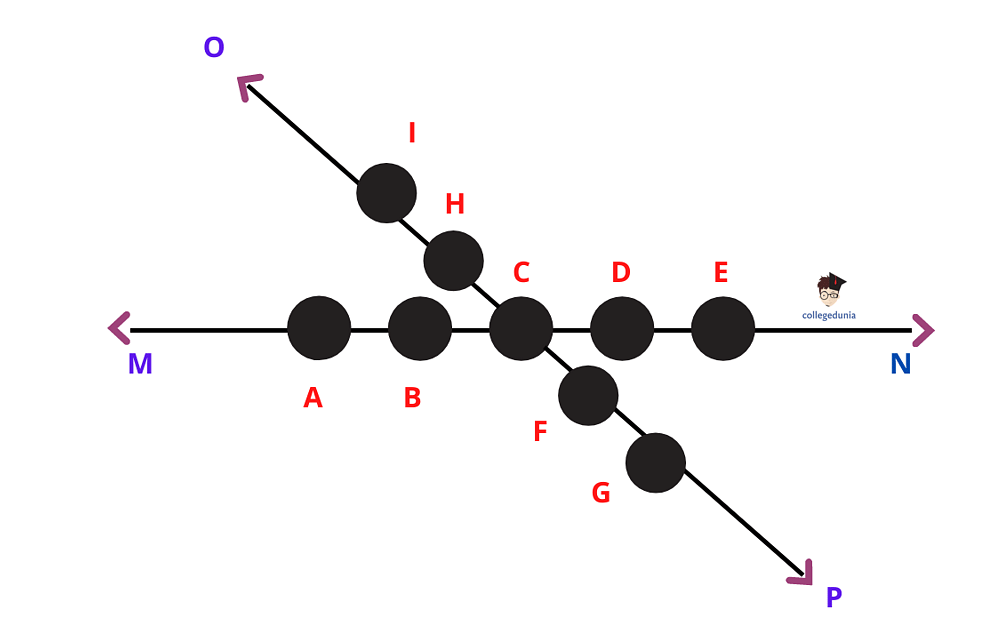
Collinear Points in Maths
Do Check Out:
| Important Concepts Related to Collinear Points | ||
|---|---|---|
| Distance between Two Points | Horizontal and Vertical Lines | Lines and Angles |
| Vertex | Transversal | Properties of Parallel Lines |
| Angle Formula | Obtuse Angle | Linear Pair of Angles |
Formulas of Collinear Points
[Click Here for Sample Questions]
There are three basic ways of finding if three points are collinear or not.
Slope Formula Method
If the slope of any two pairs of points is the same, then the three points are definitely on the same line and they are collinear.
For example, Imagine there are three points- A, B, and C. So the pairs are AB, BC, and AC.
So, if Slope of AB= Slope of BC, then A, B, and C are collinear points.
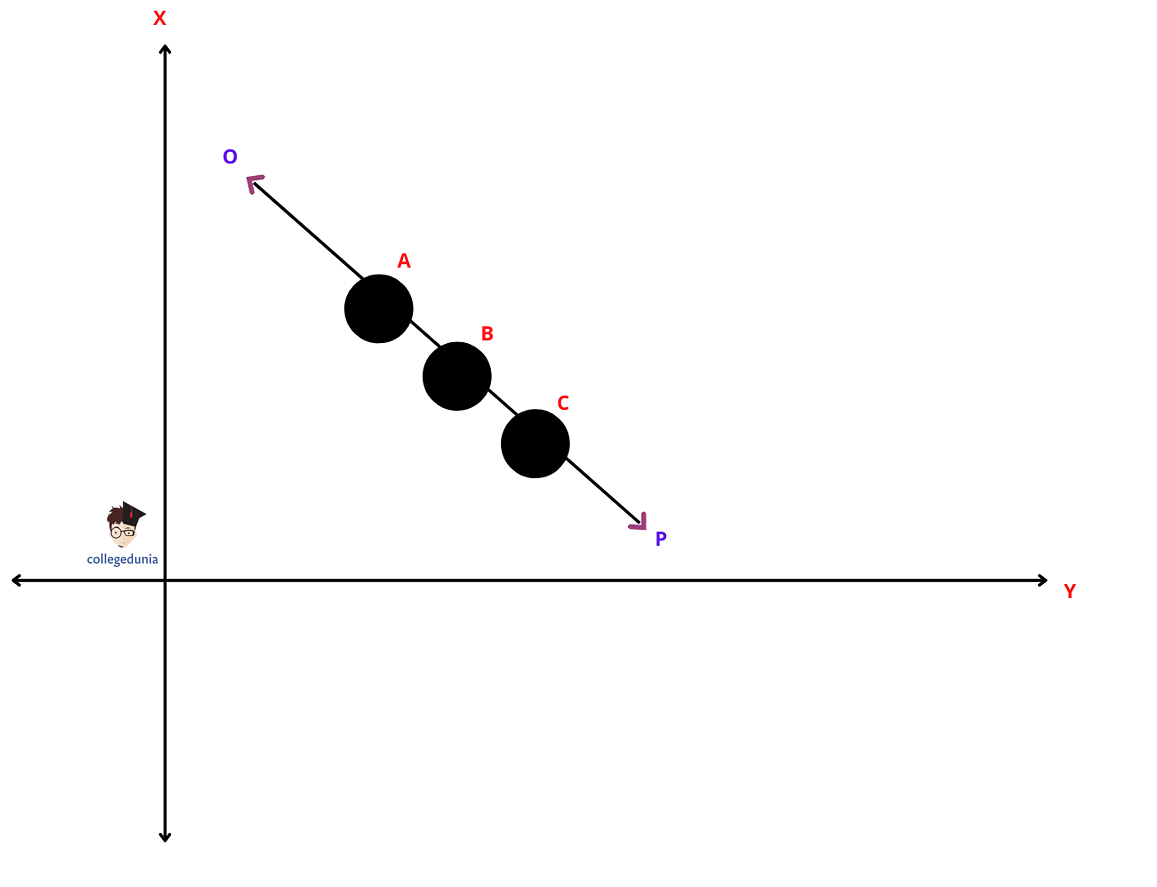
Slope Formula Method
Also Read: Three Dimensional Geometry
Area of the Triangle Method
Another method to prove whether the points are collinear points or not is by finding the area of the triangle formed by the three points. If the area is 0, the points are collinear.
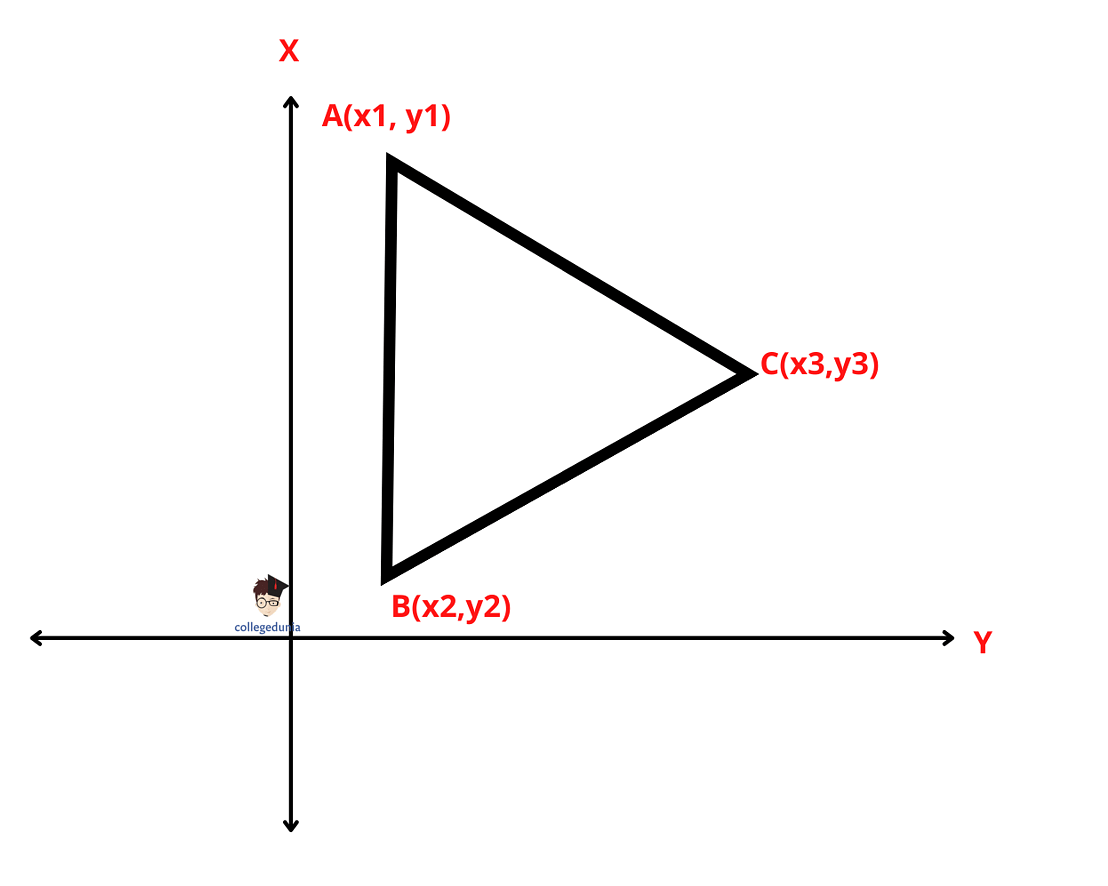
Area of the Triangle Method
For Example, The three points A(x1, y1), B(x2, y2), and C(x3, y3) are collinear, then by remembering the formula of area of the triangle formed by three points we get;
(1/2) | [x1(y2 – y3) + x2(y3 – y1) + x3[y1 – y2]| = 0
Also Read: Lines and Angles MCQs
Distance Method
If the distance between the 1st point and 2nd point added to the distance between 2nd point and 3rd point is equal to the distance between 1st and 3rd point, then all the three points are collinear.
For example, If we take A, B, and C as any three collinear points, then,
Distance from A to B + Distance from B to C = Distance from A to C
So, A, B and C are collinear points
Now, by the distance formula we know, the distance between two points (x1, y1) and (x2, y2) is given by;
D=√(x2−x1)2+(y2−y1)2
Non-Collinear Points
[Click Here for Sample Questions]
Points that are not on the same line and through which a straight line can never be formed, are known as non-collinear points.
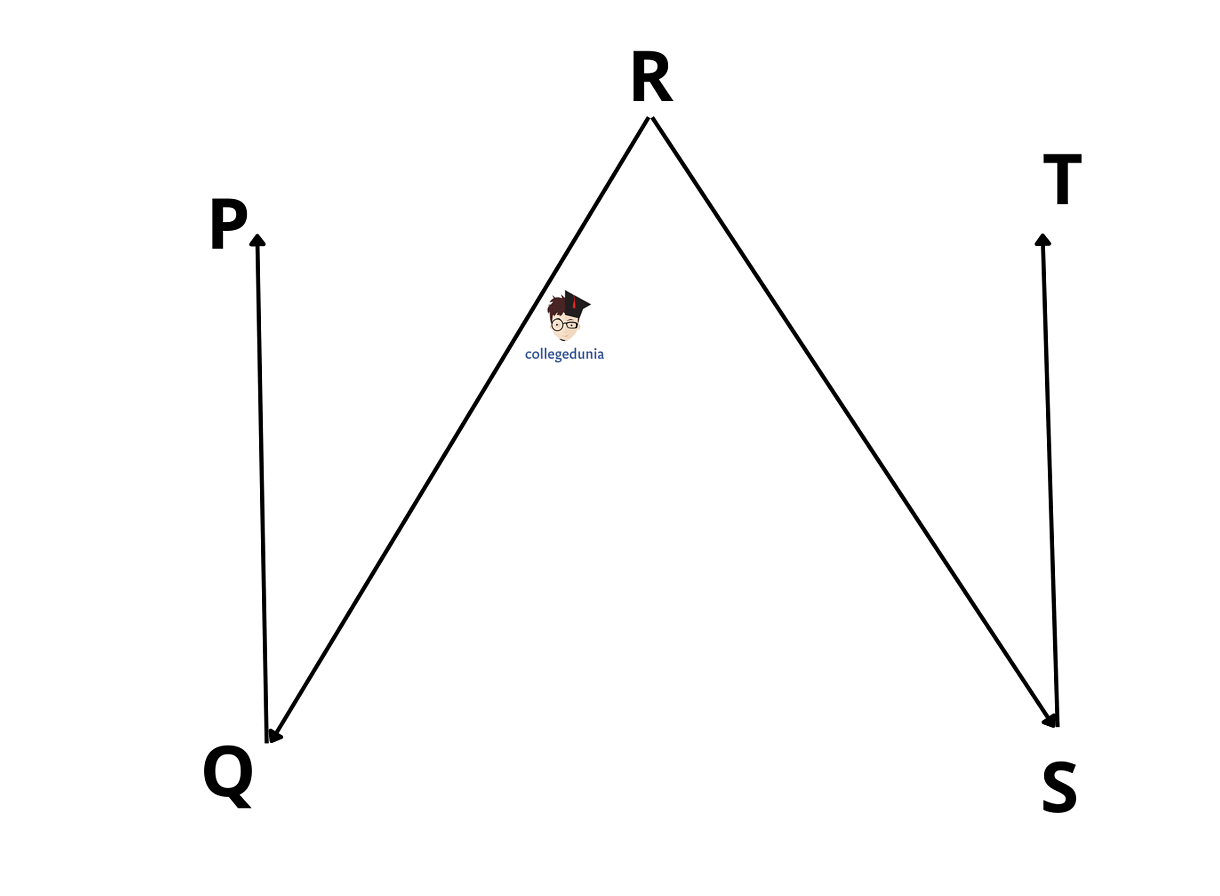
For Example, Let consider the following figure, we cannot draw lines combining the points P, Q, R, S & T. Thus, they are non-collinear points.
Also Read: Corresponding Angles Axiom
Solved ExamplesQues: Prove that points A(5, -2), B(4, -1) and C(1, 2) are collinear points using the Distance Method. Solution : Distance between any two points (x1, y1) and (x2, y2) is d = √[(x2 - x1)2 + (y2 - y1)2] To find the lengths AB, BC and AC using the formula, AB = √[(4 - 5)2 + (-1 + 2)2] AB = √[(-1)2 + (1)2] AB = √[1 + 1] AB = √2 BC = √[(1 - 4)2 + (2 + 1)2] BC = √[(-3)2 + (3)2] BC = √[9 + 9] BC = √18 BC = 3√2 AC = √[(1 - 5)2 + (2 + 2)2] AC = √[(-4)2 + (4)2] AC = √[16 + 16] AC = √32 AC = 4√2 Therefore, AB + BC = √2 + 3√2 = 4√2 = AC Thus, AB + BC = AC This proves that given three points A, B, and C are collinear. Ques: Prove that the given three points (4, 4), (-2, 6), and (1, 5) are collinear points using Slope Formula Method. Solution: Formula: m = (y2 - y1)/(x2-x1) Step 1 : AB’s Slope : (x1, y1) ==> (4 , 4) and (x2, y2) ==> (-2 , 6) m = (6 - 4) / (-2 - 4) = 2/(-6) = -1/3 Step 2 : BC’s Slope : (x1, y1) ==> (-2, 6) and (x2, y2) ==> (1, 5) m = (5 - 6) / (1 - (-2)) = (-1 )/(1 + 2) = -1/3 Step 3 : Slope of ‘AB’ = Slope of ‘BC’ Hence, the given points are collinear |
Things to Remember
- Three or more points lying on the same straight line are known as the collinear points.
- Points that are positioned at non-linear positions on which a straight line cannot be formed are known as non-linear points.
- There are three main ways of finding whether points are collinear or not.
- If three points are collinear, the slopes formed from any two points are the same as the slope formed by the other two.
- The area of the triangle formed by any three collinear points will always be zero.
Also Read:
Sample Questions
Ques. What are collinear points in Geometry? (1 Marks)
Ans: In Geometry, if three or more points are aligned on a straight line, then those points are collinear.
Ques. What is the meaning of the words ‘collinear’? (2 Marks)
Ans: The word collinear is a compound word that is composed of two Latin terms; ‘co’ meaning togetherness and ‘linear’ meaning line. So, collinear means together in a line.
Ques. Give some examples of non-collinear points? (2 Marks)
Ans: Few real-life examples of non-linear points are-
- Players scattered in the field during the match
- Scattered pieces in a carrom board
Ques. What is the formula of collinearity? (2 Marks)
Ans: The formula of collinearity is-
Three collinear points are A, B, and C, then, AB + BC = AC.. If the area is equal to zero, then the points will be collinear. For example, if three points A (a1, b1), B (a2, b2) and C (a3, b3) are collinear, then [a1(b2 - b3) + a2( b3 - b1)+ a3(b1 - b2)] = 0.
Ques. What is the difference between collinearity and coplanarity? (3 Marks)
Ans: Collinearity is the property of the three or more points which lie on the same straight line, whereas, Coplanarity is the property of the points which are positioned on the same plane.
Ques. Can collinear points be coplanar as well? (3 Marks)
Ans: Yes, we can consider collinear points to be coplanar as well. If the points are collinear then most necessarily positioned on any of the infinite numbers of planes. Hence, collinear points are coplanar, but coplanar points might or might not be collinear.
Ques. What are the three basic ways of proving collinear points? (3 Marks)
Ans: There are three ways of proving Collinear points-
- Area of the triangle method
- Distance method
- Slope formula method
Ques. What are some real-life examples of collinear points? (3 Marks)
Ans: Some of the real-life examples of collinear points are-
- Numbers on a ruler
- Commuters seated on a train
- Plants in one row in a garden
- Bottles in a row in the fridge
- Students of a class standing in a line during a school assembly
Do Check Out:






Comments