
Content Strategy Manager
A perpendicular line intersects another line and equalises the angles between them. Remember that there are no measurements in pure geometry, such as degrees. As a result, while it's easy to conceive of a perpendicular line as one that forms two 90-degree angles, we should resist and refer to them as two right angles instead. There are several methods for creating a line that is perpendicular to another. In general, we can create a line that intersects another line at a right angle. This line can alternatively be constructed to pass through a given location rather than along the given line. We can also build a perpendicular line to intersect the line at a specific place.
| Table of Content |
Key Terms: Perpendicular, Lines, Perpendicular Bisector, Arc, Right Angle, Angles
What are Perpendicular Lines?
[Click Here for Sample Questions]
Perpendicular lines can be defined as any two lines that intersect each other in such a way that the angle formed between them is a right angle. To determine whether two lines intersecting each other at a certain point are perpendicular or not, we multiply the slopes of the lines. If the answer is equal to -1, then the lines are said to be perpendicular. The key difference between parallel and perpendicular lines is that parallel lines never intersect each other whereas perpendicular lines intersect each other at right angles.
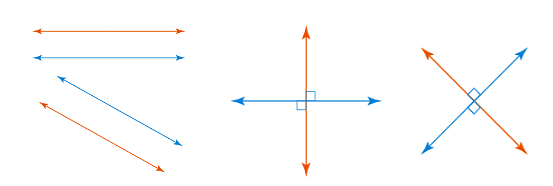
Parallel Lines and Perpendicular lines
Constructing a Perpendicular From a Point Given on the Line
[Click Here for Sample Questions]
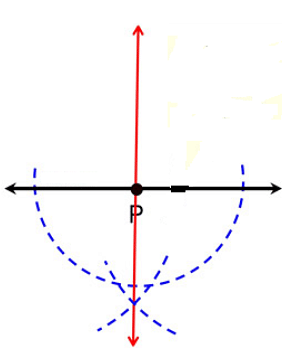
Consider the line shown below .

Perpendicular line
Given: Point P on a given line
Steps to construct a line through P perpendicular to a given line:
- Swing an arc of any size below the line that crosses the line twice with your compass point on P. You'll create a semicircle. (Note: While drawing this arc above or below the line, drawing it below the line prevents the construction lines from intersecting.)
- Extend the compass even more.

Arc
- Make a little arc above the line with the compass point where the arc crossed the line on one side (the arc could be below the line if you prefer).
- Place the compass point where the previous arc crossed the line on the other side and construct another arc without adjusting the span on the compass. Your two little arcs should cross each other.
Arc crossed
- Connect the junction of the two tiny arcs to point P with a straightedge.
Proof of Construction
This construction is essentially a ‘Bisect An Angle’ construction variation. The straight angle P was cut in half by this construction. This structure produced two 90o angles because a straight angle contained 180o. A perpendicular was generated because two right angles were formed.
Also Read:
| Topics Related to Chapter | ||
|---|---|---|
| Lines and Angles | Pairs of Angles | Modern Periodic Table |
| Organic Chemistry | Redox Reactions | Equilibrium |
Constructing a Perpendicular From a Point Away From the Line
[Click Here for Sample Questions]
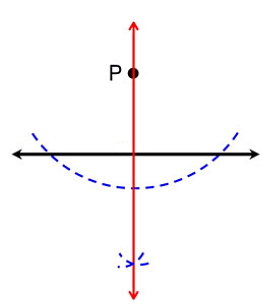
Consider the line shown below.

Given: Point P away from the given line.
Steps to construct a line through P perpendicular to the given line:
- Set your compass to P and swing an arc of any size across the line twice.
- Make a little arc below the line with the compass point on one of the two points where the arc crossed the line (on the side where P is not located).
- Place the compass point on the other side of the line where the first arc crossed the line and make another small arc below the line without changing the span on the compass. The two small arcs should cross each other (on the side of the line opposite of point P).
- Connect the junction of the two tiny arcs to point P with a straightedge.
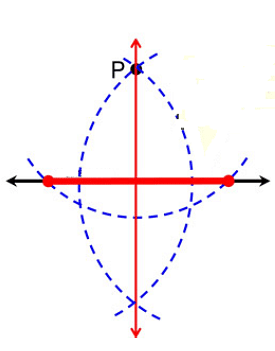
Proof of Construction
Mentioned below is the proof of construction:
- The points of intersection with the first arc are A and B, the intersection of the two smaller arcs is C, and the intersection of the perpendicular with the supplied line is D.
- Because they were built as radii of the same circle, PA = PB and AC = BC.
- These parts are also in line with one another. PBC is congruent to PAC by SSS when using pcas as a common side.
- APC and BPC are congruent according to CPCTC. SAS now considers APD to be consistent with BPD, with a common side PD.
- PDA and PDB are consistent according to CPCTC.
- These two angles are supplementary because they form a linear pair.
- Right angles are formed when two angles are both congruent and supplementary.
Things to Remember
[Click Here for Sample Questions]
- Perpendicular lines are formed when two lines connect at right angles to form right angles. Perpendicular lines are coplanar and intersect at right angles since they are in the same plane.
- The word intersect refers to a point where two lines overlap or meet. A perpendicular is a line that intersects another at a 90° angle.
- Arcs can be used to cut a line segment in half.
- A ruler may be used to draw straight lines, a protractor can be used to measure and draw angles, and a compass can be used to draw arcs that are a particular distance from a point.
- We frequently need to bisect lines or angles when constructing or drawing geometric figures.
- To bisect anything implies to divide it into two equal sections. There are several methods for bisecting a line segment.
Also Read:
| Topics Related to Chapter | ||
|---|---|---|
| Types Of Energy | The Principle of Conservation of Energy | Modern Periodic Table |
| Organic Chemistry | Redox Reactions | Equilibrium |
Sample Questions
Ques. The two lines that connect at right angles inside the kite are perpendicular. Make a list of how many right angles are formed at the intersection. (2 marks)

Ans. A kite is a symmetrical shape. As a result, it has two equal and opposite angles. Its diagonals aren't all the same length, but the larger one divides the shorter one in half at right angles. There are four right angles at the intersection point because the two diagonals of the kite AD and BC connect at right angles or 90 degrees.
Ques. Make a line AB and place a point P on the outside of it. Draw a line CD that runs parallel to AB and passes through point P. (3 marks)
Ans. Construction steps are as follows:

- Draw an AB line.
- Join PQ with a point Q on AB and a point P outside AB.
- Draw on the arc to cut AB at X and PQ at Z with Q as the centre and any radius.
- Draw an arc cutting QP at Y with P as the centre and the same radius.
- Draw an arc to cut the preceding arc at E, with Y as the centre and the radius equal to XZ.
- To get the desired line, join PE and produce it on both sides.
Ques. What is a perpendicular bisector? (2 marks)
Ans. A perpendicular bisector is a line segment that meets another line segment perpendicularly and divides it into two equal-sized halves. A rule, a compass, and a pencil can be used to draw a perpendicular bisector. When two lines intersect at 90 degrees or at right angles, they are perpendicular to each other. On the other hand, a bisector is a line that splits a line into two halves. A perpendicular bisector of a line segment XY intersects it at 90 degrees and divides it into two halves.
Ques. What characteristics does a perpendicular bisector have? (4 marks)
Ans. Properties of a perpendicular bisector are:
- Creates two congruent segments from a line segment or a line.
- Divides a triangle's sides into congruent sections.
- They form a 90-degree angle with the line being bisected.
- They cross the line segment exactly in the middle.
- The circumcenter of a triangle is the place where the perpendicular bisectors intersect.
- They meet inside an acute triangle, outside the triangle in an obtuse triangle, and at the hypotenuse in right triangles.
- The perpendicular bisector's points are equidistant from both ends of the bisected segment.
- For a given line segment, there can only be one.
Ques. How to construct a perpendicular bisector? (2 marks)
Ans. A ruler and a compass can be used to make a perpendicular bisector on a line segment. The built perpendicular bisector separates a line segment into two equal pieces halfway, resulting in two congruent line segments.
Ques. What is a triangle's perpendicular bisector? (2 marks)
Ans. A perpendicular bisector of a triangle is a line segment that bisects its sides while remaining perpendicular to them. They do not have to travel through the triangle's vertices, but they must pass through the midway of the sides. The perpendicular bisector of the triangle's sides is perpendicular to the middle of the triangle's sides.
Ques. How can you tell if two lines are perpendicular? Are rhombus' diagonals perpendicular to each other? Is it possible to say the same thing about a rectangle? (2 marks)
Ans. When two lines connect at a 90° angle, they are perpendicular. Because the diagonals of a rhombus intersect at a 90° angle, we can say that the diagonals of a rhombus are perpendicular to one another. Because the diagonals of a rectangle do not intersect at a 90° angle, we can say that the diagonals of a rectangle are not perpendicular to one another.
Ques. Construct the perpendicular bisector of a line segment 10 cm. (3 marks)
Ans. To create the perpendicular bisector of a line segment AB = 10 cm. Construction steps are as follows:
- Construct two arcs on both sides of the line segment AB and label them P and M, using A and B as centres and a radius greater than (1/2)AB.
- Join P and M.
- Allow line PM to cut the AB portion of the line at Q.
- The requisite perpendicular bisector AB is then line PMQ.
Ques. Differentiate between parallel and perpendicular lines. (3 marks)
Ans. Lines that do not intersect and are always the same distance apart are called parallel lines. The symbol || is used to represent two parallel lines. Here are a few examples:
- The straight ladder's steps
- A rectangle's two opposite sides
Perpendicular lines are those that make a straight angle when they intersect. The symbol ⊥ is used to represent two perpendicular lines. Here are a few examples:
- The corner of two walls
- The letter "L"
Ques. Which of the following shapes has perpendicular sides and why? (5 marks)
(1) Square
(2) Trapezium
(3) Rectangle
(4) Rhombus
(5) Right triangle
(6) Equilateral triangle
Ans. 1. Four lines make up the square. A square has four right angles since each line is perpendicular to two other lines. The line AB is parallel to the line BC. BC, like CD, AB, and so on, is perpendicular to each other. To clarify, a square has right angles, and a square formed by drawing two more lines in the corner of a right angle is also used to represent a right angle.
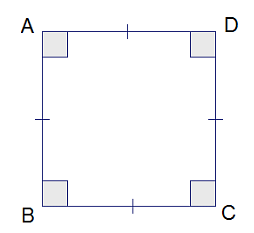
- A trapezium is a quadrangle in which one pair of opposite sides is parallel to one other while the other pair is not. The bottom of a trapezium is normally drawn using one of the parallel edges. The bases are the parallel edges, and the sides are the non-parallel edges. So, there are no perpendicular lines. Special trapeziums come in a variety of shapes and sizes. One side of a "right trapezium" is perpendicular to the bases, resulting in two right angles. So, the lines are perpendicular.

- Right angles can also be found in rectangles. A rectangle, like a square, has four right angles. This means it has lines that are perpendicular to each other.

- Rhombus has equal lines but no perpendicular lines as clearly shown in the figure. The rhombus has diagonals which bisect each other at right angles, so the diagonals are perpendicular to each other, whereas the sides are not.

- A right triangle has perpendicular lines as shown in the figure.

- An equilateral triangle has all angles equal to 600, so it does not have perpendicular lines.

Read More:
Read More:
| Mathematics Study Guide | ||
|---|---|---|
| Trigonometry | Mensuration | Math Study Material |
| Arithmetic | Geometry | Number Systems |
| Math Formula | Difference between in maths | Algebra |






Comments