Muskan Shafi Education Content Expert
Education Content Expert
Triangle Theorems are propositions or statements in Geometry that deal with the various types and properties of a triangle. They have significant use in geometry and are used to prove the properties or the similarity of triangles.
- Triangle is a two-dimensional and three-sided polygon that has three edges and three vertices.
- The sum of all the angles of a triangle is 180°.
- Scalene Triangle, Isosceles Triangle, and Equilateral Triangle are the three types of triangles based on their sides.
- On the basis of angles, the types of triangles are Right-angled Triangle, Acute-angled Triangle, and Obtuse-angled Triangle.
- Area of a triangle is given as A = ½ x Base x Height.
Read More: NCERT Solutions for Class 7 Mathematics The Triangle and its Properties
Key Terms: Triangle, Triangle Theorems, Pythagoras Theorem, Basic Proportionality Theorem, Isosceles Triangle, Equilateral Triangle
Triangle Definition
[Click Here for Sample Questions]
Triangle is the simplest polygon in geometry that has three sides, three vertices, and three edges.
- It is a closed two-dimensional shape made of three straight lines.
- The point where the two straight lines intersect each other is called the Vertex.
- There are three vertices in a triangle and each vertex forms an angle.
- The sum of the three internal angles of a triangle is 180 degrees.

Triangle
Read More:
Properties of Triangle
[Click Here for Sample Questions]
The properties of triangle are as follows:
- A triangle has three sides, three vertices, and three edges.
- The sum of the internal angle of a triangle is equal to 180°.
- The sum of the exterior angles of a triangle is 360°.
- The sum of consecutive interior and exterior angles of a triangle is supplementary.
- The sum of the two sides of the triangle is more than the length of the third side.
- The difference between the lengths of any two sides of a triangle is less than the third side.
- The shortest side of the triangle is always opposite the smallest interior angle.
- The longest side of the triangle is always opposite the largest interior angle.
Types of Triangles
[Click Here for Sample Questions]
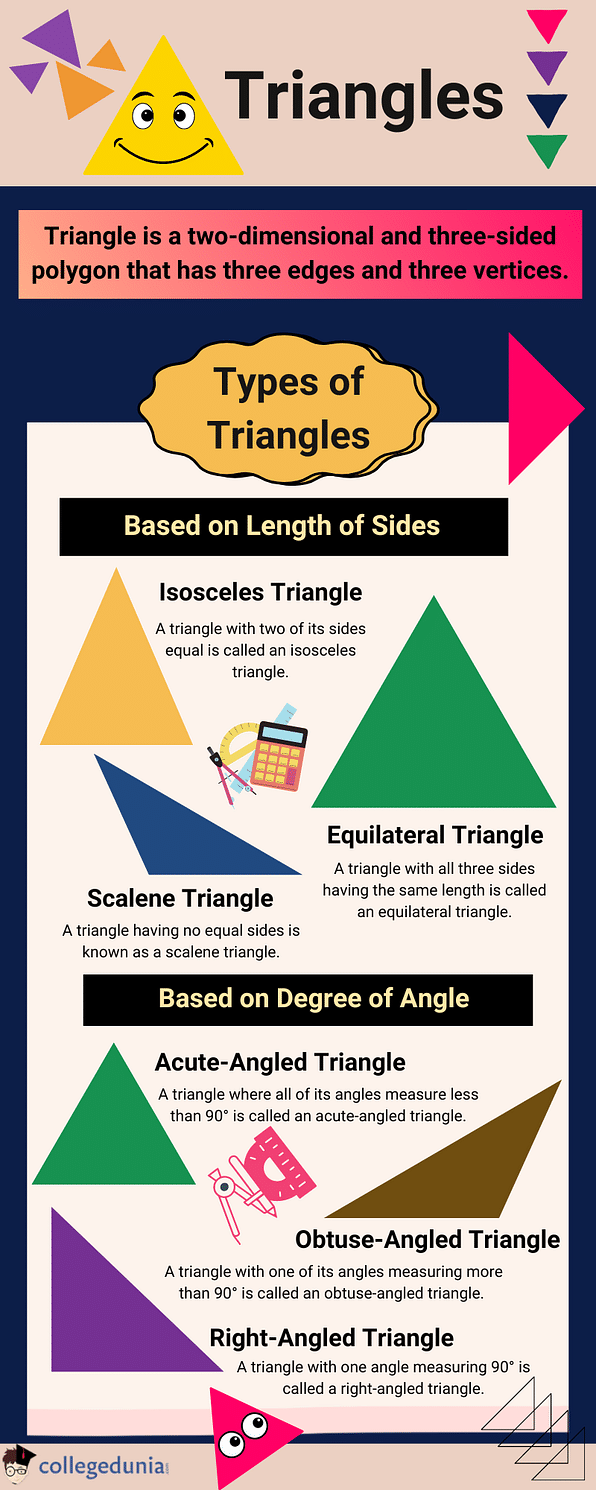
Triangles can be classified into various types based on the length of their sides and the degree of the angle. The different types of triangles are as follows:
Based on Length of Sides
On the basis of the length of the sides, there are three types of triangles:
- Equilateral Triangle: A triangle with all three sides having the same length is called an equilateral triangle.
- Isosceles Triangle: A triangle with two of its sides equal is called an isosceles triangle.
- Scalene Triangle: A triangle having no equal sides is known as a scalene triangle.

Based on Angles
On the basis of the measurement of the angles, there are three types of triangles which are as follows:
- Obtuse-Angled Triangle: A triangle with one of its angles measuring more than 90° is called an obtuse-angled triangle.
- Right-Angled Triangle: A triangle with angles measuring 90° is called a right-angled triangle.
- Acute-Angled Triangle: A triangle where all of its angles measure less than 90° is called an acute-angled triangle.
Triangles
Triangle Theorems
[Click Here for Sample Questions]
Triangle Theorems are used to prove various properties and related problems in Geometry. The important triangle theorems are listed as follows:
Triangle Inequality Theorem
According to Triangle Inequality Theorem, one of the sides of the triangle is shorter than the other two sides. This theorem is an essential criterion to form a triangle. A triangle cannot be created without satisfying this theorem.
Let us assume a Triangle ABC with sides AB, BC, and CA.

According to Triangle Inequality Theorem,
| AB + BC > CA |
Read More: Triangles Important Questions
Triangle Sum Theorem
According to the Triangle Sum Theorem, the sum of the internal angles of a triangle is equal to 180o.
Assume a triangle ABC, then, according to the theorem,
| ∠A + ∠B + ∠C = 180° |
Basic Proportionality Theorem
Basic Proportionality Theorem states that when a line is drawn parallel to one side of a triangle to intersect the midpoints of the other two sides, then the two sides are divided in the same ratio.
Assume that ABC is a triangle and DE is a line parallel to BC such that it intersects AB at D and AC at E.

Thus, according to Basic Proportionality Theorem,
| \({AD \over DB} = {AE \over EC}\) |
Pythagoras Theorem
In a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the square of the base and the square of the perpendicular. The longest side of the triangle is termed the hypotenuse, and the other two sides are perpendicular and base, respectively.
Assuming a Triangle ABC, with hypotenuse AB, base BC, and perpendicular CA, then the Pythagoras theorem states that,
| (AB)2 = (BC)2 + (CA)2 |

Pythagoras Theorem
Exterior Angle Theorem
The exterior angle of a triangle is equal to the sum of the corresponding interior angles.
In the given triangle, according to the given theorem, ∠3 = ∠1 + ∠2

Read More: Exterior Angle Theorem
Triangle Similarity Theorems
[Click Here for Sample Questions]
Triangle Similarity Theorems aim at proving the similarity between any two given triangles. Under these theorems, various conditions are stated according to which two or more triangles can be proved similar. Similar triangles are depicted using the congruence sign as ΔABC~ ΔQPR.
The three main triangle similarity theorems are:
SSS Similarity Theorem
- It is the Side-Side-Side similarity theorem.
- When all three sides of two triangles have the same length or are in the same proportion, they are said to be congruent.
- For the sides to be congruent, all three sides need to be proportionate.
AA Similarity Theorem
- It is the Angle-Angle similarity theorem.
- When two or three angles of the triangle are of the same measure, they are congruent.
- Even when only two of the angles are the same, by the Triangle Sum Property, the third angle is itself the same.
SAS Similarity Theorem
- It is the Side-Angle-Side similarity theorem.
- When two sides are proportional in a triangle, and the angle between the two sides is equal, then the triangles are congruent.
Check More:
Things to Remember
- Triangle is a closed polygon with three sides, three angles, and three vertices.
- Equilateral triangle, Isosceles triangle, and Scalene triangle are the three main types of triangles.
- Triangle Theorems are integral in geometry to prove the properties and congruency of triangles.
- The angle sum property of the triangle states that A°+ B°+ C° = 180°.
- According to the Pythagoras Theorem, (AB)2 = (BC)2 + (CA)2.
- Triangle similarity theorems are used to prove the similarity between two triangles.
Sample Questions
Ques. In the right ΔABC, the lengths of two of the sides, i.e. the base and perpendicular, are given as 9 cm and 10 cm respectively. What is the length of the hypotenuse? (3 Marks)
Ans. Given that
- Base = 9 cm
- Perpendicular = 10 cm
According to the Pythagoras theorem,
(AB)2 = (BC)2 + (CA)2
c2 = a2 + b2
c2 = 81 + 100
c2 = 81 + 100 = 181
c = 13.4 cm
Thus, the length of the hypotenuse is 13.4 cm.
Ques. A ladder of length 20 cm is placed against a wall so that the ladder's footing has a distance of 10 cm from the wall. What is the wall height at which the ladder has reached the wall? (3 Marks)
Ans. The ladder, floor, and wall are forming a triangle, which is assumed to be ΔABC. Let the length of the ladder, 20 cm be equal to AB, the base 10 cm be equal to CA, and the wall height is CB.
Since the angle between the floor and the wall is 90°, ΔABC is a right-angled triangle.
Using the Pythagoras Theorem,
AB2= CA2 + CB2
400 = 100 + CB2
300 = CB2
√300 = CB2
CB = 17.3 cm
Thus, the height of the wall is 17.3 cm.
Ques. State any three important properties of triangles. (3 Marks)
Ans. The three important properties of triangles are as follows:
- The sum of the angles of the triangle is equal to 180 degrees.
- The exterior angles of a triangle give a sum of 360 degrees.
- The shortest side of a triangle is always opposite the smallest angle of a triangle.
Ques. In a right ΔABC, the base and perpendicular are 5 cm and 3 cm respectively. What will be the hypotenuse? (3 Marks)
Ans. According to the question,
- Base = 5 cm
- Perpendicular = 3 cm
According to the Pythagoras theorem, we have
(AB)2 = (BC)2 + (CA)2
Let c be the hypotenuse, and a and b be the other two legs of the right-angled triangle.
c2 = a2 + b2
c2 = 25 + 9
c2 = 25 + 9= 34
c = 5.8 cm
Thus, the hypotenuse of the triangle is 5.8 cm.
Ques. How to prove two triangles are similar? (3 Marks)
Ans. In order to prove the similarity or congruency of two triangles, the triangles should satisfy any of the three given similarity theorems:
- AA (Angle-Angle) Similarity Theorem: If two angles of the given two triangles are similar, then they are similar.
- SSS (Side-Side-Side) Similarity Theorem: When three sides of two triangles are the same or in the same ratio, then they are congruent.
- SAS (Side-Angle-Side) Similarity Theorem: When two sides of two triangles are proportional to each other, and the angle between them is similar or the same, then the triangles are congruent.
Ques. The sides of the triangle are in the ratio 4:6:7. Determine whether it is a right-angled triangle or not. (3 Marks)
Ans. Let the triangle be ΔQPR, and the sides in the ratio 4:6:7 be equal to 4x, 6x, and 7x.
So,
- QP = 4x
- PR = 6x
- RQ = 7x
For the triangle to be right-angled,
RQ2 = QP2 + PR2
49x = 16x + 36x
Since the sum, according to the equation, is not equal. Therefore, ΔQPR is not a right-angled triangle.
Ques. The lengths of two sides of a right-angled triangle are 10 cm and 11 cm. Determine the hypotenuse. (3 Marks)
Ans. The two sides are given as 10 cm and 11 cm.
Using Pythagoras Theorem,
(a)2 = (b)2 + (c)2
Substituting the values, we get
c2 = 100 + 121
c2 = 100 + 121 =221
c = 14.8 cm
Thus, the hypotenuse of the triangle is 14.8 cm.
Ques. What are the types of a triangle? (2 Marks)
Ans. There are six major types of triangles:
- Scalene Triangle
- Isosceles Triangle
- Equilateral Triangle
- Acute Triangle
- Obtuse Triangle
- Right Triangle
Ques. The two sides of a triangle are 10 cm and 12cm. Between what two measures should the size of the third side be? (3 Marks)
Ans. Referring to the properties of the triangle, the third side of the triangle is smaller than the sum of the other two sides. Therefore, let the unknown side be C.
So, 10 + 12 > C
22 > C ……… (1)
Also, 10 + C > 12
C > 2 ……… (2)
Therefore, according to equations one and equation two,
2 < C < 22,
It means that the length of C is greater than 2 and less than 22.
Ques. The base and hypotenuse of a right ΔABC are given as a = 7 cm, and b = 2 cm. Find the hypotenuse. (3 Marks)
Ans. It is given that,
- Base = 7 cm
- Perpendicular = 2 cm
Using Pythagoras Theorem,
(AB)2 = (BC)2 + (CA)2
c2 = a2 + b2
c2 = 49 + 4
c2 = 49 + 4 = 53
c = 7.2 cm
Therefore, the length of the hypotenuse is 7.2 cm.
Check-Out:






Comments