
Collegedunia Team Content Curator
Content Curator
Area of triangle is the amount of space enclosed within the boundaries of the triangle. The area of a triangle is determined by calculating half the product of the length of the base and height of the triangle. Area of a Triangle can be measured in square units with the standard unit being square meters (m2). The area of triangle is determined by the formula.
A = ½ b x h
Depending on the types of triangles, the formula for the area also changes accordingly.
| Table of Content |
Key Terms: Triangles, Area of Triangle, Length, Height, Base, Area of Right Angled Triangle, Area of Equilateral Triangle, Area of Scalene Triangle
What is the Area of a Triangle?
[Click Here for Sample Questions]
Area of triangle is the total region enclosed by the three sides of any given triangle. To find the area of a tri-sided polygon, we have to know its base (b) and height (h). It is applicable to all the types of triangles – scalene, isosceles or equilateral. The base and height of the triangle are perpendicular to each other in Area of a Trinagle. The area of a triangle is measured in m2 or cm2.
| Area of a Triangle = ½ x base x height |
As long as the value of base and height is available, we can find the area of any type of triangle using the above mentioned formula. To understand better go through the following example.
| Example: Find the area of an isosceles triangle with base b = 5 cm and height h = 12 cm. Solution: Using the formula of area of triangle, A = 1/2 × b × h = 1/2 × 5 cm × 12 cm = 5 cm × 6 cm = 30 cm2 Area of Triangle = 30 cm2 |
Apart from the formula given above, Heron’s formula can also be used to calculate the area of a triangle when the length of its three sides is known. Trigonometric functions can also be used to determine the triangle’s area when its two sides and the angle formed between them are known.
Discover about the Chapter video:
Determinants Detailed Video Explanation:
Also Read: Height and Difference
Area of a Right Angled Triangle
[Click Here for Sample Questions]
Right-angled triangle has one of its angles, 90 degrees. It can either be Isosceles or scalene but never an equilateral. The opposite side to the right angle is called a hypotenuse. Pythagoras theorem is only applicable to Right angled triangle.
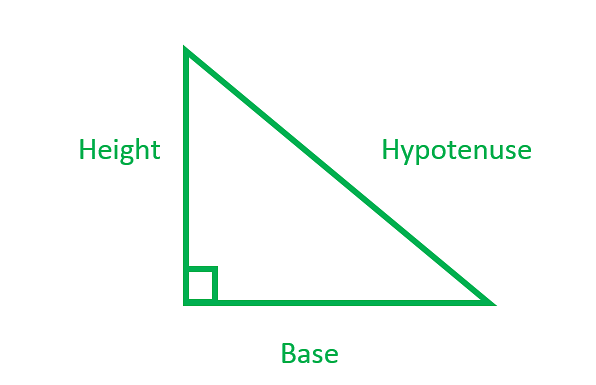
Right Angled Triangle
The area of a right-angled triangle is given by the formula,
| A = ½ (b x h) |
Where,
b → Base of the triangle
h → Height of the triangle
| Example: Find the area of a right angle triangle with base b = 4 cm and hypotenuse H = 10 cm. Solution: Using the Pythagoras Theorem height, h = √H2 – b2 = √102 – 42 = √36 = 6 therefore, height h = 6 cm Thus, area of th etriangle = 1/2 × b × h = 1/2 × 4 x 6 = 12 cm2 Area of the triangle = 12 cm2 |
Read More: Right Angled Triangle Theorem
Area of an Equilateral Triangle
[Click Here for Sample Questions]
Equilateral triangle has all of its sides equal. The angle between each of the legs of an equilateral triangle is 60 degrees. The Center of an Equilateral Triangle coincides with its centroid. A triangle is equilateral if any two of the circumcenter, incenter, centroid or orthocenter coincide.

Equilateral Triangle
The area of the Equilateral triangle is given by,
| A = √3/4 x a2 |
Where,
a → Length of the side of the Equilateral triangle
The altitude or height of an Equilateral triangle can be found by using the formula,
| h = \(\frac{\sqrt{3}}{2} a\) |
| Example: Find the area of an equilateral triangle whose perimeter is 24 cm. Solution: We know that perimeter of an equilateral triangle is 3a, where a is the side of the triangle. Thus, 3a = 24 cm a = 24/3 cm a= 8 cm Now, area of an equilateral triangle = √3/4 x a2 Area = √3/4 x 82 = 16√3 Area of the triangle is 16√3 cm2 |
Area of Isosceles Triangle
[Click Here for Sample Questions]
In an Isosceles triangle, any two sides and their corresponding angles are equal.
Isosceles Triangle
The area of an Isosceles triangle is given by the formula,
| A = ½ (b x h) |
Where,
b → Base of the triangle
h → Height of the triangle
Since two of the three angles are equal in the Isosceles triangles, if only the value of the unequal angle is given, we can easily find the other two.
Also Read: Isosceles Triangle Theorems
| Example: Find the area of an isosceles triangle with base b = 4 cm and height h = 10 cm. Solution: Using the formula of area of triangle, A = 1/2 × b × h = 1/2 × 4 cm × 10 cm = 2 cm × 10 cm = 20 cm2 Area of Triangle = 20 cm2 |
Check out More PYQ Links:
Area of Scalene Triangle
[Click Here for Sample Questions]
Scalene triangle has all sides with different lengths and angles.

Scalene Triangle
The area of a scalene triangle can be determined by using Heron’s formula which is given by,
| A = √ s (s – a) (s – b) (s – c) |
Where,
s → Semi perimeter (\(\frac{a+b+c}{2}\))
a, b, c → Length of the side of the triangle
If any two sides and one angle of the scalene triangle are known, then the following formula can be used.
- ½ b x c SinA
- ½ c x a SinB
- ½ a x b SinC
| Example: Find the area of a scalene triangle with sides as 10 cm, 12 cm, and 20 cm. Solution: Using Heron’s Formula, semiperimeter s = (10 + 12 + 20)/2 = 21 cm Now, area of the triangle A = √s(s – a)(s – b)(s – c) = √21(21 – 10) (21 – 12)(21 – 20) = √21 x 11 x 9 x 1 = √2079 Area of the triangle is 45. 6 cm2(approximately) |
Check Out:
Units for Area of Triangle
[Click Here for Sample Questions]
The Standard Units for measurement of an area of triangle are Square meter (m2) and square centimetre (cm2). Other Units for the measurement of an area are the following:
- Square millimetres (mm2)
- Square Inches (in2)
- Square kilometres (km2)
- Square Yards. (y2)
Also Check: NCERT Solutions for Class 6 to 12 PDFs
Things to Remember
- Area of triangle is the amount of space enclosed within the boundaries of the triangle.
- The area of an Isosceles triangle and right-angled triangle is given by the formula ½ x base x height.
- The area of an Equilateral triangle is given by the formula A = √3/4 x a2
- The height or altitude of an Equilateral triangle is given by h = \(\frac{\sqrt{3}}{2} a\)
- Heron’s formula for finding the area of a scalene triangle is given by, A = √ s (s – a) (s – b) (s – c).
Also check:
Sample Questions
Ques. The base and height of a right Triangle are 30 meters and 7 m, respectively. Find out the area of the triangle. (2 marks)
Ans. A = ½ (base x height)
= ½ (30m x 7m)
= ½ (210m2)
= 210m2 /2
= 105 m2
Area of a Triangle = 105 m2
Ques. Calculate the area of an Isosceles Triangle whose base is 6 mm and height is 11 mm. (2 marks)
Ans. A = ½ (base x height)
= ½ x 6 x 11
= 33 mm2
Ques. What will be the area of an Isosceles triangle if its side lengths are 7m and 11m? (2 marks)
Ans. Let the base b = 11 m, and a = 7m,
A = ½ [(√a2 – b2 / 4) x b]
= ½ [(√ 72 – 112 / 4) x 11]
= ½ [(√18) x 11]
= 23.1 m2
Ques. Find out the area of an equilateral triangle that has a perimeter of 42mm. (2 marks)
Ans. Perimeter of an equilateral triangle = 3a
3a = 42 mm
a = 42 mm / 3
a = 14 mm
area of an equilateral triangle = (a2 / 4) √3
= (142 / 4) √3
= (14 x 14 / 4) √3
= (196 / 4) √3
= 49 √3 mm2
Ques. Find out the area of a tringle which has three side lengths; 9 mm, 10 mm, 7 mm. (2 marks)
Ans. P = (a + b + c) / 2
P = (9 + 10 + 7)/2
P = 26/2
P = 13
Area = √ {p (p - a) (p - b) (p - c)} [ Because it’s a Scalene Triangle]
= √ {13 (13 – 9) (13 -10) (13 – 7)}
= √ {13 (4) (3) (6)}
= √ {13 x 4 x 3 x 6
= √ 936
= 30.5 mm2
Ques. How can we find the perimeter of a Triangle? (2 marks)
Ans. By using the formula P = a + b + c
Ques. How do you convert centimeters into meters? (2 marks)
Ans. You can change centimetres to meters by dividing it with 100.
For example: 60 cm: 60/100 = 0.6 m.
And you can multiply by 100 to change it into the centimetre.
0.6 m. to cm = 0.6 m. x 100 = 60 cm.
Ques. What’s the difference between area and Perimeter? (2 marks)
Ans. Perimeter is the distance around the outside of a triangle or a rectangle, while the area is the measurement of the space inside a triangle or a rectangle.
Ques. How can we find the ratio of the area of a triangle? (2 marks)
Ans. If the bases of triangles are equal, then the ratio of their area will be equal to the ratio of their heights. And if triangles are similar, then the ratio is the square of the scale factor.
Ques. The base and height of the triangle are in the ratio 3:2. If the area of the triangle is 243 cm² find the base and height of the triangle. (4 Marks)
Ans. Let the common ratio be x.
Then height of triangle = 2x ; base of triangle = 3x
Area of triangle = 243 cm²
= 1/2 × b × h
⇒ 243 = 1/2 × 3x × 2x
⇒ 3x² = 243
⇒ x² = 243/3
⇒ x = √81
⇒ x = √(9 × 9)
⇒ x = 9
Therefore, height of triangle = 2 × 9 = 18 cm
Base of triangle = 3x
= 3 × 9
= 27 cm
Ques. An equilateral triangle board needs to be painted in yellow color. Each side of the signboard measures 8 in. Find the area to be painted yellow. (3 Marks)
Ans. Area of an equilateral triangle is given as:
Area = √3/4 × (Side)2
By substituting value of side-length in the above formula, we get,
= √3/4 × 82
= 16√3
Therefore, Area of a Triangle to be painted yellow = 16√3 inches2.
Ques. If the perimeter of an equilateral triangle is 48 cm. Find its area. (3 Marks)
Ans. Given that perimeter is 48 cm.
We know that in an equilateral triangle, perimeter = 3a
where a = side of the triangle
Thus, 3a = 48 cm
a = 16 cm
Area of an equilateral triangle = (√3a)/4
A = (√3 x 16)/4 cm2
A = 4√3 cm2
Therefore, area of the equilateral triangle is 4√3 cm2.
Also Read:







Comments