
Collegedunia Team Content Curator
Content Curator
Area of an isosceles triangle depends upon the available parameters. An isosceles triangle is a type of triangle which has only two sides to be equal. Angles opposite to these two equal sides are also equal. The usual area for the Isosceles triangle is determined by half of the product of base and height of the Isosceles triangle. The area of Isosceles triangle is given by the formula,
A = ½ base x height
| Table of Content |
Key Takeaways: Isosceles Triangle, Formulas, Base angle theorem, Apex angle
Isosceles Triangle
[Click Here for Sample Questions]
An isosceles triangle is a type of triangle which has only two equal sides/angles. Angles opposite to these equal sides are also equal.
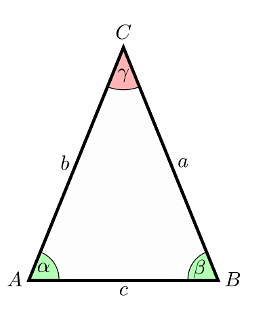
Isosceles Triangle
In the above image, ABC is an isosceles triangle where AB & AC sides are equal in length and the opposite angles ∠ABC & ∠ACB are equal.
Also Read: Similarities of Triangle
Properties of Isosceles Triangle
[Click Here for Sample Questions]
Some of the major properties are listed below:
- Two sides are congruent to each other.
- The third side of an isosceles triangle which is unequal to the other two equal sides is called the base of the triangle.
- The two angles opposite to the equal sides are equal to each other and it is called base angles. And this is a theorem called Isosceles triangle base angle theorem.
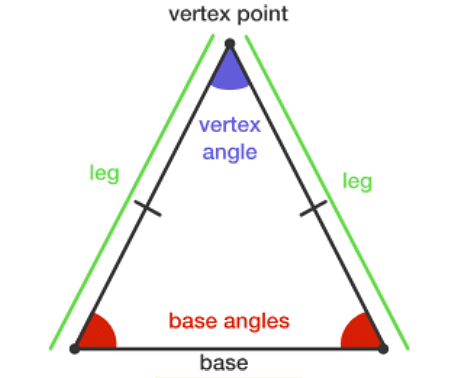
Isosceles Triangle
- The angle which is not congruent to the other angles (base angles) is called the apex angle.
- Upon drawing an altitude from the apex of an isosceles triangle it divides the triangle into two right-angle triangles.
- The perimeter of an isosceles triangle is the sum of all three sides.
Also Read: Section Formula
Area of Isosceles triangle
[Click Here for Sample Questions]
The area of an isosceles angle is the total region covered by all three sides of the triangle in a 2D space.
To calculate the area we can take help from this figure.
Let’s take triangle ADC,
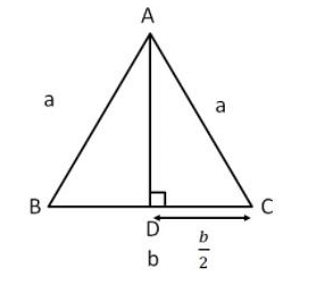
Here,
\(AD^2 = a^2 - \frac{b^2}{4}\)
So, Height AD is given by,
\(AD = \sqrt{a^2 - \frac{b^2}{4}}\)
Now, Area of Isosceles triangle = ½ x base x height\(= \frac{1}{2} \times b \times \sqrt{a^2 - \frac{b^2}{4}}\)
Also Read: Pythagoras Theorem
Calculation of Area
[Click Here for Sample Questions]
The area of an isosceles triangle can be calculated in various ways depending on the known measures of that isosceles triangle. Let’s look at the other formulae that can be used to calculate the area of an isosceles triangle based on different elements –
| Known Parameters of the Isosceles Triangle | Formula to Calculate Area |
|---|---|
| Base & Height | A = ½ × b × h |
| Length of two sides and angle between them | A = ½ × b × a × sin(α) |
| All the sides | A = (\(\frac{1}{2} [\sqrt{a^2 - \frac{b^2}{4}} \times b\)) |
| Two angles and length between them | A = (\(a^2 \times sin (\frac{\beta}{2}) \times sin (\alpha)\)) |
| Isosceles right-angle triangle | A = ½ × a2 |
Things to Remember
[Click Here for Sample Questions]
- An isosceles triangle has two equal sides/angles.
- Angles opposite to the equal sides are congruent to each other.
- Equal angles are called base angle and the other angle is called apex angle.
- The main formula for calculation the area of an isosceles triangle is - ½ * Base * Height.
- The perimeter of an isosceles triangle is the sum of all the three sides.
- The altitude divides an isosceles triangle into two equivalent right-angled triangles.
- Also, the altitude divides the base into two equal parts.
Read More:
Sample Questions
Ques: What is the isosceles right triangle? (2 Marks)
Ans: An isosceles right triangle will have a right angle (90°) and two equal sides. The three angles of an isosceles right triangle will be 90°, 45°, and 45°. The opposite sides of the two 45° angles are congruent.
Ques: Find the area of an isosceles triangle given the length of the base is 20 cm and height is 15 cm? (2 Marks)
Ans: Base of the triangle (b) = 20 cm
Height of the triangle (h) = 15 cm
Area of Isosceles Triangle = (1/2) × b × h
= (1/2) × 20 × 15
= 10 × 15
= 150 cm2
Ques: Calculate the area of the isosceles triangle. (2 Marks)
Ans: At first, we are given two values here one is height = 120 cm and base is 4 m. We must convert the units into the same method.
h = 120 cm = 1.2 m
b = 4 m
Now calculating area, Area = ½ * height * base
= ½ * 1.2 * 4
= 2.4 m²
Ques: Calculate the sides of the isosceles triangle. (3 Marks)
Ans: Calculation sides, h = 1.2 m
b = 2 m (base is divided by 2 as we are taking one isosceles right angle)
By applying Pythagoras theorem, we get,
Side = √(1.2)² + (2)² m
= √1.44 + 4 m
= √5.44 m
= 2.33 m
Ques: Triangle PQR is an isosceles triangle which has an area of 54 cm². The height of the triangle is 12 cm. Determine the length of the base of the triangle. (3 Marks)
Ans: Given, b = 12 cm, Area = 54 cm²
We know, area = ½ * h* b
So, b = (2*area)/h
Now putting the values on the above equation, we get,
b = (2*54)/12
= 108/12
= 9 cm
Ques: Find the length of the base of an isosceles triangle whose area is 243 cm², and the altitude of the triangle is 9 cm. (3 Marks)
Ans: Area of the triangle, A = 243 cm²
Height of the triangle (h) = 9 cm
The base of the triangle = b =?
Area of Isosceles Triangle = (1/2) × b × h
243 = (1/2) × b × 9
243 = (b × 9)/2
b = (243 × 2)/9
b = 54 cm
Ques: Calculate the area of the below isosceles triangle (5 Marks)
Ans: b = 7 m
To find the height of this triangle we need to split the isosceles triangle into two right triangles. Then we can then apply Pythagoras’ Theorem to one of the right triangles to calculate its height.
h² = 7² - 2²
= 49 – 4
= 45
h = √45
= 6.71 (approx.)
Now, Area = ½ * b * h
= ½ * 4 * 6.71 m²
= 13.42 m²
Ques: How to find the area of an isosceles triangle? (3 Marks)
Ans: Follow these steps to find the area of an isosceles triangle –
Step 1 – Determine the value of height and base of the isosceles triangle. If not given then calculate it.
Step 2 – Write down the formula of area = ½ * Base * Height
Step 3 – Put the values into the formula
Step 4 – Calculate the area.
Note: If you are unable to find the height then take the help of the other formulae. You can find the height of the triangle by applying the Pythagoras theorem.
Read More:
| Area of Sector | Areas related to circles | Geometry Formula |
| Circles | Trigonometric Identities | Construction Formula |
| Areas Related to Circles | Perimeter of a Circle | Circumference of a Circle |
Related Links:






Comments