
Content Curator
The formation of corresponding angles takes place in geometry when one line crosses two lines This is also called a transversal. The angles which are formed at the corners are at the intersection and are called corresponding angles. They are pairs of one type of angles. corresponding angles can be formed in two ways - through parallel lines and non-parallel lines.
They are of two types of corresponding angles - alternate interior & alternate exterior angles. Corresponding Interior Angles are formed within the corners of the intersection. Corresponding Exterior Angles are formed at the outer corners of the intersecting line. The subtopic “Corresponding Angles Axioms “has been taken from chapter 6 - “Lines & Angles”. The sub-topic carries 3-4 marks and the overall chapter carries 6-8 marks in the CBSE final examinations.
Also Read: Angle between a Line and a Plane
| Table of Content |
Keywords: corresponding angles, geometry, parallel lines, transversal, angles, converse of corresponding angle theorem, congruent angles
Corresponding Angles Definition
[Click Here for Sample Questions]
Corresponding angles are formed when the angels are at the corresponding corner with the transversal line when it is intersected by two parallel lines. If we consider an example given below,

Angle w and angle p are the corresponding angles.
Types of Corresponding Angles
[Click Here for Sample Questions]
In Mathematics, specifically in the case of geometry, we need to learn about different types of lines & angles. Here, we also learn that the corresponding angles are the angles that are formed by the intersection of two lines by a transversal. The two lines can be parallel or non – parallel. Corresponding angles are formed at the opposite sides of the transversal line. Thus, they are of two types:
- Formed by parallel lines & transversal
- Formed by non-parallel lines & transversal
Also Read: Three - dimensional Geometry Introduction
Corresponding Angles formed by Parallel Lines and Transversal
If two parallel lines are crossed by a transversal, the angles formed (corresponding angles) will be of equal measure. Eight angles are formed when parallel lines are intersected by a transversal. Hence, the angle formed on the first line will be equal to the angle formed on the second line by the transversal.
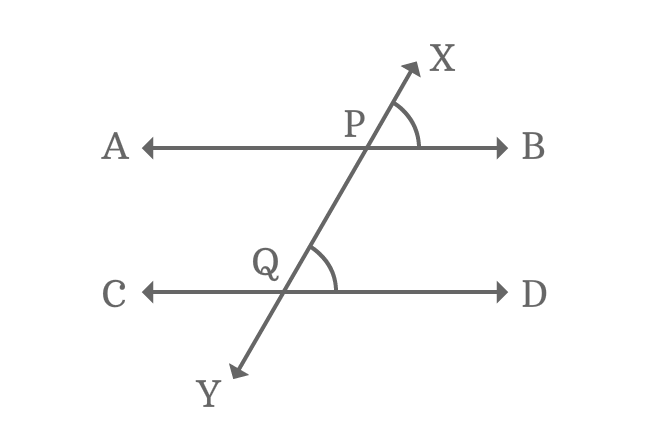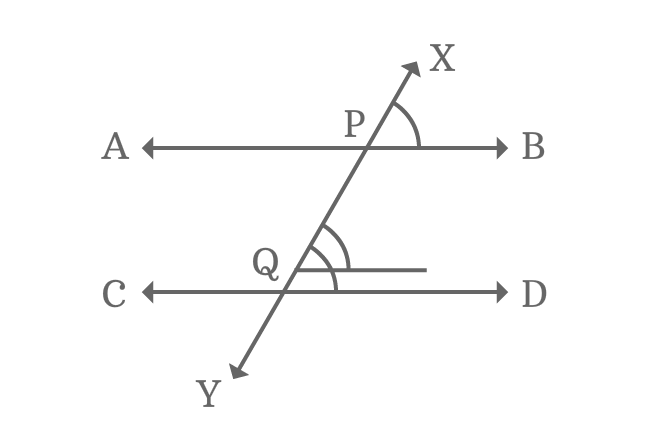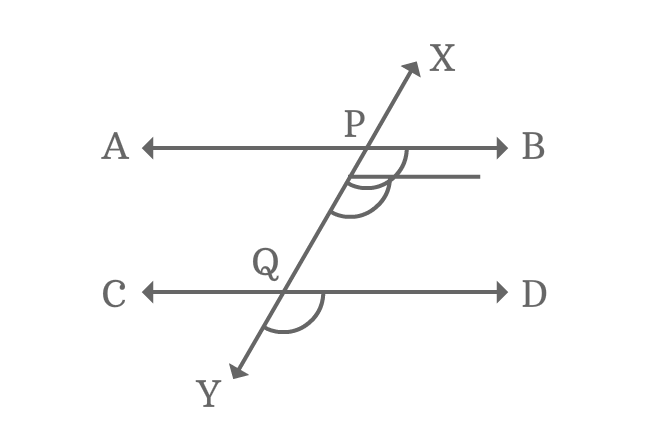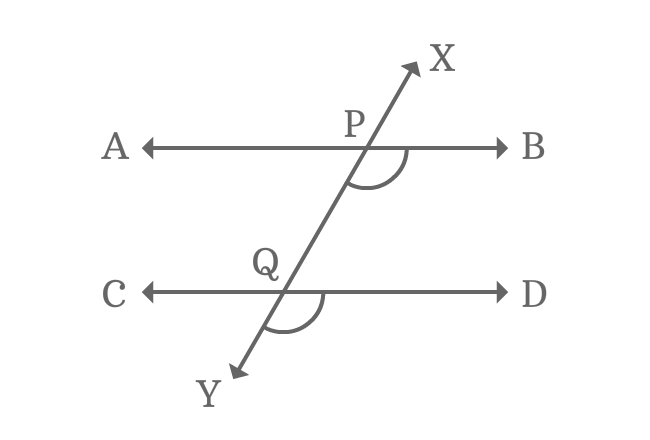
Corresponding Angles formed by Parallel Lines and Transversal
As we know the corresponding angles formed by two parallel lines are equal. So,
- ∠a = ∠e
- ∠b = ∠g
- ∠d = ∠f
- ∠c= ∠h
Corresponding Angles Formed by Non-Parallel Lines and Transversal
When non-parallel lines are intersected by a transversal line, the corresponding angles which are formed have no relation with each other. They are also not equal. Hence, there will also be no relation with the other angles like interior angles or exterior angles, vertically opposite angles, and consecutive angles. We can see this clearly in the diagram given below:
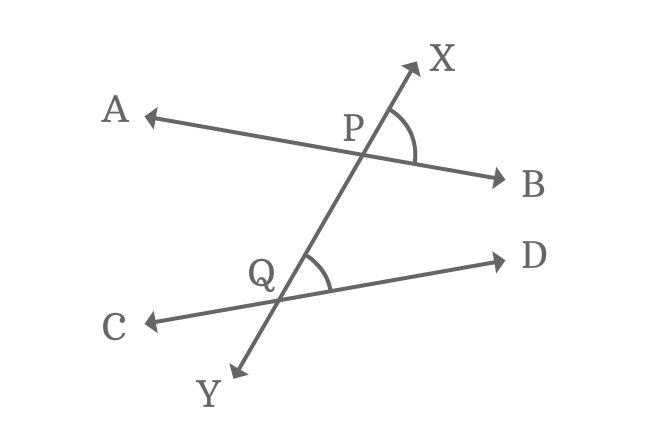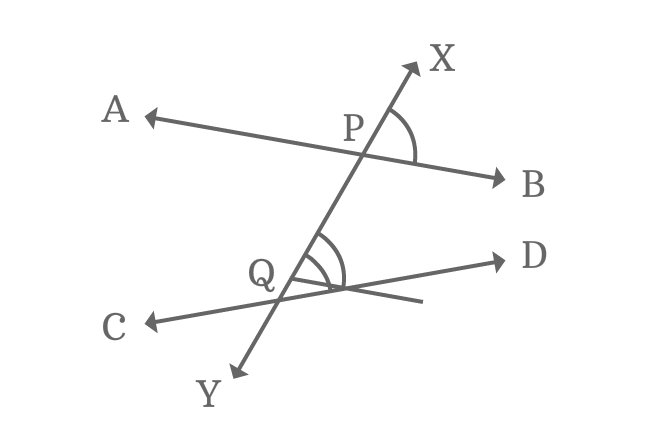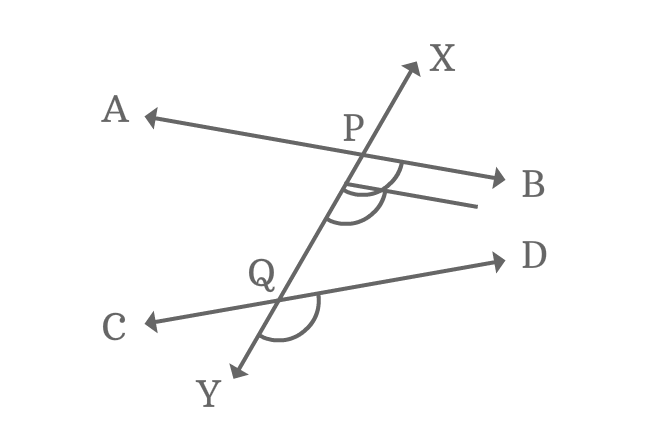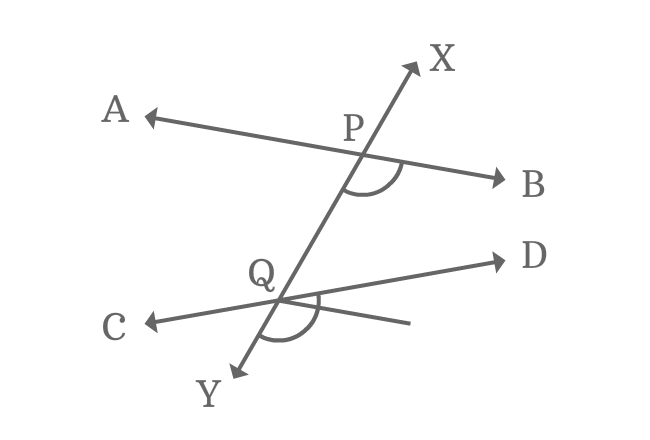
Corresponding Angles Formed by Non-Parallel Lines and Transversal
Corresponding Angles Postulate
[Click Here for Sample Questions]
Using the converse of the Corresponding angles postulates, we can state that- “If corresponding angles created by two lines and a transversal are congruent, then the two lines are parallel.” The Corresponding angles will always remain equal.
Also Read:
| Related Articles | ||
|---|---|---|
| Angle between Two Planes | Angle between Two Lines | |
| Rolle’s Theorem | Equation Line | |
| Sequence and Series | Arithmetic Progression (A.P.) | |
| Mean Value Theorem | Bayes Theorem Formula | |
Corresponding Angles In a Triangle
[Click Here for Sample Questions]
We can obtain corresponding angles in a triangle by obtaining a congruent pair of sides of the two congruent or similar triangles. The Corresponding angles will have the same measure in the case of a triangle as well.
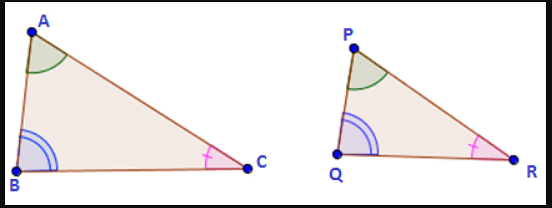
Corresponding Angles In a Triangle
Things to Remember
- Corresponding angles always remain congruent to each other.
- If two parallel lines are intersected by a transversal, the corresponding angles formed are always equal in measure.
- If the corresponding angles formed at the two intersections are congruent, the two lines will then be considered parallel.
- The pair of corresponding angles always lies on the same side of a transversal
- If a transversal intersects two non – parallel lines, all the angles including the corresponding angles will not have any relation to each other.
Sample Questions
Ques: State the Corresponding Angles Axiom or Theorem. (2 Marks)
Ans: If one line intersects two parallel lines, then the angles formed which are correspondent in two points of intersection will be congruent. Hence, the angles will be equal to each other in the case of parallel lines.
Ques: Name the types of corresponding angles on the basis of their sum. (3 Marks)
Ans: On the basis of their sum, the Corresponding angles obtained are:
- Supplementary: If the sum of the pair of angles is 180 degree
- Complementary: If the sum of the pair of angles is 90 degree
Ques: State some examples of a corresponding angle? (3 Marks)
Ans: Examples of a corresponding angle can be:
- Never-ending parallel tracks of the railway line
- Solving a Rubik’s cube
- Opening & shutting of lunchbox
Ques: What is the Converse Corresponding Angle theorem? (2 Marks)
Ans: The converse of corresponding angle theorem states that- if corresponding angles formed at the two different points of intersection are congruent, then the lines are also said to be parallel. Hence the angles will also be equal.
Ques: What are corresponding Interior & Exterior Angles? (2 Marks)
Ans: Corresponding Interior Angles: The angles which are formed within the corners of the intersection
Corresponding Exterior Angles: Angles that are formed at the outer corners of the intersecting line.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Check:





Comments