
Content Curator
Acute angle is a type of angle which measures an angle between 00 to 900. The acute angle is represented by the symbol ‘∠’ and it is measured with the help of a protractor in terms of degree. For example, when the time is 11 o’ clock, the angle formed between the hour hand and the minute hand is considered an acute angle. Also, 350, 450, 580, 890 are all acute angles as their measurement is less than 900.
| Table of Content |
Keyterms: Angle, Degree, Measurement, Traingle, Equilateral triangle, Line segments, Rays
Acute Angle
[Click Here for Sample Questions]
A triangle formed by all angles measuring less than 900 is called an acute-angled triangle. For example in the case of an equilateral triangle, all three angles measure 600, making the equilateral triangle as the acute triangle. Dividing a right angle will give us two or more acute angles as each of the newly formed angles will be less than 900. At least, two angles of any triangle should be acute angles.
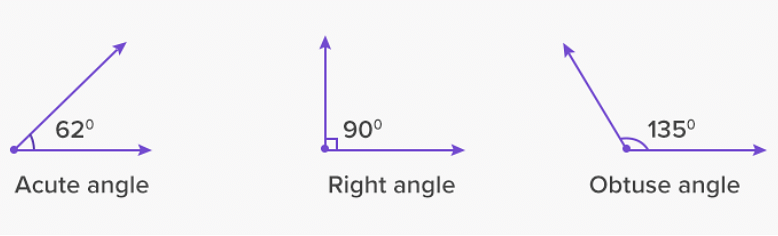
Types of Angles
In an 1800 angle, if one angle is an obtuse (measurement having more than 900 and less than 1800) angle, the other angle will always be the acute angle. An acute angle consists of two rays or line segments. These rays intersect at one endpoint of an acute angle. Acute angles are mainly sharp angles. They are more extreme than a right angle or an obtuse angle.
Read more:
Properties of Acute angles
[Click Here for Sample Questions]
- When all three angles of a triangle are 600, it forms a different kind of triangle called an equilateral triangle.
- Acute triangles can be classified as acute scalene triangles, acute isosceles triangles, and equilateral triangles.
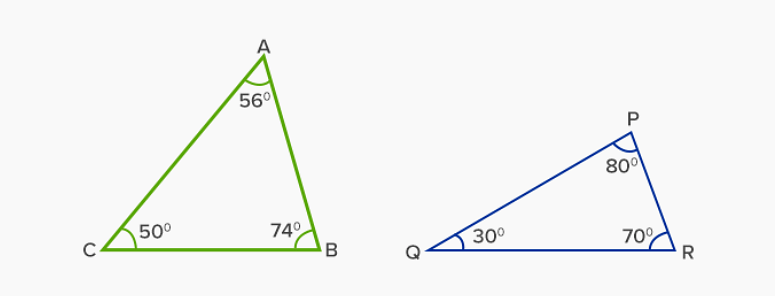
Acute angled triangle
- In an acute angled triangle, the circumcentre lies inside of it.
- In an acute angled triangle, the angle bisector intersects the incentre.
- Two angles of any triangle will be acute angles.
Read more:
Examples of Acute Angles
[Click Here for Sample Questions]
There are many real-life examples of acute angles. Some are listed below -
- If we slice a pizza into 5 or more slices, each slice of pizza will make an acute angle.
- A slice of watermelon when cut in smaller portions makes acute angles.
- The beak of a bird when it is open.
- Acute angle is formed when a crocodile’s mouth is open.

Acute angle examples
- Letter ‘V’ makes an acute angle.
- Few road safety signs show directions that form acute angles.
- Few exercise postures form acute angles.
Read more:
Formula of Acute angle
[Click Here for Sample Questions]
Just like the pythagoras theorem which is for right-angled triangles, we also have an acute angled triangle formula which is known as the triangle inequality theorem for acute angle triangles. It states that the sum of squares of any two sides of a triangle will be greater than the square of the third side.
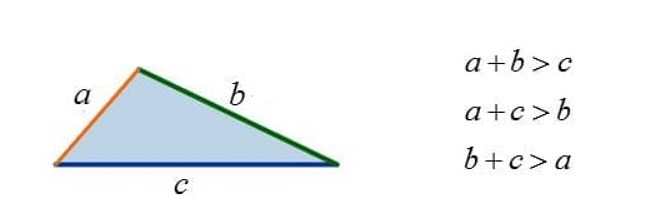
Triangle Inequality Formula
In a Δ ABC, if the sides of a triangle measure “a”, “b”, “c” such that “c” is the largest side, then,
a2 + b2 > c2
In simple words, If a triangle ΔABC satisfies the above condition, then the triangle will be an acute angled triangle.
Read more:
Things to Remember
[Click Here for Sample Questions]
- An apex angle is an angle of a triangle whose two base angles are not congruent.
- If the angle of a triangle is 900, then the circumcentre of the triangle lies outside the triangle.
- The sum of all interior angles of a triangle is equal to 1800, and the sum of all exterior angles of any triangle is equal to 3600.
- Area of a triangle is equal to ½ * base * height.
- Median of a triangle is the line which divides the same triangle into two equal parts.
- Orthocentre, circumcentre, incentre and centroid are the points which coincides at the same point.
- A circumcentre’s radius is always half of its hypotenuse, and the center of the triangle is the hypoteneuse’s midpoint.
Read more:
Sample Questions
Ques. Define the following terms - Line segment, ray, collinear and non-collinear points, angle. (3 Marks)
Ans. Line segment - A line segment is a part of a line which has two endpoints.
Ray - A ray is a part of a line which has only one endpoint.
Collinear and non-collinear points - If three or more points are there on a same line segment, then the points are called collinear points, otherwise points are called non-collinear points.
Angle - An angle is made when two rays originated from the same endpoint.
Ques. Observe the clocks shown below and identify the times at which the hands form an acute angle. (2 Marks)

Ans. From the above given clocks, we can see that the clocks having 10 o’ clock and 11 o’ clock, the angle formed between the hour hand and minute hand is an acute angle. Therefore, the clock 1 and clock 4 make an acute angle.
Ques. What are the different types of angles? (5 Marks)
Ans. Acute angle - An acute angle is an angle which measures less than 900.
Right angle - A right angle is an angle which measures equal to 900.
Obtuse angle - An obtuse angle is an angle which measures more than 90.0 and less than 1800.
Straight angle - A straight angle is an angle which measures equal to 1800.
Reflex angle - A reflex angle is an angle which is more than 1800 and less than 360.0.
Complementary angle - Any two angles whose sum is 900.
Supplementary angle - Any two angles whose sum is 1800.
Adjacent angle - Two angles are said to be adjacent if they have a common vertex, a common arm and their non common arms are on different sides of the common arm.
Vertically opposite angles - These angles are formed when two lines intersect with each other at a point.
Ques. What is a hypotenuse in a right angled triangle? (2 Marks)
Ans. In a right angled triangle, a hypotenuse is the largest side of that triangle which is placed opposite to the 900 angle. Although, all the angles will be less than 900.
Ques. Define the following terms -Circumcentre, Incenter, Centroid, Orthocenter. (5 Marks)
Ans. Circumcenter - A perpendicular bisector is a line segment that divides a side of a triangle in two equal parts. The intersection of the perpendicular bisector of the three sides of an acute angled triangle form a circumcenter.
Incenter - An angular bisector is a line segment that divides an angle of a triangle in two equal parts. The intersection of the angular bisector of the three sides of an acute angled triangle form an incenter.
Centroid - In an acute angled triangle, the median intersects at the centroid of a triangle, and also the centroid always lies inside the triangle.
Orthocenter - An altitude of a triangle is the line that passes through the apex of the triangle and is perpendicular to the opposite side. The three altitudes intersect at the orthocenter.
Ques. Find the area of triangle if the length of one side is 10cm and the corresponding altitude is 30cm. (2 Marks)
Ans. The formula for calculating area of triangle is ½ * base * height.
Given, Base = 10cm, height = 30cm.
Area = ½* 10* 30 = 150 cm2.
Read more:






Comments