
Collegedunia Team Content Curator
Content Curator
Additive inverse is the number, which when added to a number, gives a sum of zero. For example, if we take ‘4’ and add ‘-4’ to it, the net result is 0. Therefore, the additive inverse of 4 is -4. By the same dictum, the additive inverse of -4 is -(-4) = 4. Additive inverse is also known as the opposite number, a sign change or negation. To find out the additive inverse of a number we simply have to change the sign of it or multiply it with -1. The properties of the additive inverse are applicable to all the real numbers as well as the complex or imaginary numbers.
| Table of Content |
Key Takeaways- Additive inverse, complex numbers, multiplicative inverse.
What is Additive Inverse?
An Additive Inverse of a number can be defined as the value, which on adding to the original number gives a net value of zero. Simply put, the additive inverse of a number will be its opposite number. Suppose, if ‘p’ is an original number then its additive inverse will be ‘-p’, such that p+ (-p)=0.
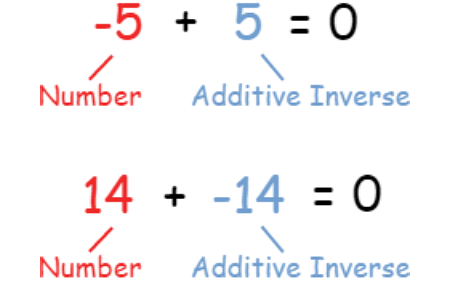
Additive Inverse
We can determine the additive inverse for the real numbers as well as complex numbers. The simple rule to find an additive inverse is to change a positive number to the negative number of the same value or vice-versa.
Also Read:
General Formula of Additive Inverse
To find an additive inverse we have to find the opposite number of the number given. The general formula of the additive inverse is as follows.
Additive Inverse of a number = (-1) x number
For example, if we want to find the additive inverse of the number 50, we will simply multiply (-1) with it.
Additive inverse of 50 = (-1) x 50 = -50
If we want to find out the additive inverse of -60, we can apply the same rule.
Additive inverse of -60 = (-1) x (-60) = 60
Also Read: Permutations and Combinations
Properties of Additive Inverse
Here are some properties of Additive Inverse, based on the negation of the original number. If p is the original number, then its additive inverse will be -p, we will see the properties of -p as follows.
- −(−p) = p
- (-p)2 = p2
- −(p + q) = (−p) + (−q)
- −(p – q) = q − p
- p − (−q) = p + q
- (−p) × q = p × (−q) = −(p × q)
- (−p) × (−q) = p × q
These additive inverse properties hold good for the real numbers as well as complex numbers.
Additive Inverse of Real Numbers
The given number can be a whole number, a natural number, a fraction, a decimal. An integer or any other real number. The additive inverse of that real number is just the negative of the given number. The above-mentioned properties also apply.
| Real Numbers | Number | Additive inverse | Outcome |
|---|---|---|---|
| Natural Numbers | 13 | -13 | 13 + (-13) = 0 |
| Whole Numbers | 6 | -6 | 6 + (-6) = 0 |
| Integers | 5 | -5 | 5 + (-5) = 0 |
| Fractions | 1/3 | -1/3 | ? + (-1/3) = 0 |
| Decimals | 6.5 | -6.5 | 6.5 + (-6.5) = 0 |
Also Read:
Additive Inverse of Complex Numbers
The complex numbers are the combinations of the real numbers and imaginary numbers, described in the form of,
A+iB
where,
A → Real Number
iB → Imaginary Part
The algebraic property of complex numbers shows the existence of their additive inverse.
For example, if any given complex number z? C, there will be a unique complex number, maybe denoted by -z, such that z + (-z) = 0. Moreover, if z = (p,q) and p,q ? R, then -z= (-p,-q).
Let z = p + iq be the given complex number. Then the inverse of it will be -z = -p - iq.
Thus, the additive inverse will be,
z + (-z) = p + iq - p - iq = 0
Also Read:
Additive Inverse of a Fraction
The general rule of the additive inverse applies to fractions as well. For example, the additive inverse of a fraction p/q is –p/q and vice-versa. It is because,
p/q + (-p/q) = 0
So, the additive inverse of a positive fraction will be the same fraction with a negative sign, while for a negative fraction, its additive inverse will be the same fraction without a negative sign i.e., a positive sign.
Additive Inverse and Multiplicative Inverse
In mathematics, there are two properties of numbers: additive inverse and multiplicative inverse properties related to addition and multiplication operation respectively. For a number p, -p is the additive inverse and 1/p is the multiplicative inverse. The comparison between the two is tabulated below.
| Additive Inverse | Multiplicative Inverse |
|---|---|
| To get the additive inverse we change the sign of a number or multiply it with -1. | To obtain the multiplicative inverse we multiply the number with its reciprocal |
| The ultimate outcome of adding an additive inverse to the original number is 0. | The outcome of multiplying a multiplicative inverse to its original number is 1. |
| Formula: p+(-p)=0 | Formula: p*1/p=1 |
Things To Remember
- The additive inverse of a number is a value that gives a net outcome of zero when added to the original number.
- The additive inverse of a number will be the opposite number of it which simply means it will have the opposite sign.
- The formula to find the Additive Inverse of a number ‘p’ will be (-1) x p.
- The general principles of additive inverse apply to both real numbers and complex numbers.
- Additive inverse and multiplicative inverse are two different things. In the case of Additive Inverse, we find the opposite number of an original number by changing its sign such that the sum total of two is always zero. On the other hand, the multiplicative inverse, we take the reciprocal of the number.
Also Read:
Sample Questions
Ques: What is Additive inverse? (2 marks)
Ans: By definition, an Additive Inverse of a number is the value, which on adding to the original number gives a net sum of zero. In simpler terms, the additive inverse is the opposite number of the given number.
Ques: State the formula for finding the additive inverse of a number. (2 marks)
Ans: The formula for finding the additive inverse of a given number is
Additive inverse of the number= (-1)*given number.
Ques: What is the additive inverse of 45? (2 marks)
Ans: Let X be the additive inverse of 45.
So as per the rule, 45+X=0→ X=-45
Thus, the additive inverse of 45 is -45.
Ques: Find out the additive inverse and multiplicative inverse of the number 100. (2 marks)
Ans: To find out the additive inverse of 100 we can multiply it with (-1). So, the additive inverse of the number 100 will be -100.
To find out the multiplicative inverse we would take the reciprocal of the number 100. Thus, the multiplicative inverse of 100 is 1/100.
Also Read: Types of Probability
Ques: State any three properties of the additive inverse. (2 marks)
Ans: Three additive properties of additive inverse are-
- −(−p) = p
- (-p)2 = p2
- −(p + q) = (−p) + (−q)
(Where p and q are two real numbers)
Ques: What is the difference between additive inverse and multiplicative inverse. (2 marks)
Ans: Additive Inverse simply refers to the value of a number that gives a sum of zero when added to the original number. For example, if ‘A’ is a real number, the additive inverse of ‘A’ will be ‘-A’.
On the other hand, to find out the multiplicative inverse we need to find out the reciprocal of that number which upon multiplication with that number gives 1. For example, for a real number ‘A’, its multiplicative inverse will be ‘1/A’.
Ques: Do the properties of the additive inverse apply to complex numbers as well? (2 marks)
Ans: Yes. The properties of additive inverse apply to complex numbers as well. For example, a complex number z= p+iq, the inverse of it will be -z=-p-iq.
Also Read:
Ques: What is the additive inverse of the expression 14x-34y+5z? (2 marks)
Ans: Let us assume the additive inverse of the expression 14x-34y+5z is A.
So according to the formula, 14x-34y+5z+A=0 →A = -14x+34y-5z.
Therefore, the additive inverse of the expression will be -14x+34y-5z.
Ques: Find out the additive inverse of the fraction 6/19. (2 marks)
Ans: The additive inverse of the fraction 6/19 is -6/19.
Ques. The negative of the negative of any rational number is the number itself. State whether true or false. (2 marks)
Ans. True.
Let x be a positive rational number. Then, -x be a negative rational number.
Now, negative of negative rational numbers = -(-x)= x = Positive rational number.
Also Read: Pascal’s Triangle
Ques. If x + y = 0, then -y is known as the negative of x, where x and y are rational numbers. State whether true or false. (2 marks)
Ans. False.
If x and y are rational numbers and x+ y = 0.
Then, y is known as the negative of x.
Ques. The rational numbers −1/2 and -1 are on the opposite sides of zero on the number tine. State whether true or false. (2 marks)
Ans. True
Since, positive rational numbers and negative rational numbers are on the opposite sides of zero on the number line.’
Hence, −1/2 and -1 are on the opposite sides of zero on the number line.
Also Read:







Comments