
Content Curator
Isosceles right triangle is a two dimensional three sided figure in which one angle measures 90°, and the other two angles measure 45° each. In an isosceles right triangle, Hypotenuse is given by formula H=B\(\sqrt{2}\), the area is given by B2/2, and perimeter is given by 2B+H. [H-hypotenuse, B-any of the other two sides].
| Table of Content |
Key Takeaways: Triangle, Isosceles triangle, Isosceles right triangle, Hypotenuse, Area, Perimeter.
Triangle
In geometry, a triangle is a two-dimensional figure with three sides and three angles.
The summation of the three angles of any triangle is always 180°.
The sum of the two sides of any triangle (in isosceles right triangle too) is always greater than the third side.
Types of Triangles
According to the measure of angles in a triangle, the triangles can be:
- Acute
- Obtuse
- Right
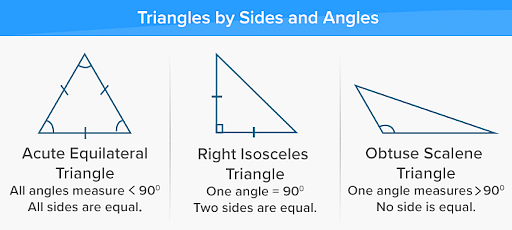
According to the length of sides in a triangle, triangles can be:

According to both angles and sides in a triangle, the triangle can be:
- Right equilateral
- Right isosceles
- Obtuse Scalene

Also Read:
Isosceles triangle
A triangle in which the length of two of its sides is equal is called an isosceles triangle. Since the length of two sides of the isosceles triangle is equal, the corresponding angles are equal to each other too.

Here, side AC=BC; and angle ∠CAB= ∠CBA
The unequal side (AB) of an isosceles triangle is usually referred to as the 'base' of the triangle.
Right triangle
Right angle triangle is a triangle in which one angle is 90°. The longest side of the right triangle is the hypotenuse and the other two sides are height and the base. The opposite side (BC) of the right angle, whose ends are touched by arms of the angle (AB & AC), is the hypotenuse.
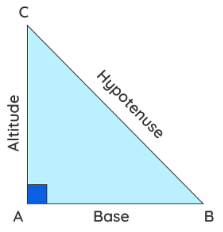
AC ⊥ AB
∠A=90º
Also Read:
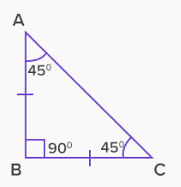
Isosceles right triangle
A triangle in which one angle measures 90°, and the other two angles measure 45° each is an isosceles right triangle. In an isosceles right triangle (figure below), ∠A and ∠C measure 45° each, and ∠B measures 90°. The sides AB and AC are equal. This type of triangle is also known as a 45-90-45 triangle
AC, the side opposite of ∠B, is the hypotenuse. And AB or AC can be taken as height or base
Also Read: Quadrilateral
Formulas
Given below are the formulas to construct a triangle which includes:
- Pythagoras theorem
- Area
- Perimeter
Pythagoras Theorem
Pythagoras theorem, which applies to any right-angle triangle, also applies to isosceles right triangles.
In an isosceles right triangle, the length of base (BC) is equal to length of height (AB). If base (BC) is taken as ‘B’, then AB=BC=’B’. Let the hypotenuse be taken as ‘H’
Pythagoras theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the square of the other two sides.
(Hypotenuse)2 = (Side)2 + (Side)2
H2=B2+B2
H2=2B2
H=B\(\sqrt{2}\)
Area
The area of a triangle is half of the base times height.
Area = ½ × b × h
Here, b-base; h-height
This applies to right isosceles triangles also.
As stated above, in an isosceles right-triangle the length of base (BC) is equal to length of height (AB). If, base (BC) is taken as ‘B’, then AB=BC=’B’
Area of right isosceles triangle= ½ ×B×B
= B2/2
Perimeter
The Sum of all sides of a triangle is the perimeter of that triangle.
In the right isosceles triangle, since two sides (Base BC and Height AB) are same and taken as ‘B’ each. And the hypotenuse is taken as ‘H’.
The perimeter= AB+BC+AC
= B+B+H
=2B+H
Also Read:
Things to Remember
- Triangles are polygons with the least number of sides; since any figure with two sides only forms an angle.
- In the right triangle two sides are perpendicular to each other; in the right isosceles triangle these two sides are of equal length.
- The difference between any two sides is smaller than the
- third side-AB-BC<AC
- The concept of right isosceles triangles is used by architects. Even Egyptians used these to design pyramids.
Sample Question
Ques: Find the length of the other two sides of the isosceles right triangle given below: (2 marks)
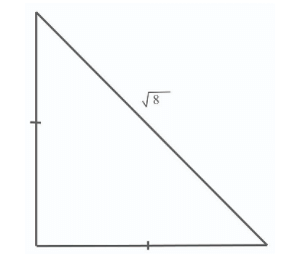
Ans: We know the length of the hypotenuse is \(\sqrt{2}\), we need to determine the lengths of the other two sides.
Because the length of the hypotenuse is \(\sqrt{2}\) times the length of the other sides, we can construct by using Pythagoras theorem for isosceles right triangle- H2=2B2
H2=2B2
H=B2
B=H\(\sqrt{2}\)
x=\(\frac{\sqrt{8}}{\sqrt{2}}\)
x=\(\sqrt{4}\)=2
So, the length of the other two sides is 2 units each.
Ques: The lengths of sides of an isosceles right triangle measure x=14cm. Find its perimeter. (2 marks)
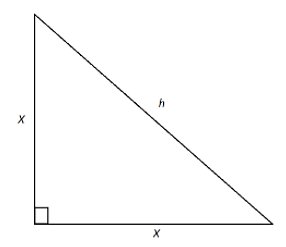
Ans: For an isosceles right triangle,
H=B\(\sqrt{2}\)
H= x\(\sqrt{2}\)
H=14\(\sqrt{2}\) cm
Now the perimeter= 2B+H
P= (142) +19.80
P=47.8cm
So, the perimeter of the given triangle is 47.8cm.
Ques: A triangle has two angles are 450 and two sides equal to 8. What is the perimeter of this triangle? (2 marks)
Ans: When a triangle has two angles equal to 450, it must be a 450:450:900 isosceles right triangle.
Since two sides are 8.
The hypotenuse= 8\(\sqrt{2}\) [using H=B\(\sqrt{2}\), obtained from Pythagoras theorem]
Perimeter= 2B+H= 8+8+8\(\sqrt{2}\) =16+ 8\(\sqrt{2}\)
So, the perimeter is 16+ 8\(\sqrt{2}\) units.
Ques: An isosceles right triangle has hypotenuse of h=18\(\sqrt{2}\) inches. Find its area. (3 marks)
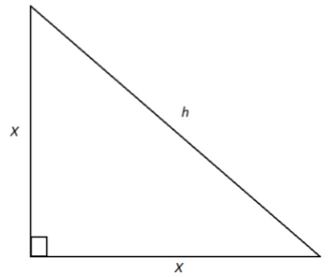
Ans: To calculate the triangle's area, we need to find the lengths of its sides. Hypotenuse is given
H=B\(\sqrt{2}\)
B=\(\frac{H}{\sqrt{2}}\)
B=\(\frac{18 \sqrt{2}}{\sqrt{2}}\)
B=18 inches
Two sides of the right isosceles triangles are 18 inches each.
Now, area of right isosceles triangles:
Area= B2/2
=182/2
Area =162 inch2
Ques: What are the different kinds of triangle? (3 marks)
Ans: Triangles can be classified according to the measure of angles, of sides, and of both sides, angles taken together-
According to measure of angles in triangle, the triangles can be- 1) Acute 2) Obtuse 3) Right
According to length of sides in triangle, triangles can be- 1) Equilateral 2) Isosceles 3) Scalene
According to both angles and sides in triangle, triangle can be- 1) Right equilateral 2) Right isosceles 3) Obtuse Scalene
Ques: The equal sides of an isosceles right triangle are 8 units each. Find the area. (2 marks)
Ans: For an isosceles right triangle,
the area formula = B2/2
Here, B = 8 units
Thus, Area = 82/2 = 32 square units
Thus, the area of the isosceles right triangle is 32 sq units.
Ques: The perimeter of an isosceles right triangle is 10 + 5\(\sqrt{2}\) units. If the hypotenuse measures 5\(\sqrt{2}\) units then, find the measure of the other sides. (2 marks)
Ans: For an isosceles right triangle, the perimeter formula is given by 2B+H
Here, H = 5\(\sqrt{2}\)units, Perimeter (P)= 10 + 5\(\sqrt{2}\) units
By using the formula,
P= 2B+ H
10 + 5\(\sqrt{2}\)=2B+ 5\(\sqrt{2}\)
B=5
Hence, the length of the other side is 5 units each.






Comments