
Collegedunia Team Content Curator
Content Curator
Properties of parallel lines include transitive and symmetric property among many others. Parallel Lines are the lines that are non-intersecting with each other. Lines parallel to each other are straight lines that remain at the same distance from one another at all points. They hence do not meet one another irrespective of their length in either direction. Two lines are said to be parallel when they are drawn in the same plane. The length of similar perpendiculars at all points on these parallel lines is equal. This equal length is known as the distance between two parallel lines.
Also Read : Horizontal and Vertical Lines
| Table of Content |
Key Terms: Parallel Lines, Properties, Transitive, Symmetric Property, Transversal, Corresponding Angles, Exterior Angles
Properties of Parallel Lines
[Click Here for Sample Questions]
The following are the general properties of parallel lines:
- The distance between two parallel lines is equal at all points.
- If a straight line is parallel to a pair of lines, then all three lines are parallel to each other.
- Two lines are parallel when they are in the same plane and are perpendicular to the same line.
- Only a single parallel line can be drawn parallel to a particular line through a particular point that is not located on the same line.
Some of the other interesting properties of parallel lines are as follows:
- Transitive Property of Parallel Lines
- Symmetric Property of Parallel Lines
- Property of Parallel lines cut by a transversal
Let us look at each of the properties of parallel lines in detail with the help of figures.
Also Read: Angle Formula
Transitive Property of Parallel Lines
[Click Here for Sample Ques ons]
Two lines which are parallel to the same line are parallel to one another. This property of parallel lines is alluded to as the transitive property of equal lines. The property holds good for multiple lines.
Therefore, if line l is corresponding to line m and line m is corresponding to line n then, then, line l is corresponding to line n.

Transverity of Parallel Lines
Also Read: Parallel Lines and a Transversal
Symmetric Property of Parallel Lines
[Click Here for Sample Questions]
Symmetric property of parallel lines expresses that if line 1 is parallel to line 2, then line 2 is also parallel to line 1.
In the figure below, line a is parallel to line b. By the symmetric property of parallel lines, we can say that line b is also parallel to line a.
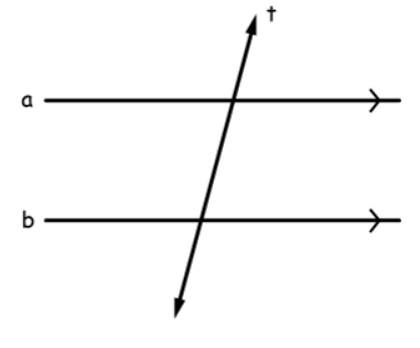
Symmetric Property of Parallel Lines
Also Read: Transversal and Angles
Properties of Parallel Lines Cut by a Transversal
[Click Here for Sample Questions]
Given below are the properties of parallel lines when cut by a transversal:
- When two lines are cut by a transversal such that the corresponding angles so formed are equal, then the two lines are parallel.

Corresponding Angles
- When two lines are cut by a transversal such that the alternate interior angles so formed are equal, then the two lines are parallel.

Alternate Interior Angles
- When two lines are cut by a transversal such that the alternate exterior angles so formed are equal, then the two lines are said to be parallel.

Alternate Exterior Angles
Also Read: Types of Angles
Things to Remember
[Click Here for Sample Questions]
- Parallel lines are equidistant from each other throught their length.
- Two or more lines parallel to the same line are parallel to one another.
- Symmetric property of parallel lines expresses the parallel nature of two or more parallel lines with each other.
- When a two parallel lines are cut by a transversal:
- The corresponding angles are equal.
- The vertically opposite angles are equal.
- The alternate interior and alternate exterior angles are equal.
- Two interior angles when on the same side of the transversal are supplementary.
Also Read: Area of a Parallelogram
Sample Questions
Ques. In the following figure m, n and l are parallel lines and AB is parallel to CD. Find the value of x using the given angles. (3 marks)

Ans.Since m || l, ∠CGI = 120° (Corresponding angles)
∠FGC = 180° – 120° = 60° (Linear pair with ∠CGI)
∠BIH = ∠BFE = 40° (Corresponding angles)
∠BFE = ∠GFC = 40° (Vertically opposite angles)
Therefore, from the above properties of parallel lines,
x + 40° + 60° = 180° (Sum of angles of a triangle is 180°)
Or x = 180° – 100° = 80°
Ques. In the given figure, if PQ || RS, ∠ MXQ = 135° and ∠ MYR = 40°, find ∠ XMY (3 marks)

Ans. Let AB|| PQ through M point
Since PQ || RS
therefore AB || RS
Since AB || PQ and MX is the transversal
Since ∠ XMB = 45°
now ∠ BMY = ∠ MYR (AB || RS, Alternate angles)
Therefore, from the above properties of parallel lines,
∠ BMY = 40°
Adding ∠ XMB + ∠ BMY = 45° + 40°
That is, ∠ XMY = 85°
Ques. If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. (3 marks)

Ans. A traversal AD intersects two lines PQ and RS at points B and C respectively. Ray BE is the bisector of ∠ ABQ and ray CG is the bisector of ∠ BCS, and BE || CG
We are to prove that PQ || RS.
It is given that ray BE is the bisector of ∠ ABQ
Therefore, ∠ ABE = 1/ 2 ∠ ABQ
Similarly, ray CG is the bisector of ∠ BCS.
Therefore, ∠ BCG = 1 /2 ∠ BCS
But BE || CG and AD is the transversal
Therefore, from the above properties of parallel lines,
∠ ABE = ∠ BCG (Corresponding angles axiom)
Thus 1/ 2 ∠ ABQ = 1 /2 ∠ BCS
That is, ∠ ABQ = ∠ BCS
But, they are the corresponding angles formed by transversal AD with PQ and RS; and are equal. Therefore, PQ || RS (Converse of corresponding angles axiom)
Ques. In the given figure AB || CD and CD || EF. Also EA ⊥ AB. If ∠ BEF = 55°, find the values of x, y and z. (2 marks)

Ans. Given AB || CD and BE is the transversal
So x= y (corresponding angles) (1)
Also, CD || EF and BE is the transversal
Therefore, from the above property of parallel lines,
y + 55 degrees = 180 degrees
y = 180 -55
y = 125 degrees
from (1) x = 125 degrees
Ques. in the given fig, find the values of x and y and then show that AB || CD. (2 marks)

Ans. We know that a linear pair is equal to 180°.
So, x+50° = 180°
∴ x = 130°
We also know that vertically opposite angles are equal.
So, y = 130°
In two parallel lines, the alternate interior angles are equal. In this
x = y = 130°
Thus from the above properties of parallel lines, it proves that alternate interior angles are equal and so, AB ||CD.
Ques. In the given fig if AB || CD , CD || EF and y:z = 3: 7 , find x. (4 marks)

Ans. It is known that AB ||CD and CD||EF
As the angles on the same side of a transversal line sums up to 180°,
x + y = 180° —–(i)
Also,
O = z (Since they are corresponding angles)
y +O = 180° (Since they are a linear pair)
So, y+z = 180°
let y = 3w and hence, z = 7w (As y : z = 3 : 7)
From the above property of parallel lines,
∴ 3w+7w = 180°
Or, 10 w = 180°
So, w = 18°
Now, y = 3×18° = 54°
and, z = 7×18° = 126°
Now, angle x can be calculated from equation (i)
x+y = 180°
Or, x+54° = 180°
∴ x = 126°
Ques. In the given fig if AB || CD EF ⊥ CD and ∠ GED = 126°, find ∠ AGE, ∠ GEF and ∠ FGE. (4 marks)

Ans. Since AB ||CD, GE is a transversal.
It is given that GED = 126°
So, GED = AGE = 126° (As they are alternate interior angles)
Also,
GED = GEF +FED
As EF⊥ CD, FED = 90°
From the above properties of parallel lines,
∴ GED = GEF+90°
Or, GEF = 126° – 90° = 36°
Again, FGE +GED = 180° (Transversal)
Putting the value of GED = 126° we get,
FGE = 54°
So,
AGE = 126°
GEF = 36° and
FGE = 54°
Ques. In the given figure if AB || CD , APQ =50 degrees and PRD = 127 degrees , find x and y. (4 marks)

Ans. From the diagram,
APQ = PQR (Alternate interior angles)
Now, putting the value of APQ = 50° and PQR = x we get,
x = 50°
Also,
APR = PRD (Alternate interior angles)
Or, APR = 127° (As it is given that PRD = 127°)
From the above property of parallel lines, we know that
APR = APQ+QPR
Now, putting values of QPR = y and APR = 127° we get,
127° = 50°+ y
Or, y = 77°
Thus, the values of x and y are calculated as:
x = 50° and y = 77°
Ques. In the given Fig, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD. (4 marks)

Ans. First, draw two lines BE and CF such that BE ⊥ PQ and CF ⊥ RS.
Now, since PQ || RS,
So, from the above property of parallel lines, BE || CF
We know that,
The angle of incidence = Angle of reflection (By the law of reflection)
So,
1 = 2 and
3 = 4
We also know that alternate interior angles are equal. Here, BE ⊥ CF and the transversal line BC cuts them at B and C
So, 2 = 3 (As they are alternate interior angles)
Therefore, from the above property of parallel lines,
1 +2 = 3 +4
Or, ABC = DCB
So, AB ||CD (alternate interior angles are equal)
Important Links:






Comments