
Content Writer
The area of a kite is based on the design of a kite. A kite is a quadrilateral with four non-collinear joined points, giving a closed quadrilateral with four sides.
- In a kite, two pairs of adjacent sides are equal.
- It has 4 (four) sides, 4 (four) vertices, and 4 (four) angles.
In other words, the area of a kite can be defined as the amount of space encompassed or enclosed by a kite in a two-dimensional plane. Like a square and a rhombus, a kite does not have all four sides equal.
- Moreover, the area of a kite is always represented by units2, for instance, in2, cm2, m2, and so on.
- Diamond rings and stained glass windows resemble the shape of a kite.
- Thus, we can calculate the area of diamond and stained glass windows.
- The area of the kite can mathematically represented as:
[d1×d2]/ 2
Key Terms: Area of a kite, Kite, Quadrilateral, Diagonal, Right Angles, Isosceles Triangles, Congruent Triangles, Area of Triangles, Non-Collinear, Common Base.
Properties of a Kite
[Click Here for Sample Questions]
The properties of kite are as follows:
- First and foremost, the property of a kite includes opposite angles, which are equal between unequal sides.
- A kite is a quadrilateral, with each pair of adjacent sides equal and congruent.
- The opposite sides of a kite are not equal and not congruent.
- A kite is shaped with a pair of two congruent triangles with a common base.
- Both of the diagonals of a kite intersect each other at right angles (90o).
- The diagonals are bisecting each other perpendicularly.
- The longer diagonal divides the kite symmetrically.
- Kite is divided into two isosceles triangles by the smaller diagonal.
Also Read:
| Related Articles | ||
|---|---|---|
| First Order Differential Equation | Difference Between Variance and Standard Deviation | Congruence of Triangles |
Area of a Kite
[Click Here for Sample Questions]
The area of a Kite includes the amount of space encompassed by a kite on a two-dimensional plane. The kiting area is always mentioned in terms of units2, for example, in2, cm2, m2, etc.
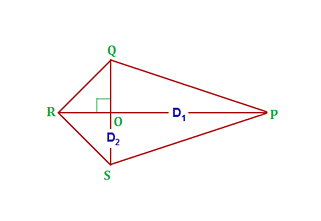
- The below figure is a quadrilateral ABCD, AB, BC, CD, and DA are the four sides.
- B, C and D are four vertices.
- A, B, C and D are the four angles formed at vertices.
- After joining the opposite vertices, A to C and B to D, AC and BD 2 (two) diagonals are formed in quadrilateral ABCD.
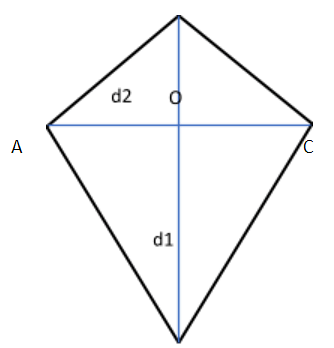
- The area of a kite is half of the product of the diagonals.
- Its area is equivalent to the area of rhombus.
Area of a Kite = 1/2 × d1 × d2
where,
- d1: shorter diagonal of the kite
- d2: longer diagonal of the kite
Area of a Kite
Example of Area of a KiteExample: Four friends are flying kites of the same size in a park. The lengths of diagonals of each kite are 10 in and 20 in. Determine the sum of areas of all the four kites. Solution: Lengths of diagonals are: (d)1 =10in (d)2 =20in The area of each kite is: A = ½ × (d)1 × (d)2 Since each kite is of the same size, therefore the total area of all the four kites is 4 × 100 = 400in2. |
Area of a Kite Formula
[Click Here for Sample Questions]
Area of a kite formula include the product of the lengths of its two diagonals which is divided by 2. To determine the area of a kite, we need to determine the values of the diagonals.
- The formula for area of a kite is:
Area of a Kite = ½ (D1 x D2)
Where
- D1- Long Diagonal and D2–Short Diagonal of the kite.
Example of Area of a Kite FormulaExample: Reema wants to give a kite-shaped chocolate box to her friend. She wants to paste a picture of herself with her friend to cover the top of the box. Determine the area of the top of the box if the diagonals of the lid of the box are 19 in and 20 in. Solution: (d)1 = 19in (d)2 = 20in Since the box is kite-shaped, therefore the area of the top of the box is: A = ½ × (d)1 × (d)2 = 190 |
Derivation of Area of a Kite
[Click Here for Sample Questions]
To derive the area of a kite follows the below steps:
- Consider BD = Long diagonal and AC = Short diagonal
- In the Figure given below, Let ABCD is a kite.
Let, the long diagonal BD = d1 and the short diagonal AC = d2,
- AC = AO +OC = d2
Area of kite ABCD = Area of ΔABD + Area of ΔBCD... (1)
- We know that,
- Triangle's Area = ½ × Base × Height
- Now, we will calculate the areas of triangles ABD and BCD
- Area of ΔABD = ½ × AO × BD = ½ × AO × d1
- Area of ΔBCD = ½ × OC × BD = ½ × OC × d1
- Therefore, using (1),
- Area of kite ABCD = ΔABD + ΔBCD
- i.e ΔABCD= ½ × AO × d1 + ½ × OC × d1
- ½× d1 x (AO + OC)
- ½ × d1 x d2
- Therefore,
Δ ABCD = ½ × d1 x d2
Thus, when the length of the diagonal values are given, we need to just multiply both the diagonal value and divide them by 2, to get the area of the kite.
Things to Remember
- Area of kite is equal to the product of diagonals divided by two.
- The area is enclosed by a kite.
- A kite is a quadrilateral that has four sides, four vertices and four angles.
- In the figure, adjacent sides are equal and are congruent.
- Like a square and a rhombus, it does not have all four sides equal.
- Both of the diagonals of a kite intersect each other at right angles (90o).
- The diagonals are bisecting each other perpendicularly.
Read More:
Sample Questions
Ques: In a park, four buddies are flying identical kites. Each kite's diagonals are 12 inches and 15 inches long. Calculate the total area of all four kites. (2 marks)
Ans: Diagonal lengths are:
d1=12in
d2=15in
So The area of each kite is:
A = ½ ×d1×d2
= ½ × 12 × 15
= 90 in2
Because each kite is the same size, the total area of all four kites is 4 90 = 360in2.
As a result, the four kites have a total area of 360in2.
Ques: Kate wants to offer her buddy a kite-shaped chocolate box. She wants to cover the top of the box with a photo of herself and her friend. If the lid of the box has diagonals of 9 in and 12 in, calculate the area of the top of the box. (2 marks)
Ans: d1 = 9in
d2 =12in
Because the box is kite-shaped, the top of the box has the following area:
A = ½ ×d1×d2
= ½ × 9 × 12
As a result, the top of the box has a 54in2 area.
Ques: Find the area of a kite if one diagonal is 2cm long, and the other diagonal is 10cm long. (2 marks)
Ans: The formula for the area of a kite is: A= ½ x d1 x d2
Plugin the values for each of the diagonals and solve.
A= ½ x 2x 10= 20/2 =10cm2
Ques: Find the area of a kite with the diagonal lengths of 2a and 2b. (2 marks)
Ans: Find the area of a kite using its formula. Replace with the diagonals and solve.
A = ½ x d1 x d2
=2a x 2b/2=2ab
Ques: Find the area of a kite if the diagonals of the kite are √8, √7. (3 marks)
Ans: You find the area of a kite by using the lengths of the diagonals.
A= ½ x d1×d2
A=√8 ×√7/2, which is equal to √56/2.
You can reduce this to,
√2 x 4 x 7 /2 = 2 x √2 x 7/2=√2 x 7 =√14 for the ultimate answer.
(3,4,5)
Ques: A kite's diagonals intersect to form four segments of 6 metres, 4 metres, 5 metres, and 4 metres. What is the size of the kite's area. (3 marks)
Ans: The 4 metre and 4 metre segments must represent the segment that was bisected into two equal portions or d2.
Therefore,
d2 = 4 + 4 = 8 meters
The segments with lengths 6 meters and 5 meters must represent d1 then
d1 = 6 meters + 5 meters = 11
Area of a kite = ½ (d1 x d2)
= (8 × 11) / 2
= 88 / 2
= 44 square meters
Ques: A kite has a 126 cm2 area and a diagonal that is 21 cm long. Determine the opposite diagonal's length. (3 marks)
Ans: Provided,
A kite's area is 126 cm2.
One diagonal is 21 cm long.
Area of a kite = ½ (d1 x d2)
=1/2x 126x21
D2 = 12cm
Ques: A kite's diagonals intersect to form four segments of 7 metres, 4 metres, 5 metres, and 5 metres. What is the size of the kite's area. (3 marks)
Ans: The 4 metre and 5 metre segments must represent the segment that was bisected into two equal portions or d2.
Therefore,
d2 = 4 + 5 = 9 meters
The segments with lengths 7 meters and 5 meters must represent d1 then
d1 = 7 meters + 5 meters = 12
Area of a kite = ½ (d1 x d2)
= (9 × 12) / 2
= 108 / 2
= 54 square meters
Ques: A kite has a 225 cm2 area and a diagonal that is 30 cm long. Determine the opposite diagonal's length. (3 marks)
Ans: Provided,
A kite's area is 225 cm2.
One diagonal is 30 cm long.
Area of a kite = ½ (d1 x d2)
225 =1/2x d1 x 30
D2 = 15 cm
Ques: Find the area of a kite if one diagonal is 4cm long, and the other diagonal is 30cm long. (2 marks)
Ans: The formula for the area of a kite is: A= ½ x d1 x d2
Plugin the values for each of the diagonals and solve.
A= ½ x 4x 30= 120/2 =60cm2
Ques: Find the area of a kite with the diagonal lengths of 4a and 4b. (2 marks)
Ans: Find the area of a kite using its formula. Replace with the diagonals and solve.
A = ½ x d1 x d2
=4a x 4b/2=8ab
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Check:





Comments