Content Curator

An equilateral triangle is a triangle with equal sides and equal angles. All the internal angles are of the measure 60º. The word ‘equi’ comes from Latin and means “equal” or “the same”.

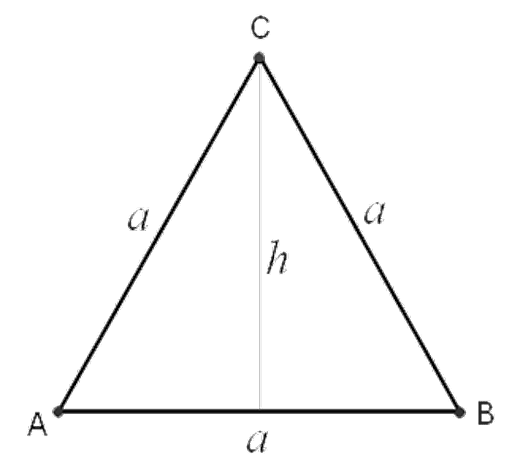
equilateral triangle

As shown in the diagram, Δ ABC is an equilateral triangle with sides of length a and an altitude of length h. This triangle will be used as reference for all the formulas of the equilateral triangle mentioned here.

Table of Content

Perimeter of an Equilateral Triangle
Semi-Perimeter of Equilateral Triangle
Altitude of Equilateral Triangle
Area of Equilateral
Things to Remember
Sample Questions

Key Takeaways: Equilateral Triangle, Area of Equilateral Triangle, Perimeter of Equilateral Triangle, Length of Altitude of Equilateral Triangle, Semi-perimeter of Equilateral Triangle

Perimeter of Equilateral Triangle

Perimeter of an Equilateral Triangle = sum of the length of all sides = a + a + a = 3a

Perimeter of an Equilateral Triangle = 3a

Angle Formula: Definition, Different Types, Solved Example	Triangles Important Questions: Important Similarity Concepts

Semi-Perimeter of an Equilateral Triangle

Semi-perimeter of an Equilateral Triangle

= \(\frac{\text{ Perimeter of an Equilateral Triangle}}{2} = \frac{3a}{2}\)

Altitude of Equilateral Triangle

Length of the altitude of an equilateral triangle = \(\frac{\sqrt{3}a}{2}\)

Altitude of Equilateral Triangle

Area of Equilateral Triangle

Area of a triangle A = \(\frac{1}{2}\)bh

For an equilateral triangle, b = a and h = \(\frac{\sqrt{3}a}{2}\)

So, the area of an equilateral triangle = \(\frac{1}{2}a \times \frac{\sqrt{3}a}{2} \times \frac{\sqrt{3}}{4} a^2\)

Area of an Equilateral Triangle = \(\frac{\sqrt{3}}{4}a^2\)

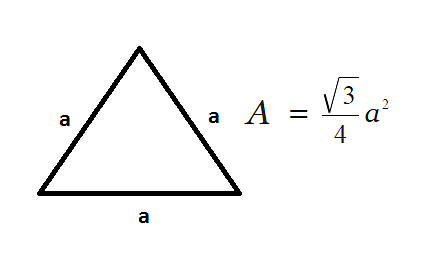
Types of Triangles: Important Terms, Scalene, Acute, and Obtuse Triangle	Properties of Triangle: Classification, Diagrams, Sample Questions
Area of a Triangle: Formula, Types and Solved Examples	Scalene Triangle: Definition, Area, Perimeter and Examples

Things To Remember

In an equilateral triangle, all sides and all angles are equal, and the measure of each internal angle is 60º.
Perimeter of an equilateral triangle = 3a
The semi-perimeter of an equilateral triangle is equal to half its perimeter.
Length of the altitude of an equilateral triangle = \(\frac{\sqrt{3}a}{2}\)
Area of an equilateral triangle =\(\frac{\sqrt{3}}{4}a^2\)

Sample Questions

Ques: The length of an equilateral triangle is 12 cm. Calculate its area, perimeter, semi-perimeter, and length of altitude. (5 marks)

Ans: a = 12 cm

Area

Area of an Equilateral Triangle = \(\frac{\sqrt{3}}{4}a^2\)

Area = \(\frac{\sqrt{3}}{4}(12)^2\)=\(\sqrt{3} \times12 \times 3\) = \(36 \sqrt{3}\) cm2

Perimeter

Perimeter of an Equilateral Triangle = 3a

Perimeter = 3 × 12 = 36 cm

Semi-perimeter

Semi-perimeter of an Equilateral Triangle =

= \(\frac{\text{ Perimeter of an Equilateral Triangle}}{2} = \frac{36}{2}\)= 18 cm

Altitude

Length of the altitude of an equilateral triangle = \(\frac{\sqrt{3}a}{2}\)

Altitude =\(\frac{\sqrt{3} \times 12}{2} = 6 \sqrt{3}\)

The area, perimeter, semi-perimeter, and length of the altitude of this triangle are \(36 \sqrt{3}\) cm2, 36 cm, 18 cm, and \( 6 \sqrt{3}\) cm, respectively.

Ques: If the perimeter of an equilateral triangle is 99 cm, then find the length of its sides. (3 marks)

Ans: Perimeter = 99 cm

Perimeter of an equilateral triangle = 3a

99 = 3a

a = 33 cm

So, the length of each side of this equilateral triangle is 33 cm.

Ques: Calculate the area of an equilateral triangular park whose each side measures 200 m. (3 marks)

Ans: a = 200 m

Area of an Equilateral Triangle = \(\frac{\sqrt{3}}{4}a^2\)

Area of triangular park = \(\frac{\sqrt{3}}{4}(200)^2\) = \(\sqrt{3} \times12 \times 3\) = \(10000 \sqrt{3}\) m²

So, the area of this equilateral triangular park is \(10000 \sqrt{3}\)m².

Ques: If the semi-perimeter of an equilateral triangle is 15 cm, then calculate its perimeter, area, and length of altitude. (5 marks)

Ans: semi-perimeter = 15 cm

Perimeter

Perimeter of equilateral triangle = 2 × semi-perimeter = 2 × 15 = 30 cm

Perimeter of equilateral triangle = 3a

30 = 3a

a = 10 cm

Area

Area of an Equilateral Triangle = \(\frac{\sqrt{3}}{4}a^2\)

Area = \(\frac{\sqrt{3}}{4}(10 )^2\) = \(\sqrt{3} \times5 \times 5\) = \(25 \sqrt{3}\) m²

Altitude

Length of the altitude of an equilateral triangle = \(\frac{\sqrt{3}}{4}a^2\)

Altitude= \(\frac{\sqrt{3} \times 10}{2} = 5 \sqrt{3}\)

The perimeter, area, and length of altitude of this equilateral triangle are 30 cm, \(25 \sqrt{3}\) cm2, and \(5 \sqrt{3}\) cm, respectively.

Ques: Calculate the area of an equilateral triangle whose perimeter is 45 cm. (3 marks)

Ans: perimeter = 45 cm

Perimeter of an equilateral triangle = 3a

45 = 3a

a = 15 cm

Area of an Equilateral Triangle = \(\frac{\sqrt{3}}{4}a^2\)

Ques: Calculate the semi-perimeter of an equilateral triangle with an altitude of 20 units. (4 marks)

Ans: h = 20 units

Length of the altitude of an equilateral triangle =\(\frac{\sqrt{3}a}{2}\)

Semi-perimeter of an Equilateral Triangle = \(\frac{\sqrt{3}a}{2}\)

Semi-perimeter =

So, the semi-perimeter of this triangle is \(20 \sqrt{3}\) units.

Ques: Calculate the area of a circumscribed circle of an equilateral triangle with a length of each side of 5 cm. (3 marks)

Ans: a = 5 cm

The formula for calculating the radius of a circumscribed circle of an equilateral triangle is given by r = \(\frac{\sqrt{3}a}{3}\)

Area of a circle,

So, the area of this circumscribed circle of an equilateral triangle is \(\frac{25 \pi}{3}\) cm2.

Area of Equilateral Triangle, Perimeter & Altitude Formulas

Perimeter of Equilateral Triangle

Semi-Perimeter of an Equilateral Triangle

Altitude of Equilateral Triangle

Area of Equilateral Triangle

Things To Remember

Sample Questions

CBSE X Related Questions

1.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

2.
Check whether \(6n\) can end with the digit \(0\) for any natural number \(n\).

6.
An umbrella has 8 ribs which are equally spaced (see Fig. 11.10). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

Comments

SUBSCRIBE TO OUR NEWS LETTER

Area of Equilateral Triangle, Perimeter & Altitude Formulas

Perimeter of Equilateral Triangle

Semi-Perimeter of an Equilateral Triangle

Altitude of Equilateral Triangle

Area of Equilateral Triangle

Things To Remember

Sample Questions

CBSE X Related Questions

1. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

2. Check whether \(6n\) can end with the digit \(0\) for any natural number \(n\).

6. An umbrella has 8 ribs which are equally spaced (see Fig. 11.10). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

Comments

SUBSCRIBE TO OUR NEWS LETTER

1.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

2.
Check whether \(6n\) can end with the digit \(0\) for any natural number \(n\).

6.
An umbrella has 8 ribs which are equally spaced (see Fig. 11.10). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.