
Arpita Srivastava Content Writer
Content Writer
Isosceles triangle is one in which the lengths of the two sides are equal. In this type of triangle, either two sides are of equal length, or at least two sides are of equal length. Isosceles triangle having at least two sides of equal length is considered a special equilateral triangle case.
- In an isosceles triangle, the two angles on the opposite sides of the same length are equal.
- It is a type of triangle with two congruent sides.
- It is classified into three types, namely acute, right angle and obtuse isosceles triangle.
- The two equal sides of the triangle are called legs.
- The third unequal side of the isosceles triangle is called the base.
- Angles formed between the legs of the triangle are called vertex angles.
- Golden Triangles and Catalan Solids are some examples of isosceles triangle.
Key Terms: Isosceles Triangle, Sides, Equilateral Triangle, Triangle, Obtuse Isosceles Triangle, Acute Isosceles Triangle, Right Isosceles Triangle, Congruent Sides
What is Isosceles triangle?
[Click Here for Sample Questions]
Isosceles triangle is a type of triangle that has two sides of equal length. In this type of triangle, angles opposite to two sides are equal. The name is derived from a Greek word named iso, which means same, and skelos, which means legs.
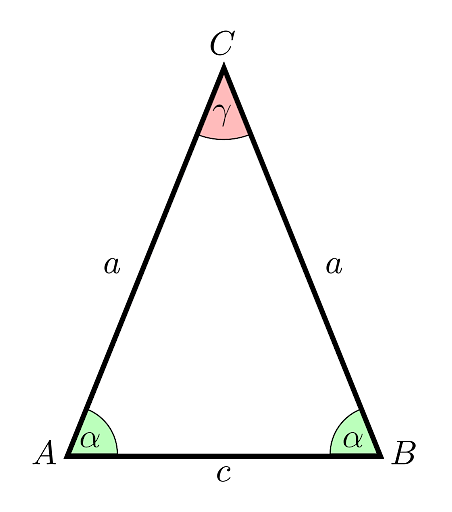
Isosceles Triangle
The above figure explains the concept of an isosceles triangle.
- If the sides AC and BC of a triangle ABC are equal, then ABC is an isosceles triangle with ∠ A = ∠B.
- "If the two sides of a triangle are congruent, then the angle opposite them is likewise congruent," says the theorem that characterises the isosceles triangle.
- The two equal sides are the legs, and the third is called the base.
- The vertex which is opposite to the base is called the apex.
- A base angle is a type of angle which is formed involving the third side of a triangle.
Read more:
Types of Isosceles Triangle
[Click Here for Sample Questions]
In general, the isosceles triangle may be divided into three types:
Isosceles Acute Triangle
Isosceles Acute Triangle is a type of triangle in which two angles opposing the legs are equal and smaller than 90 degrees. The two sides which are opposite to these angles are also equal. The perpendicular bisector of the base of every isosceles triangle has a symmetry axis.
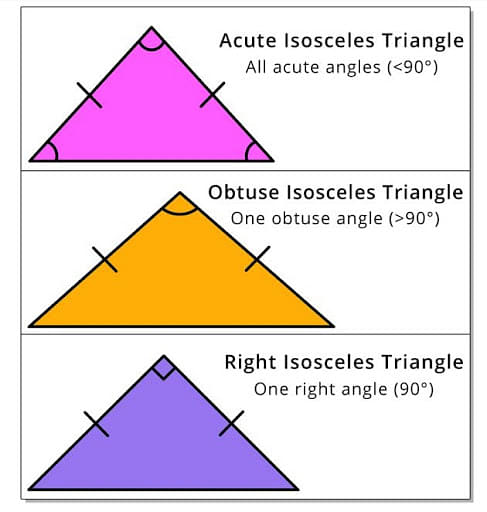
Types of Isosceles Triangle
Isosceles Right Triangle
Isosceles Right Triangle has two equal sides, one of which serves as the perpendicular and the other as the triangle's base. The hypotenuse is the third unequal side of the triangle. As a result, we may use Pythagoras theorem, which states that the square of the hypotenuse equals the sum of the squares of the base and perpendicular.
- Assume the sides of the right isosceles triangle are a, a, and h, with a representing the two equal sides and h representing the hypotenuse.
- h = √(a² + a²) = √2a² = a√2
- or h = \(\sqrt{2a}\)

Isosceles right triangle
Isosceles Obtuse Triangle
Isosceles Obtuse Triangle is defined as a triangle with one of its angles larger than 90 degrees (right angle). A triangle with more than two obtuse angles is also impossible to draw. The obtuse triangle can be a scalene triangle or an isosceles triangle, as we know. As a result, an isosceles obtuse triangle is one with two equal sides and an obtuse angle.

Obtuse Isosceles Triangle
Read more: Circumference of Circle
Angles of Isosceles Triangle
[Click Here for Sample Questions]
Two of the isosceles triangle's three angles are equal in measure, which is the polar opposite of the equal sides. As a result, one of the angles needs to be more balanced. If we are given the measure of an unequal angle, we can calculate the other two angles using the angle sum property.
- The angles which are different from apex angles are equal in value.
- The sum of three interior angles is equivalent to 180 degrees.

Isosceles Triangle
Solved Example of Angles of Isosceles TriangleExample: Let the measure of the unequal angle is 70° and the other two equal angles measures x, then as per angle sum rule, 70° + x + x = 180° 70° + 2x = 180° 2x = 180 – 70 = 110° x = 110/2 = 55° Hence, the measure of the other two angles of an isosceles triangle is 55°. |
Read more: Area of Segment of a Circle
Properties of Isosceles Triangle
[Click Here for Sample Questions]
Some important propertoes of isosceles triangle are as follows:
- As the two sides of this triangle are equal, the uneven side is referred to as the triangle's base.
- The angles opposing the triangle's two equal sides are always equal.
- From the midpoint of the base to the vertex (topmost) of an isosceles triangle, the height is measured.
- The third angle of a right isosceles triangle is 90 degrees.
Read more: Quadrilateral Angle Sum Property
Isosceles Triangle Theorem
[Click Here for Sample Questions]
According to the isosceles triangle theorem, if two sides are congruent, then the angles opposite to the two sides are also congruent. Alternatively, if two angles are congruent in an isosceles triangle, the sides opposite are also congruent.
- In the below triangle ABC,
- AB = BC
- ∠ABC = ∠ACB

Isosceles Triangle Theorem
Read more: Perimeter of a parallelogram
Isosceles Triangle Formulas
[Click Here for Sample Questions]
Isosceles triangle is a three-sided two-dimensional shape. The area and perimeter are used to calculate the isosceles triangle. Let's take a closer look at the isosceles triangle's area and perimeter.
Area of Isosceles triangle
The region inhabited by an isosceles triangle in two-dimensional space is defined as its area. In general, the base and height of an isosceles triangle are half the product of the base and height. The area of an isosceles triangle may be calculated using the following formula:
The area of an isosceles triangle is given by,
A = ½ × b × h Square units
Where,
b → Triangle's base
h → Height
Solved Example of Area of Isosceles TriangleGiven below are the example of area of isosceles triangle. Example: Find the area of an isosceles acute triangle if the base is 12 units and the height is 10 units. Solution: Given, base (b) = 12 units and height (h) = 10 units. The formula to calculate the area is 1/2 × b × h square units. By substituting the values, we get area = 1/2 × 12 × 10. ⇒ Area = 6 × 10 = 60 Therefore, the area of the given isosceles acute triangle is 60 square units. |
Read more: Area of a Trapezoid Formula
Perimeter of the Isosceles triangle
The perimeter of any form, as we all know, is the shape's boundaries. Similarly, the perimeter of an isosceles triangle is equal to the total of the triangle's three sides. If we know the base and side of an isosceles triangle, we can calculate its perimeter. The perimeter of an isosceles is given by the formula,
P = 2a + b
Where,
a → Length of the two equal legs of an isosceles triangle
b → Base of the triangle.
Solved Example of Perimeter of Isosceles TriangleGiven below are the example of perimeter of isosceles triangle. Example: Find the perimeter of an isosceles triangle, if the base is 20 inches and the equal sides are 36 inches each. Solution: We know that formula of the perimeter of an isosceles triangle (p) = 2a + b, where a is the length of each of the equal sides. Substituting the values in the perimeter of an isosceles triangle formula, we get, P = 2(36) + 20 = 92 inches. |
Read more: Properties of a Parallelogram
Isosceles Triangle Altitude
The vertex angle is bisected when an altitude is drawn to the base of the isosceles triangle. The two congruent triangles are formed as it bisects the base. The triangle's altitude creates the necessary right angle, and the altitude becomes the shared legs. A triangle's congruent legs also form the congruent hypotenuse. As a result, the height bisects the base.

Altitude of the isosceles triangle
Solved Example of Isosceles Triangle AltitudeGiven below are the example of isosceles triangle altitude. Example: The area of a triangle is 36 square units. Find the length of the altitude if the length of the base is 9 units. Solution: We know that altitude of a triangle, h = (2 × Area) / Base. |
Read More: Angles of a Parallelogram
Things to Remember
- Isosceles triangle consists of two equal sides and two equal angles.
- In addition, the two angles on the opposite sides of the two equal sides are also equal.
- If the two angles are smaller than 90 degrees, the isosceles triangle is called an acute isosceles triangle.
- The obtuse triangle is defined as a triangle with one of its angles larger than 90 degrees.
- Two of the isosceles triangle's three angles are equal in measure, which is the polar opposite of the equal sides.
- The area of an isosceles triangle is given by A = ½ × b × h Square units
- Perimeter of an isosceles is given by the formula P = 2a + b.
- The vertex angle is bisected when an altitude is drawn to the isosceles triangle's base.
Read More:
Sample Questions
Ques. Define an isosceles triangle? (2 marks)
Ans. A triangle with two equal sides is called an isosceles triangle. In addition, the angles on the opposite sides of the two equal sides are congruent. The two equal sides are the legs, and the third is called the base. The vertex which is opposite to the base is called the apex. A base angle is a type of angle which is formed involving the third side of a triangle.
Ques. Mention the several isosceles triangle categories? (3 marks)
Ans. The isosceles triangle is categorized as follows based on the angles between the two legs of a triangle:
- Isosceles acute triangle: Isosceles Acute Triangle is a type of triangle in which two angles opposing the legs are equal and smaller than 90 degrees.
- Isosceles right triangle: Isosceles Right Triangle has two equal sides, one of which serves as the perpendicular and the other as the triangle's base.
- Isosceles obtuse triangle: Isosceles Obtuse Triangle is defined as a triangle with one of its angles larger than 90 degrees (right angle).
Ques. What is the isosceles triangle's area and perimeter? (2 marks)
Ans. The area of an isosceles triangle is half the product of the triangle's base and height. The area of an isosceles triangle is calculated using ½ × b × h Square units
The perimeter of an isosceles triangle is calculated using the formula 2a+b units, where "a" is the length of two equal legs and "b" is the base of the isosceles triangle.
Ques. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at 0. Join A to 0. Show that (3 marks) (i) OB = OC (ii) AO bisects ∠A
Ans. i) in ΔABC, we have
AB = AC [Given]
∴ ∠ABC = ∠ACB [Angles opposite to equal sides of A are equal]

⇒ 1/2∠ABC = 1/2∠ACB
or ∠OBC = ∠OCB
⇒ OC = OB [Sides opposite to equal angles of a Δ are equal]
(ii) In ΔABO and ΔACO, we have
AB = AC [Given]
∠OBA = ∠OCA [ ?1/2∠B = 1/2∠C]
OB = OC [Proved above]
ΔABO ≅ ΔACO [By SAS congruency]
⇒ ∠OAB = ∠OAC [By C.P.C.T.]
⇒ AO bisects ∠A.
Ques. In ΔABC, AD is the perpendicular bisector of BC (see figure). Show that Δ ABC is an isosceles triangle in which AB = AC? (2 marks)

Ans. Since AD is the bisector of BC.
∴ BD = CD
Now, in ΔABD and ΔACD, we have
AD = DA [Common]
∠ADB = ∠ADC [Each 90°]
BD = CD [Proved above]
∴ ΔABD ≅ ΔACD [By SAS congruency]
⇒ AB = AC [By C.P.C.T.]
Thus, ΔABC is an isosceles triangle.
Ques. In ΔABC, AD is the perpendicular bisector of BC (see figure). Show that ΔABC is an isosceles triangle in which AB = AC? (2 marks)

Ans. Since AD is the bisector of BC.
∴ BD = CD
Now, in ΔABD and ΔACD, we have
AD = DA [Common]
∠ADB = ∠ADC [Each 90°]
BD = CD [Proved above]
∴ ΔABD ≅ ΔACD [By SAS congruency]
⇒ AB = AC [By C.P.C.T.]
Thus, ΔABC is an isosceles triangle.
Ques. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see figure). Show that these altitudes are equal? (2 marks)

Ans.
ΔABC is an isosceles triangle
∴ AB = AC
⇒ ∠ACB = ∠ABC [Angles opposite to equal sides of a A are equal]
⇒ ∠BCE = ∠CBF
Now, in ΔBEC and ΔCFB
∠BCE = ∠CBF [Proved above]
∠BEC = ∠CFB [Each 90°]
BC = CB [Common]
∴ ΔBEC ≅ ΔCFB [By AAS congruency]
So, BE = CF [By C.P.C.T.]
Ques. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure)? (2 marks)

Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC i.e., ABC is an isosceles triangle.
Ans.
(i) In ΔABE and ΔACE, we have
∠AEB = ∠AFC
[Each 90° as BE ⊥ AC and CF ⊥ AB]
∠A = ∠A [Common]
BE = CF [Given]
∴ ΔABE ≅ ΔACF [By AAS congruency]
(ii) Since, ΔABE ≅ ΔACF
∴ AB = AC [By C.P.C.T.]
⇒ ABC is an isosceles triangle.
Ques. ABC and DBC are isosceles triangles on the same base BC (see figure). Show that ∠ ABD = ∠ACD? (3 marks)

Ans.
In ΔABC, we have
AB = AC [ABC is an isosceles triangle]
∴ ∠ABC = ∠ACB …(1)
[Angles opposite to equal sides of a Δ are equal]
Again, in ΔBDC, we have
BD = CD [BDC is an isosceles triangle]
∴ ∠CBD = ∠BCD …(2)
[Angles opposite to equal sides of a A are equal]
Adding (1) and (2), we have
∠ABC + ∠CBD = ∠ACB + ∠BCD
⇒ ∠ABD = ∠ACD
Ques. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠BCD is a right angle? (5 marks)
Ans. AB = AC [Given] …(1)
AB = AD [Given] …(2)
From (1) and (2), we have
AC = AD
Now, in ΔABC, we have
∠ABC + ∠ACB + ∠BAC = 180° [Angle sum property of a A]
⇒ 2∠ACB + ∠BAC = 180° …(3)
[∠ABC = ∠ACB (Angles opposite to equal sides of A are equal)]
Similarly, in ΔACD,
∠ADC + ∠ACD + ∠CAD = 180°
⇒ 2∠ACD + ∠CAD = 180° …(4)
[∠ADC = ∠ACD (Angles opposite to equal sides of a A are equal)]
Adding (3) and (4), we have
2∠ACB + ∠BAC + 2 ∠ACD + ∠CAD = 180° +180°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2∠BCD +180° = 360° [∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360° – 180° = 180°
⇒ ∠BCD = 180°/2 = 90°
Thus, ∠BCD = 90°
Ques. Find the perimeter of an isosceles triangle, if the base is 20 inches and the equal sides are 16 inches each? (2 marks)
Ans. We know that formula of the perimeter of an isosceles triangle (p) = 2a + b, where a is the length of each of the equal sides.
Here, a = 16 inches and b = 24 inches.
Substituting the values in the perimeter of an isosceles triangle formula, we get, P = 2(16) + 20 = 52 inches.
Ques. Find the area of an isosceles acute triangle if the base is 11 units and the height is 11 units? (2 marks)
Solution: Given, base (b) = 11 units and height (h) = 11 units. The formula to calculate the area is 1/2 × b × h square units. By substituting the values, we get area = 1/2 × 11 × 11.
⇒ Area = 60.5
Therefore, the area of the given isosceles acute triangle is 60.5 square units.
Ques. The area of a triangle is 56 square units. Find the length of the altitude if the length of the base is 7 units? (3 marks)
Ans. We know that altitude of a triangle, h = (2 × Area) / Base.
Given, area = 56 square units and base = 7 units.
Altitude 'h' = (2 × 56) / 9
= 112/7
= 16 units.
Therefore, altitude 'h' = 16 units.
Ques. Calculate the length of the altitude of a scalene triangle whose sides are 7 units, 5 units, and 4 units respectively? (3 marks)
Ans. The perimeter of a triangle is the sum of all the sides = 7 + 5 + 4 = 14 units. Semi-perimeter (s) = 16/2 =8 units. Let us name the sides of the scalene triangle to be 'a', 'b', and 'c' respectively. Therefore, a = 7 units, b = 4 units and c = 5 units;
The altitude of the triangle:
h=2√s(s−a)(s−b)(s−c)/ b
Altitude(h) = 2√12(8-7)(8-5)(8-4)/4
Altitude(h) = 2√12 ×1 ×3 ×4 /4
Altitude (h) = 6 units
Ques. The area of a triangle is 100 square units. Find the length of the altitude if the length of the base is 10 units? (3 marks)
Ans. We know that altitude of a triangle, h = (2 × Area) / Base.
Given, area = 100 square units and base = 10 units.
Altitude 'h' = (2 × 100) / 10
= 200/10
= 20 units.
Therefore, altitude 'h' = 20 units.
Read Also:






Comments