Area of Parallelogram: How to Calculate Area of Parallelogram?

Content Writer

Area of Parallelogram is the region or space occupied by a parallelogram in a two-dimensional plane. It is the space enclosed with the four sides of a parallelogram.

Parallelogram is a type of quadrilateral formed by parallel lines.
It is a closed polygon whose opposite sides are equal and parallel.
Parallelogram is divided into there major types namely Square, Rectangle, and Rhombus.

Area of Parallelogram is the product of its base and height. Area of Parallelogram is calculated using the formula:

Area of Parallelogram = Base x Height

Table of Content

What is Parallelogram?
Area of Parallelogram
Area of Parallelogram Formula
How to Calculate Area of Parallelogram?
Area of Parallelogram in Vector Form
Things to Remember
Sample Questions

Key Terms: Parallelogram, Area of Parallelogram, Area of Parallelogram Formula, Length, Diagonal, Quadrilateral, Base, Height

What is Parallelogram?

[Click Here for Sample Questions]

Parallelogram is a special type of quadrilateral entirely formed by parallel lines. A quadrilateral is said to be a parallelogram if its opposite sides are parallel and congruent.

Parallelogram is a quadrilateral in which both pairs of opposite sides are parallel and equal.
It has two intersecting and non-equal diagonals.
The diagonals of a parallelogram bisect each other and divide it into two congruent triangles.
Since the opposite sides are equal, the opposite angles of a parallelogram are also equal.
Rectangle, Square, and Rhombus are the three types of Parallelograms in Geometry.

Parallelogram

Area of Parallelogram

[Click Here for Sample Questions]

Area of Parallelogram is the region occupied within the four sides of a Parallelogram in a two-dimensional plane.

It is the number of square units that can fit within the parallelogram.
Area of Parallelogram is equal to the product of its base and height.
It is measured in square units such as square meters (m²), square cm (cm²), square feet (ft²), etc.

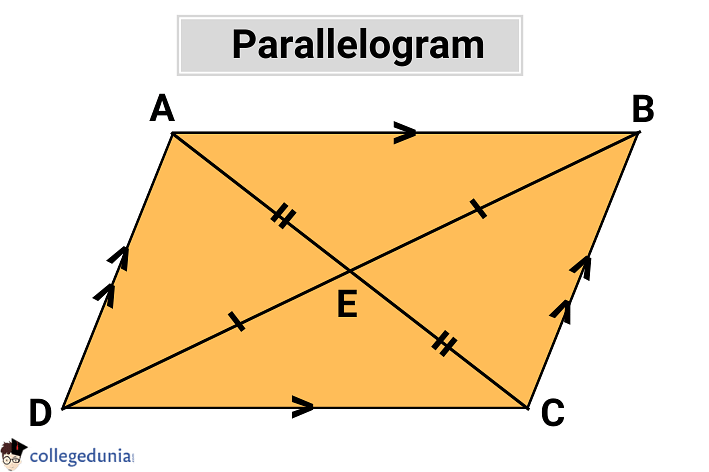
Area of Parallelogram

Area of a Parallelogram

In the given figure, the area of the parallelogram ABCD is the area occupied within its four sides.

Read More:

Relevant Concepts
Parallelogram Formula	Perimeter of a Parallelogram	Properties of a Parallelogram
Difference between Rhombus and Parallelogram	Trapezoids	Areas of Parallelograms and Triangles

Area of Parallelogram Formula

[Click Here for Sample Questions]

Area of Parallelogram is the product of the base and height of the parallelogram. The base and altitude of a parallelogram are perpendicular to each other. Area of Parallelogram Formula is given as follows:

Area of Parallelogram = b x h

Where

b: Base of Parallelogram
h: Height of Parallelogram

Solved Example

Example: What will be the area of a sheet in the shape of a parallelogram, if its base is 20 cm, and its height is 8 cm?

Solution: Given that

Base of Parallelogram (b) = 20 cm
Height of Parallelogram (h) = 8 cm

Using the Area of Parallelogram Formula

Area of Parallelogram = b x h

Area of Sheet = b × h = (20) × (8) = 160 cm²

Thus, the area of the sheet is 160 in².

How to Calculate Area of Parallelogram?

[Click Here for Sample Questions]

Area of Parallelogram can be calculated easily using its base and height. Area of Parallelogram can also be calculated if its two diagonals are given along with any of their intersecting angles. It can also be calculated if the length of the parallel sides is known, along with any of the angles between the sides.

Thus, there are three different ways to calculate the Area of Parallelogram:

Using Base and Height
Using Diagonals and their Intersecting Angle
Using Length of Parallel Sides and Angle between them.

All three methods are explained in detail below.

Area of Parallelogram Using Base and Height

Area of Parallelogram is usually calculated by multiplying the base and height of the parallelogram. It is calculated using the given formula:

Area of Parallelogram = b x h

Here, be refers to the Base of the Parallelogram while h refers to the Height of the Parallelogram.

Solved Example

Example: Calculate the area of a parallelogram with the base as 5 cm and height as 3 cm.

Solution: Given that,

Base of Parallelogram = 5 cm
Height of Parallelogram = 3 cm

Using the Area of Parallelogram Formula

Area of Parallelogram = b x h

Area of Parallelogram = b × h = 5 × 3 = 15 cm²

Thus, the area of the given parallelogram is 15 cm².

Area of Parallelogram Using Diagonals and Intersecting Angle

There are two diagonals of a parallelogram that bisect each other and divide the parallelogram into two congruent triangles. Area of Parallelogram can also be calculated using the two diagonals and their intersecting angle. It is calculated using the given formula:

Area of Parallelogram = 1/2 x d₁ x d₂ sin(x)

Where

d₁: First Diagonal of Parallelogram
d₂: Second Diagonal of Parallelogram
y: Angle between Two Diagonals

Solved Example

Example: Calculate the area of a parallelogram with the length of diagonals as 15.6 cm and 17.2 cm respectively. The angle of the intersection of the two diagonals is 120^o.

Solution: Given that

Length of First Diagonal = 15.6 cm
Length of Second Diagonal = 17.2 cm

Using the Area of Parallelogram Formula,

Area = 1/2 × d₁ × d₂ sin (x)

Area of Parallelogram = ½ x 15.6 x 17.2 sin(120)

= ½ x 15.6 x 17.2 x √3/2

= 232.37 cm²

Thus, the area of the given parallelogram is 232.37 cm².

Area of Parallelogram Using Lengths of Sides

Area of Parallelogram can also be calculated using the length of the parallel sides and the angle between them. In this method, the concept of trigonometry is used to find the area. It is calculated using the formula:

Area of Parallelogram = ab sin(x)

Where

a: First Side of Parallelogram
b: Second Side of Parallelogram
x: Angle between Sides a and b.

Solved Example

Ques. If the angle between the two sides of a parallelogram is 90^o and the length of the two parallel sides are 4 cm and 3 cm respectively, calculate the area of the parallelogram.

Solution: Given that,

Length of First Side = 4 cm
Length of Second Side = 3 cm
Angle between Both Sides = 90^o

Using the Area of Parallelogram Formula,

Area of Parallelogram = ab sin(x)

Area of Parallelogram = 3 x 4 x sin (90)

= 12 sin(90) = 12 x 1 (sin 90^o= 1)

= 12 cm²

Thus, the area of the given parallelogram is 12 cm².

Area of Parallelogram in Vector Form

[Click Here for Sample Questions]

Area of Parallelogram can also be calculated with the help of its diagonals when the sides of a parallelogram are represented in vector form. Considering there are two sides as vector a and vector b of a parallelogram then the resulting vector is the diagonal of a parallelogram. Area of Parallelogram in vector form using the adjacent sides is given using the formula:

Area of Parallelogram = | \(\vec{a}\times\vec{b}\)|

Here \(\vec{a}\) and \(\vec{b}\) are the vectors representing two adjacent sides of the parallelogram.

In order to find the area of a parallelogram with respect to diagonals, suppose d₁ and d₂arein vector form. Then,

\(\vec{a} + \vec{b} = \vec{d_1}\)

\(\vec{b} + (\vec{-a}) = \vec{d_2}\)

\(\vec{b} - \vec{a} = \vec{d_2}\)

\(\Rightarrow\) \(\vec{d_1} * \vec{d_2} = (\vec{a} + \vec{b})(\vec{b} - \vec{a})\)

= \(\vec{a} * (\vec{b} - \vec{a}) + \vec{b} * (\vec{b} - \vec{a})\)

= \(\vec{a} * \vec{b} - \vec{a} * \vec{a} + \vec{b}* \vec{b} - \vec{b} * \vec{a}\)

Since\(\vec{a} * \vec{a} = 0\) and \(\vec{b} * \vec{b} = 0\)

\(\Rightarrow\) \(\vec{a} * \vec{b} = \vec{-b} * \vec{a}\)

Since \(\vec{a} * \vec{b} = \vec{-b} * \vec{a}\)

\(\vec{d_1} + \vec{d_2} = \vec{a} * \vec{b} - (-(\vec{a} * \vec{b}))\)

= \(2(\vec{a} * \vec{b})\)

Therefore, when diagonals are given in a vector form the area of a parallelogram can be stated as

Area of Parallelogram = \(\frac{1}{2}|(\vec{d_1} * \vec{d_2})|\)

Where, \(\vec{d_1}\)and \(\vec{d_2}\)are the diagonals of the parallelogram.

Check More:

Related Topics
Area of a Triangle	Area of Polygon	Area of General Quadrilateral
Area of Rectangle	Area of Isosceles Triangle	Area of Segment of a Circle

Things to Remember

Paralleogram is a quadrilateral whose opposite sides are equal and parallel.
Area of Parallelogram is the region occupied by a parallelogram within its four sides.
It is the product of the base and height of the parallelogram.
Area of Parallelogram = Base x Height
Area of Parallelogram with Diagonals and Intersecting Angle is given as 1/2 x d₁ x d₂ sin(y).
Area of Parallelogram with Length of Sides is given as ab sin(x).
Area of Parallelogram in Vector Form is | \(\vec{a}\times\vec{b}\)|.

For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates

Sample Questions

Ques. The area of a playground that is in the shape of a parallelogram is 2500 in²and one of its sides is 250 m. Find out the corresponding altitude using the Area of Parallelogram Formula. (3 Marks)

Ans. Given that,

Area of Playground = 2500 in²
Sides of Playground = 250 in

Using Area of Parallelogram Formula,

Area of Parallelogram = Base x Height

Height = Area of Parallelogram/Base = 2500/250 = 10 in.

Therefore, the corresponding altitude of the playground is 10 in.

Ques. What are the different types of a Parallelogram? (3 Marks)

Ans. The different types of a parallelogram are as follows:

Rectangle: Rectangle is a parallelogram that has two pairs of equal and parallel opposite sides and four right angles.
Rhombus: Rhombus is a parallelogram that has four equal sides in which the opposite angles are equal.
Square: Square is a parallelogram that has four equal sides and four right angles.

Ques. What is the formula for Area of Parallelogram? (3 Marks)

Ans. There are three methods to calculate the Area of a Parallelogram. These are as follows:

Area of Parallelogram = b x h
Area of Parallelogram = 1/2 x d₁ x d₂ sin(y)
Area of Parallelogram = ab sin(x)

Where

b = Base of the Parallelogram
h = Height of the Parallelogram
d₁ = First Diagonal of the Parallelogram
d₂ = Second Diagonal of the Parallelogram
y = Angle between the Diagonals
a = First Side of the Parallelogram
b = Second Side of the Parallelogram
x = Angle between the Sides ‘a’ and ‘b’

Ques. What will be the area of a parallelogram if its base and height are 4 cm and 8 cm respectively? (3 Marks)

Ans. Given that,

Base of Parallelogram = 4 cm
Height of Parallelogram = 8 cm

Using the Area of Parallelogram Formula

Area of Parallelogram = b x h

Area of Parallelogram = b × h = 4 × 8 = 32 cm²

Thus, the area of the given parallelogram is 32 cm².

Ques. Find the area of the parallelogram if the length of its adjacent sides is 20 cm and 25 cm and the measure of the angle between the adjacent sides is 34°. (3 Marks)

Ans. Given that,

Length of First Side = 20 cm
Length of Second Side = 25 cm
Angle between Both Sides = 34^o

Using the Area of Parallelogram Formula,

Area of Parallelogram = ab sin(x)

Area of Parallelogram = 20 x 25 x sin(34°)

= 500 x 0.55919

= 279.595 cm²

Thus, the area of the given parallelogram is 279.595 cm².

Ques. Find the height and base of a parallelogram when the area of a parallelogram is 500 sq. cm and its height is twice its base. (3 Marks)

Ans. Given that,

Area of Parallelogram = 500 cm²
Height, h = 2 x Base = 2b

Using the Area of Parallelogram Formula

Area of Parallelogram = b x h

500 = b x 2b

2b² = 500

b² = 250

b = 15.8 cm

Height, h = 2 x b = 31.6 cm.

Therefore, the height of the parallelogram is 31.6 cm.

Ques. Find the base and height of a parallelogram when the base is thrice its height and the area is 192 cm². (3 Marks)

Ans. Given that,

Area of Parallelogram = 192 cm²
Base, b = 3 x Height = 3h

Using the Area of Parallelogram Formula

Area of Parallelogram = b x h

192 = 3h x h

3 x h² = 192

h² = 64 = 8 cm

Since height is 8 cm, therefore base = 3 x h = 3 x 8 = 24 cm.

Thus, the base and height of the parallelogram are 24 cm and 8 cm respectively.

Ques. Find the area of a parallelogram when two parallel lines are 80 cm and 40 cm respectively and the angle between them is 56^o. (3 Marks)

Ans. Given that,

Length of First Side = 80 cm
Length of Second Side = 40 cm
Angle between Both Sides = 56^o

Using the Area of Parallelogram Formula,

Area of Parallelogram = ab sin(x)

Area of Parallelogram = 80 x 40 x sin(56°)

= 3200 sin(56°) = 2652.9 cm²

Thus, the area of the parallelogram is 2652.9 cm².

Ques. Calculate the area of a parallelogram whose diagonals are 18 cm and 15 cm, and the angle of the intersection is 43^o between the diagonals. (3 Marks)

Ans. Given that,

Length of First Diagonal = 18 cm
Length of Second Diagonal = 15 cm
Angle of Intersection = 43^o

Using the Area of Parallelogram Formula,

Area = 1/2 × d₁ × d₂ sin (x)

Area of Parallelogram = ½ x 18 x 15 sin(43^o)

= 135 sin(43^o) = 92.07 cm²

Thus, the area of the given parallelogram is 92.07 cm².

Ques. A parallelogram with two parallel sides of 30 cm and 40 cm with an angle between the two sides as 36^o. If the base of the parallelogram is 40 cm, find the height. (3 Marks)

Ans. Given that,

Length of First Side = 30 cm
Length of Second Side = 40 cm
Angle between Both Sides = 36^o
Base of Parallelogram = 40 cm

Using the Area of Parallelogram Formula,

Area of Parallelogram = ab sin(x)

Area of Parallelogram = 30 x 40 x sin(36°)

It is also known as the Area of Parallelogram is also equal to Base x Height. Thus,

30 x 40 x sin(36°) = 40 x H

1200 sin(36°) = 40 x H

Dividing both sides by 40,

H = (1200/40) sin(36°)

H = 30 sin(36°) = 17.63 cm

Therefore, the height of the parallelogram is 17.63 cm.

Check More:

Class 9 & 10 Study Guides
NCERT Solutions for Class 10 Science	NCERT Solutions for Class 9 Science	NCERT Solutions for Class 9 Maths
NCERT Solutions for Class 10 Maths	Biology MCQs	Chemistry Study Notes
Topics for Comparison in Physics	NCERT Solutions for Class 6 to 12	Important Chemistry Formulas
SI units in Physics	Topics with relation in physics	Class 12 Physics Practicals
Important Derivations in Physics	NCERT Solutions Class 6 to 12	Formulas in Physics
Physics MCQs	Comparison Topics in Biology	Comparison topics in Chemistry
Biology Study Notes	Chemistry MCQs	Maths MCQs
Math Study Material	Physics Study Notes	Important Maths Formulas

Area of Parallelogram: How to Calculate Area of Parallelogram?

What is Parallelogram?

Area of Parallelogram

Area of Parallelogram Formula

Solved Example

How to Calculate Area of Parallelogram?

Area of Parallelogram Using Base and Height

Solved Example

Area of Parallelogram Using Diagonals and Intersecting Angle

Solved Example

Area of Parallelogram Using Lengths of Sides

Solved Example

Area of Parallelogram in Vector Form

Things to Remember

Sample Questions

CBSE X Related Questions

1.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

2.
Check whether \(6n\) can end with the digit \(0\) for any natural number \(n\).

3.
If 3 cot A = 4, check whether \(\frac{(1-\text{tan}^2 A)}{(1+\text{tan}^2 A)}\) = cos² A – sin²A or not

6.
Find the sums given below :
\(7 + 10\frac 12+ 14 + ....... + 84\)
\(34 + 32 + 30 + ....... + 10\)
\(–5 + (–8) + (–11) + ....... + (–230)\)

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

Area of Parallelogram: How to Calculate Area of Parallelogram?

What is Parallelogram?

Area of Parallelogram

Area of Parallelogram Formula

Solved Example

How to Calculate Area of Parallelogram?

Area of Parallelogram Using Base and Height

Solved Example

Area of Parallelogram Using Diagonals and Intersecting Angle

Solved Example

Area of Parallelogram Using Lengths of Sides

Solved Example

Area of Parallelogram in Vector Form

Things to Remember

Sample Questions

CBSE X Related Questions

1. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

2. Check whether \(6n\) can end with the digit \(0\) for any natural number \(n\).

3. If 3 cot A = 4, check whether \(\frac{(1-\text{tan}^2 A)}{(1+\text{tan}^2 A)}\) = cos2 A – sin2 A or not

6. Find the sums given below :\(7 + 10\frac 12+ 14 + ....... + 84\)\(34 + 32 + 30 + ....... + 10\)\(–5 + (–8) + (–11) + ....... + (–230)\)

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

1.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

2.
Check whether \(6n\) can end with the digit \(0\) for any natural number \(n\).

3.
If 3 cot A = 4, check whether \(\frac{(1-\text{tan}^2 A)}{(1+\text{tan}^2 A)}\) = cos² A – sin²A or not

6.
Find the sums given below :
\(7 + 10\frac 12+ 14 + ....... + 84\)
\(34 + 32 + 30 + ....... + 10\)
\(–5 + (–8) + (–11) + ....... + (–230)\)