
Arpita Srivastava Content Writer
Content Writer
The properties of the triangles are basically used to study the triangle and help us identify a triangle from a given set of data. It includes a sum of all three angles being 180°, the opposite side to the largest angle of the triangle being the greatest side, the exterior angle being equal to the sum of its interior contrary angles, etc.
- A triangle is a figure that has three sides, three vertices, and three angles.
- If you would take the sum of all the three angles of any triangle, it would equal 180° degrees.
- This is called the sum of all angles of a triangle.
- To study about the properties of a triangle, first study about the different triangles.
Read More: Rationalize the Denominator
| Table of Content |
Key Terms: Properties of a Traiangle, Equilateral Triangle, Isosceles Triangle, Scalene Triangle, Right Angle Triangle, Acute Angle Triangle
Types of Triangles
[Click Here for Sample Questions]
Triangles are divided into two categories, namely triangles based on side and triangles based on the angles. Equilateral Triangle, Isosceles Triangle and Scalene Triangle are triangles divided on the bases of each side. Right Angle Triangle, Acute Angle Triangle and Obtuse Angle Triangle are triangles divided on the basis of angles.
Equilateral Triangle
Equilateral is formed with the aid of the combination of words, i.e., “Equi” that means identical and “Lateral” which means facets. An equilateral triangle is also called a regular polygon or normal triangle when you consider that all its sides and angles are identical.
- Triangle having all three similar sides is known as an equilateral triangle.
- As all the three sides are the same, therefore the three respective angles are also the same.
- Hence each angle is 60°.

Equilateral Triangle
Read More: Angle FormulaIsosceles Triangle
A triangle having two sides of the same length while the length of the third side is different is known as an isosceles triangle. In this, the angle which is opposite to the two equal sides is always measured to be the same.
- Suppose in a triangle ∆ABC, if facets AB and AC are identical.
- Then ∆ABC is an isosceles triangle wherein ∠ B = ∠ C.
- The theorem that describes the isosceles triangle is “if the 2 facets of a triangle are congruent, then the angle contrary to them also are congruent”.
Read More: Congruence of Triangles: Rules & Solved Examples

Isosceles Triangle
Read More: Angle Between Two LinesScalene Triangle
Scalene triangle is a triangle having all three dissimilar sides. As all three sides are of different lengths, the angles also differ.
- However, the exclusive measurements don't affect the sum of all of the indoor angles of the scalene triangle.
- The sum of the 3 interior angles continually adds as much as 180° which satisfies the attitude sum assets of the triangle.
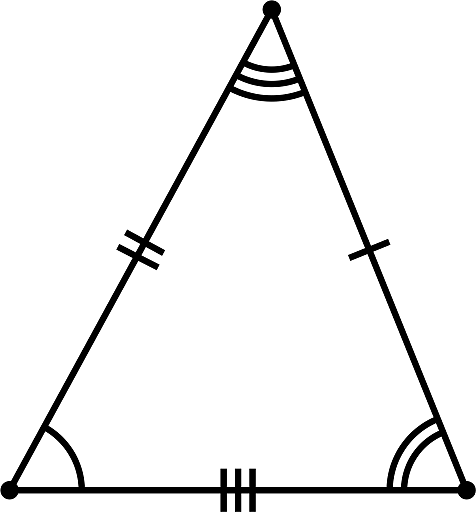
Scalene Triangle
Read More: Trigonometric IdentitiesRight Angle Triangle
Right Angle Triangle is a triangle having one of the three angles exactly 90°. The other two angles of a right-angle triangle are acute angles. In the right-angle triangle has a hypotenuse which is the largest side and is always opposite to the right angle.

Right Angle Triangle
Read More: Quadrilateral Angle Sum PropertyAcute Angle Triangle
An acute angle triangle is a triangle having all three angles less than 90° each. Therefore all the angles of an acute angle triangle are called acute angles. The examples of acute angle degrees are 63°, 31°, forty four°, sixty eight°, eighty three°, eighty five°. Hence, the acute angle degree lies in the ranges from zero° to less than ninety°
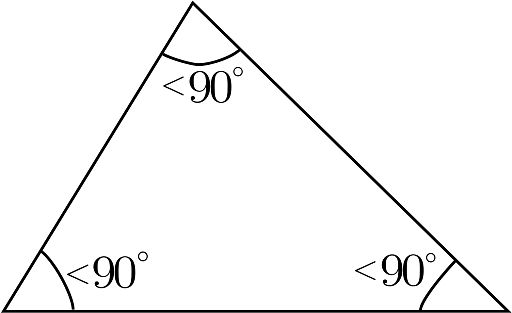
Acute Angle Triangle
Read More: Area of a TriangleObtuse/Oblique Angle Triangle
Obtuse Angle Triangle is a triangle that has one angle which is always more than 90°. A triangle cannot be right-angled and obtuse angled at the identical time. Since a proper-angled triangle has one right angle, the opposite two angles are acute. Therefore, an obtuse-angled triangle can in no way have a right perspective; and vice versa. The aspect contrary to the obtuse perspective inside the triangle is the longest.

Obtuse/Oblique Angle Triangle
Properties of a Triangle
[Click Here for Sample Questions]
The various properties of a triangles are as follows:
- The sum of all three angles of a triangle is 180°.
- The sum of the lengths of any two aspects of a triangle is usually more than the length of the third side.
- An exterior angle of a triangle is equal to the sum of its interior opposite angles.
- The sum of all exterior angles of any triangle is equal to 360°.
- Two triangles are said to be similar if their corresponding sides and angles are equal.
- The perimeter of a triangle is equal to the sum of all three sides of a triangle.
Read More: Distance Formula and Derivation of Coordinate Geometry
Things to Remember
- The properties of a triangle help us study and identify a triangle in a closed figure.
- Similarly, the distinction among the lengths of any aspect of a triangle is usually less than the length of the third aspect.
- The aspect contrary to the smallest interior angle is the shortest side and vice versa.
- Similarly, the side opposite to the biggest interior angle is the longest facet and vice versa.
- In the case of a right-angled triangle, this aspect is known as the hypotenuse.
- The peak of a triangle is identical to the length of the perpendicular dropped from a vertex to its opposite aspect.
- This facet is taken into consideration by the base.
Sample Questions
Ques. What is the identifying feature of a right angle triangle? (2 Marks)
Ans. The one angle of a right angle triangle will always be measured to be 90°. Note that no angle in a right angle triangle would be more than 90° as it would interfere with the rules of a right angle triangle and hence would be called an obtuse triangle.
Ques. Which triangle has all the three sides dissimilar to each other? (2 Marks)
Ans. Such property is exhibited by a scalene triangle. As all three sides are of different lengths, the angles also differ. In the following diagram we can easily observe that all the angles are different and so are the sides.

Ques. What do you mean by a triangle? (3 Marks)
Ans. A triangle is basically a figure that has three sides, three vertices, and three angles. If you would take the sum of all the three angles of any triangle then it would be equal to 180° degrees. Triangle is a closed two-dimensional shape. It is a three-sided polygon. All aspects are made of straight traces. The factor where two straight traces are a part of is the vertex. Hence, the triangle has three vertices. Each vertex forms an angle.
Ques. What is an equilateral triangle? (3 Marks)
Ans. Triangle having all three similar sides is known as an equilateral Triangle. As all the three sides are the same, therefore the three respective angles are also the same. Hence each angle is 60°. Equilateral is formed with the aid of the combination of words, i.E., “Equi” that means identical and “Lateral” which means facets. An equilateral triangle is likewise called a regular polygon or normal triangle when you consider that all its aspects are identical.
Read More: Triangles Important Questions
Ques. What is the hypotenuse in a right angle triangle? (3 Marks)
Ans. A hypotenuse in a right angle triangle is the largest side of that triangle and is always opposite to the 90° angle. Although all the angles are less than 90°. In the following diagram we can witness that angle A and angle B join to form the hypotenuse and we can see it is the longest side of the triangle.

Also, read: Angle Between a Line and a Plane
Ques. What is an acute angle triangle? (3 Marks)
Ans. An acute angle triangle is a triangle having all three angles less than 90° each. Therefore all the angles of an acute angle triangle are called acute angles. We study an angle that measures much less than ninety degrees, i.e., much less than a right perspective is an acute attitude. In the diagram we can observe that each angle is less than 90°.It can be anything more than zero but less than 90°.

Also, read: Important Notes of Three-Dimensional Geometry
Ques. Mention the triangles based on their length of the sides? (3 Marks)
Ans. Triangles based on the length of their sides:
- Equilateral Triangle: Triangle in which all sides are equal are called equilateral triangle.

- Isosceles triangle: Triangle in which two sides are equal are called isosceles triangle.

- Scalene Triangle: Triangle in which no sides are equal are called scalene triangle.

Ques. Mention the triangles based on their internal angles? (3 Marks)
Ans. Triangles based on their internal Angles:
- Right angle Triangle: Triangle in which one of the angle is of 90 degree is called right angle triangle.

- Acute angle Triangle: Triangle in which all angles are less than 90 degree are called acute angle triangle.

- Obtuse/Oblique angle Triangle: Triangle in which all angles are greater than 90 degree is called obtuse angle triangle.

Ques. If ABC is a triangle where AB = 6 cm, BC=7 cm and AC = 8 cm, then find its perimeter? (2 marks)
Ans. Given, ABC is a triangle.
- AB = 6 cm
- BC = 7 cm
- AC = 8 cm
- As we know by the formula,
- Perimeter = Sum of all three sides
- P = AB + BC + AC
- P = 6 + 7 + 8
- P = 21 cm
Ques. Find the area of a triangle having sides 5 , 2 and 3 units length? (3 marks)
Ans. Use Heron’s formula to find the area of a triangle-
- Semiperimeter (s) = (a + b + c)/2
- s = (5 + 2 +3)/2
- s = 5
- Area of a triangle = √[s(s-a)(s-b)(s-c)]
- √[5(5-5)(5-2)(5-3)]
- 0 square units.
Ques. The measure of two angles of a triangle is 60 degree and 70 degree. What will be the measure of the third angle? (3 marks)
Ans. The measures of two angles of a triangle is calculated as follows:
- Sum of all three angles of triangle by angle sum property = 180 degree
- Sum of meausre of two angles are given as 60 degree and 70 degree
- So Sum = 180 - 60 -70
- Hence, the measure of the third angle = 50 degree
Ques. Find the lengths of the sides of a triangle, if its angles are in the ratio 2 : 1 : 3 and the circum-radius is 5 cm? (3 marks)
Ans. According to the problem, the angles of the triangle are in the ratio 2 : 1 : 3 hence, we assume that the angles are 2k, k, and 3k
i.e., A = 2k, B = k and C = 3k.
- A + B + C= 180°
- 2k + k + 3k = 180°
- 6k = 180°
- k = 30°
- Therefore, the angles of the triangle are:
- A = 60°, B = k = 30° and C = 3k = 90°
- The circum-radius = R = 5 cm.
Therefore, if the lengths of the sides of the triangle be a, b,c then
- A = 2 R sin A = 2 x 5 x sin 60° = 5√3 cm.
- B = 2 R sin B= 2 x 5 x sin 30° = 5 cm
- C = 2 R sin C = 2 x 5 x sin 90° = 10 cm.
Ques. One of the angles of a triangle is 60° and the other two angles are equal. Find these two angles? (3 marks)
Ans. The measures of two angles of a triangle is calculated as follows:
- Sum of all three angles of triangle by angle sum property = 180 degree.
- One of the angle is given as 60 degree
- Let other two angles be equal to x as both are equal
- So 60 + x + x = 180
- 2x = 180 – 60
- 2x = 120
- x = 60 degrees
- Hence, the measure of the two angles are 60 degree
Check-Out:







Comments