Types of Triangles: Important Terms, Scalene, Acute, and Obtuse Triangle

There are three types of triangles: Scalene Triangle, Isosceles Triangle, and Equilateral Triangle. Triangles form the foundation stone of geometry. Mainly, their utilisation is maximum in the field of architecture, construction, interior designing. Although, the concept of triangles holds crucial importance for those in the field of engineering. Triangles have several key advantages for architects, such as their commonality, structural soundness, and ease of use every day. A triangle’s strength comes from its shape, which spreads forces evenly. 

What is a Triangle?

A triangle is defined as a specific type of two dimensional polygon having only three sides, three vertices and three angles. Based on the lengths and measures of the sides and angles of a triangle, there are six basic types of triangles.

Triangles can have the same sides or they can have different sides. They can have the same angles or they can have different angles. Angles can be greater than, less than, or equal to 90 degrees.

A triangle having the same angle and different side length is known as a similar triangle. Therefore, the bigger triangle and the smaller triangle always have the same side ratio. The simplest polygon is the triangle. Polygons are closed, flat, two-dimensional shapes that have many corners. Three corners are necessary to make a polygon since one or two corners cannot form a closed shape.

Angle sum is the property of triangles that the sum of all internal angles equals 180°.

Important Terms Related to Triangles

Median: A median is the line segment connecting the vertex of the triangle to the midpoint of the opposite side of the triangle.

Angle Bisector: An angle bisector is also defined as the angle in an equilateral triangle or the non-congruent angle in an isosceles triangle.

Centroid: An intersection of a triangle’s medians (the lines connecting its vertex to its opposite vertex) is a triangle’s centroid. It divides each of the medians in the ratio 2:1, which means it is located at 13% of the distance between each side.

Altitude: A triangle’s altitude is formed by a line segment that crosses through its vertex and is perpendicular to the line containing its base. The extended base of the altitude is found where it crosses the altitude.

Orthocentre: A triangle's orthocentre is the intersection of the perpendiculars drawn from its vertices to its opposite sides.

Types of Triangles

Refer to the table below for the types of triangles and their properties.

Types	Name of Triangle	Properties of Triangles	Diagrams
On the basis of sides	Scalene Triangle	All sides are unequal  No two sides are the same length Each interior angle is different Not all sides are non congruent  The smallest side is one which is opposite to the smallest angle  The longest side is the one which is opposite to the longest angle No line of symmetry Cannot be bisected into two equal halves Each angle on a scalene triangle is half that of its opposite side when inscribed in a circle
On the basis of sides	Isosceles Triangle	Only two sides are equal Only one side is unequal The angles opposite to the equal sides of an isosceles triangle are equal Two sides are congruent One side in non congruent A congruent angle is an angle opposite to the equal sides Third unequal angle is an acute or obtuse Circumcentre lies inside its triangle if all three angles are acute Chords are the sides of the circumcentre
On the basis of sides	Equilateral Triangle	All sides are equal Each interior angle is of 60 degrees Median, altitude, angle bisector, perpendicular bisector lie at one line The angle bisector form the symmetry line of an equilateral triangle Each altitude is the median
On the basis of interior angles	Acute Triangle	All the angles are less than 90 degrees All angles are acute Circumcentre lies insides Angle bisector intersects incentre
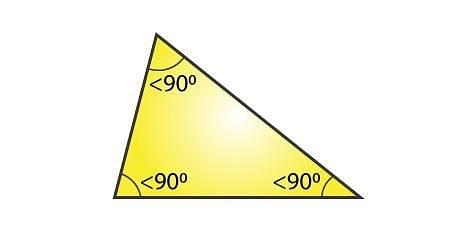On the basis of interior angles	Obtuse Triangle	One angle of all the angles is greater than 90 degrees Two acute angles  One obtuse angles Median intersect at the centroid Circumcentre lies outside
On the basis of interior angles	Right Triangle	One of the angles is equal to 90 ° Other two angles are acute  Hypotenuse is the side opposite to the right angle Perpendicular is the side next to 90 ° angle Base is the side on which triangle rests

Things to Remember

• An apex angle is a triangle whose two base angles are not congruent.
• Area, A = ½ × base × height
• By dividing the base in half and the apex angle in half, an isosceles triangle’s height is divided in half as well.
• From the median, we can get two equal sides. 
• Circumcentre lies outside the triangle, if the angle is 90°. 
• An isosceles triangle is divided into two equal triangles by the median.
• Median is the line which triangles into two. 
• Orthocentre, circumcentre, incenter and centroid coincide at the same point. 
• A circumcircle’s radius is always half its hypotenuse, and its centre is the hypotenuse’s midpoint.
• The right angle of the hypotenuse produces three similar triangles.