
Arpita Srivastava Content Writer
Content Writer
The operations on rational numbers are similar to basic arithmetic operations, which include addition, subtraction and multiplication. A rational number is defined as a number that can be written in the form of p/q, where p and q are integers and q ≠ is 0.
- The arithmetic operations on rational numbers can be solved in two different ways.
- First method involves an operation on numbers with the same denominator.
- The process becomes difficult when the operation is performed on numbers with different denominators.
- Rational numbers include all positive and negative integers.
- It also includes whole numbers, decimals and fractions.
- The real-life application of operations on rational numbers includes cooking recipes and financial transactions.
Key Terms: Operations on Rational Number, Rational Numbers, Addition, Subtraction, Multiplication, Division, Denominator, Numbers, Fraction, Decimal Numbers
What are Operations on Rational Numbers?
[Click Here for Sample Questions]
The arithmetic operations on rational numbers involve performing mathematical operations on two or more rational numbers. Like real numbers, arithmetic operations such as addition, subtraction, multiplication, and division are applicable to rational numbers.
- There are two types of categories: one with the same denominators and another with different denominators.
- Since a rational number is a fraction, therefore the denominator plays a crucial role in the operations.
- A rational number is said to be in standard form if p and q do not have any common factors other than 1.
- Here, p is a numerator and q is a denominator.
- A rational number is represented by “Q”.
The major arithmetic operations on rational numbers performed on rational numbers are:
- Addition of Rational Numbers
- Subtraction of Rational Numbers
- Multiplication of Rational Numbers
- Division of Rational Numbers
Example of Arithmetic Operations on Rational NumbersExample 1: Using the operations of rational numbers, determine the difference between −1/7 and 3/7. Solution: The given rational numbers have a common denominator. Thus, we will subtract the numerators and retain the same denominator. = −1/7−3/7 |

Operations on Rational Numbers
Read More:
Addition of Rational Numbers
[Click Here for Sample Questions]
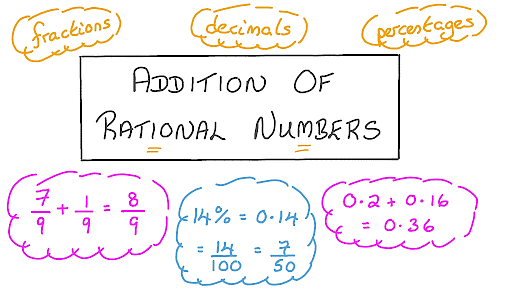
The most basic operations on rational numbers involves the addition of rational numbers. The addition of rational numbers involves adding rational numbers just like the addition of two integers.
- There are two cases involved in addition to rational numbers, which are as follows:
Addition of Rational Numbers with the same Denominators
Any two rational numbers in the form of p/q where q ≠ 0 can be added just like two integers. In other words, in addition to rational numbers with the same denominators, we add all the numerators and write the same denominators.
Example of Addition of Rational Numbers with same DenominatorsExample: To add the rational numbers 4/5 and 9/5, you just have to add the numerators since the denominator is common. Therefore, the result after adding the rational numbers as mentioned is
|
Addition of Rational Numbers with the different Denominators
Any two rational numbers with different denominators can be added by making the denominator the same, that is, taking out their LCM. The steps to add rational numbers with different denominators are as follows:
- First, determine the denominator of the given numbers.
- Take the common fractional value for the given set of rational numbers.
- Now, use the LCM rule and make the denominator common for numbers.
- Lastly, add the two rational numbers.
Example of Addition of Rational Numbers with the different DenominatorsExample: Consider the rational numbers 5/3 and 6/2. First, the LCM of denominators is to be carried out, so the LCM of 3 and 2 is 6. Next, add the rational numbers: 5/3 + 6/2 = 5 (2) + 6 (3)/6 Hence, 10+18/6 = 28/6 = 14/3 |
Addition of Rational Numbers
Subtraction of Rational Numbers
[Click Here for Sample Questions]
The second operations on rational numbers involves subtraction of two rational numbers. It is similar to the process of addition of rational numbers. The process of addition and subtraction can be carried on a number line.
- Like addition, there are two cases involved in addition to rational numbers, which are as follows:
Subtraction of Rational Numbers with same Denominators
Any two rational numbers in the form of p/q where q ≠ 0 can be subtracted just like two integers. In other words, in subtraction to rational numbers with the same denominators, we subtract all the numerators and write the same denominators.
Example of Subtraction of Rational Numbers with same DenominatorsExample: To subtract the rational numbers 7/5 and 4/5, you just have to subtract the numerators since the denominator is common. Therefore, the result after subtracting the rational numbers as mentioned is 7/5 - 4/5 = 3/5 |
Subtraction of Rational Numbers with different Denominators
Any two rational numbers with different denominators can be subtracting by making the denominator the same, that is, taking out their LCM. The steps to add rational numbers with different denominators are as follows:
- First, determine the denominator of the given numbers.
- Take the common fractional value for the given set of rational numbers.
- Now, use the LCM rule and make the denominator common for numbers.
- Lastly, subtract the two rational numbers.
Example of Subtraction of Rational Numbers with different DenominatorsExample: Consider the rational numbers 3/7 and 9/2 First the LCM of denominators is to be carried out, so LCM of 7 and 2 is 14. Next, subtract the rational numbers: Hence, Or, 3/7 - 9/2 = 3(2) - 9(7)/14 Or, 6 - 63/14 Or, -59/14 |

Subtraction of Rational Numbers
Multiplication of Rational Numbers
[Click Here for Sample Questions]
In order to multiply two rational numbers, there is no extra operation to be carried out rather just multiply like integers. The product of numerators and the product of denominators results in the multiplication of rational numbers.
Product of Rational Numbers = product of Numerator / Product of Denominator
Example of Multiplication of Rational NumbersExample: The multiplication of 3/2 and 9/4 is done as follows: 3/2 x 9/4 = 3 x 9/2 x 4 = 27/8 |

Multiplication of Rational Numbers
Division of Rational Numbers
[Click Here for Sample Questions]
Division of rational numbers is similar to the division of two fraction. Since rational numbers are written as fractions, therefore the divisor value can be reciprocated and multiplied by the numerator to carry out the division.
Dividend÷Divisor=Dividend/Divisor
Example of Division of Rational NumbersExample: 4/3 ÷ 2/5 becomes 4/3 x 5/2
|
Properties of Operations on Rational Numbers
[Click Here for Sample Questions]
The properties of operations on rational numbers are as follows:
Closure Property
The closure property states that the product of two rational numbers are always rational number. It is also a rational number.
Example of Closure PropertyExample: 5 x 8 = 40 is a rational number |
Commutative Property
Commutative Property states that when operations on rational numbers are performed on two numbers, then the result is commutative. It is given by
a x b = b x a
Example of Commutative PropertyExample: 6 x 8 = 48 is a rational number |
Associative Property
If a, b and c are three rational numbers, then it is given as a x (b x c) = (a x b) x c.
Example of Associative PropertyExample: 3 x (5 x 2) = 3 x 10 = 30 (3 x 5) x 2 = 15 x 2 = 30 Hence, 3 x (5 x 2) = (3 x 2) x 6. |
Distributive Property
When we insert the addition or subtraction sign in between two rational numbers and then multiply the third rational number with the addition or subtraction operator is equal.
Things to Remember
- Operations on rational numbers involve addition, subtraction, division and multiplication.
- A rational number is always written in the form p/q where q ≠ is 0.
- Addition and subtraction take place differently if the denominators are different.
- Closure, Commutative, and Associative properties are operations performed on rational numbers.
- Time and Distance is the common application of rational numbers.
Read More:
| Class 9 Mathematics Related Concepts | ||
|---|---|---|
| Polynomials | Quadratic Equations Formula | Degree of polynomial |
| Distance Formula | Section Formula | Pair of Linear Equations in Two Variables Formula |
Sample Questions
Ques: Add the rational numbers 3/2 and 9/2. (1 mark)
Ans: Since the denominators are the same, the numerators can be added directly.
Therefore, 3/2 + 9/2 = 12/2 = 6
Ques: Multiply the rational numbers 10/7 and 9/4. (1 mark)
Ans: 10/7 x 9/4 = 90/28 = 45/14
Ques: Divide the rational numbers 4/3 and 7/2. (1 mark)
Ans: 4/3 ÷ 7/2 = 4/3 ÷ 2/7 = 8/21
Ques: Subtract the rational numbers 8/12 and 5/12. (1 mark)
Ans: 8/12 - 5/12 = 8-5/12 = 3/12 = 1/4
Ques: Multiply the rational numbers 7/5 and 10/4. (1 mark)
Ans: 7/5 x10/4 = 70/20 = 7/2
Ques: Add the rational numbers 3/4 and 9/5. (2 marks)
Ans: Since the denominators are different, their LCM is needed.
LCM of 4 and 5 is 20.
Therefore, 3/4 + 9/5 = 3(5) + 9(4)/20
= 15 + 36/20
51/20
Ques: Subtract the rational numbers 15/2 and 5/3. (2 marks)
Ans: Since the denominators are not the same, we need LCM.
LCM of 2 and 3 is 6.
Therefore,
15/2 - 5/3 = 15(3) -5(2)/6 = 45-10/6 = 35/6
Ques: Divide the rational numbers 12/7 and 40/7. (1 mark)
Ans: 12/7÷ 40/7 = 12/7 ÷ 7/40 = 12/40 = 3/10
Ques: Add the rational numbers 3/4 and 3/2. (2 mark)
Ans: Since the denominators are different, find LCM to make the denominators same.
LCM of 4 and 2 is 2.
Therefore, 3/4 + 3/2 = 3(2) + 3(4)/4
= 6 + 12/4
= 18/4 = 9/2
Ques: Add the rational numbers 1/4 and 3/5. (2 marks)
Ans: Since the denominators are different, their LCM is needed.
- LCM of 4 and 5 is 20.
- Therefore, 1/4 + 3/5 = 1(5) + 3(4)/20
- 5 + 12/20
- 17/20
Ques: Subtract the rational numbers 7/2 and 5/3. (2 marks)
Ans: Since the denominators are not the same, we need LCM.
- LCM of 2 and 3 is 6.
- Therefore,
- 7/2 - 5/3
- 7(3) -5(2)/6
- 21-10/6
- 11/6
Ques: Divide the rational numbers 12/9 and 60/9. (1 mark)
Ans: 12/9÷ 60/9
= 12/9 ÷ 9/60
= 12/60
= 1/5
Ques: Add the rational numbers 3/4 and 5/8. (2 mark)
Ans: Since the denominators are different, find LCM to make the denominators same.
LCM of 4 and 8 is 8.
Therefore, 3/4 + 5/8 = 3(2) + 5(1)/8
= 6 + 1/8
= 7/8
Read Also:





Comments