
Arpita Srivastava Content Writer
Content Writer
Scalene Triangle is a type of triangle that has different lengths on all sides. This is one of the three types of triangles based on sides. In a scalene triangle, all the sides, as well as the angles,are unequal.
- The total interior angle of a scalene triangle is also 180 degrees.
- It follows the angle sum property of a triangle.
- It is classified into three types, namely acute, right angle and obtuse scalene triangle.
- A triangle is a three-sided polygon that is one of the basic shapes of the geometry.
- The scalene triangle does not follow the line of symmetry.
- Vertices are called zero-dimensional points.
- Sides are called one-dimensional line segments.
- Sailboats and mountain peaks are some real life examples of scalene triangle.
Read More: Equilateral Triangle
Key Terms: Scalene Triangle, Angle Sum property, Altitude, Height, Heron’s Formula, Right Angled Triangle, Acute Angled Scalene Triangle, Obtuse Angled Scalene Triangle, Area of Scalene Triangle, Perimeter of Scalene Triangle
What is a Scalene Triangle?
[Click Here for Sample Questions]
A scalene triangle has three sides of varying lengths and three angles of varying measures. In this, the sum of all the interior angles is always equal to 180 degrees. Therefore, it meets the angle sum property requirements for a triangle.
- Scalene Triangle is derived from a Greek word named Skalinon, which means unequal.
- The below figure explains the concept of the scalene triangle.
- Three sides are represented by three different tick marks, indicating that the three sides are not equal.
- Similarly, three angles are represented by different marks, indicating angles are varying.
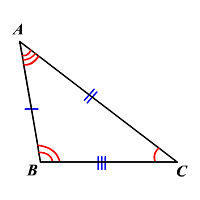
Solved Example of Scalene TriangleExample: Since the sides of a triangle are given as 19 cm, 23 cm, and 14 cm, can we say that it is a scalene triangle? Solution: All three sides of the triangle are of different measures, 19 cm, 23 cm, and 14 cm. Therefore, we can say that it is a scalene triangle |
Read More:
Types of Scalene Triangle
[Click Here for Sample Questions]
Several types of Scalene triangle can be distinguished depending on their sides and angles. According to their interior angles, Scalene triangle can be divided into three categories, which are as follows:
Right Angled Scalene Triangle
A scalene triangle where one of the angles is a right angle or 90 degrees is known as a right-angled scalene triangle. The corresponding sides containing the right angle would be perpendicular to each other. It does not contain any equal sides.
Read More: Trapezoid Formula
Acute Angled Scalene Triangle
A scalene triangle where one of the angles is acute or below 90 degrees is called an acute angled scalene triangle. It does not contain any equal sides and consists of three acute angles.
Obtuse Angled Scalene Triangle
A scalene triangle where one of the angles is obtuse or above 90 degrees is called an obtuse angled scalene triangle. It does not contain any equal sides and consists of one obtuse angle.
Read More: Area of Rectangle
Properties of Scalene Triangle
[Click Here for Sample Questions]
Some of the important properties of scalene triangle are as follows:
- Scalene triangles have no equal sides and angles.
- There is no line of symmetry and point of symmetry.
- The centre of the circumscribing circle will lie inside a triangle if all of the angles are smaller than 90° (acute).
- The circumcentre of a scalene obtuse triangle lies outside the triangle.
- Scalene triangles can be obtuse-angled, acute-angled, and right-angled.
- An angle opposite to a triangle's longest side will be its greatest angle.
Read More: Congruence of Triangles
Formulas of Scalene Triangle
[Click Here for Sample Questions]
Area and Perimeter are the two parameters to consider for the measurements of scalene triangle. The important formulas related to scalene triangle are as follows:
Area of a Scalene Triangle
Heron’s formula is characterized by the use of length of the sides and semi parameters of the scalene triangle. Heron’s formula is as follows for area of a scalene triangle is as follows:
A= √s(s−a)(s−b)(s−c) sq. units
- where, a, b, c → Length of sides of Triangle
- s → Semi perimeter of Triangle
- The formula of semi perimeter of a triangle is given by,
s = (a+b+c)/2 units
Solved Example of Area of a Scalene TriangleExample: Find the area of a scalene triangle XYZ in which side X= 5 cm, side Y = 5 cm and side Z = 4 cm. Ans: Given, X = 5 cm Y = 5 cm Z = 4 cm All the sides are given, hence, we can apply Heron’s formula here. Area of triangle = √s(s−a)(s−b)(s−c) s = (a+b+c)/2 s= (5+5+4)/2 s= (14)/2 s= 7 cm Substituting the values in the formula, we get Area of a triangle XYZ = √7(7-5)(7-5)(7-6) =√7(2)(2)(1) =2√7 So, the area of triangle XYZ is 2√7 cm. |
Read More: Construction Formula
Using Altitude Formula
If the length of its base and corresponding altitude/height is given, we can calculate the area of the triangle by using the altitude formula. The altitude formula fpr scalene triangle is given by,
A = (1/2) x b x h sq.units
- where, b → Base length of the triangle
- h → Altitude/ height of the triangle
Solved Example using Altitude FormulaExample: The area of a triangle is 64 square units. Find the length of the altitude if the length of the base is 8 units. Solution: We know that altitude of a triangle, h = (2 × Area) / Base. |
Read More: Difference between Area and Volume

Using Angle Formula
If the length of two sides and angle between them is given, we can calculate the area of the triangle by multiplying the given sides with the sine of the angle between them.
A = (1/2) × a × b × sin c sq.units
- where,a, b, c → Length of side of the Scalene triangle
Solved Example using Angle FormulaExample: Find the area of triangle ABC, given that the sides AB = 6 units, BC = 8 units and ∠ABC = 60°. Solution: Length of AB = c = 6 units, Length of BC = a = 8 units Angle between AB and BC = ∠B = 60° Area ΔABC = 1/2 × a × c × sin(B) = 1/2 × 6 × 8 × sin60º = 12 √ 3 square units |
Read More: Area of Parallelogram
Perimeter of a Scalene Triangle
Perimeter of a scalene triangle is equal to the sum of the lengths of its sides, and it is calculated as follows:
Perimeter P = a + b + c Units
- where, a, b, c → Length of side of Scalene Triangle
Solved Example of Perimeter of a Scalene TriangleExample: If the sides of a triangle XYZ are 11 cm, 25 cm and 23 cm. Find the perimeter of the triangle. Ans: Given Length of side X = 11 cm Length of side Y = 25 cm Length of side Z = 23 cm Perimeter = Sum of all sides = 11 + 25 + 23 = 59 cms |
Read More:
Things to Remember
- Scalene triangle has three sides of varying lengths and three angles of varying measures.
- Areas is the measure of space occupied by an object within a two-dimensional plane.
- There are three types of scalene triangles, namely, right-angled scalene triangle, obtuse-angled scalene triangle and acute-angled scalene triangle.
- The area of a triangle can be calculated using Heron’s formula and the angle formula.
- Perimeter of a scalene triangle is calculated by adding all the lengths of the sides of the triangle.
Read More: Types of Angle
Sample Questions
Ques: Justify whether or not the scalene triangle justifies the angle sum property. (2 marks)
Ans: Just like all the triangles in geometry, the scalene triangle has a different measure. Also, the sum of three interior angles of a triangle equals 180 degrees.
Ques: Define a right scalene triangle. (2 marks)
Ans: Right angled scalene triangle is a triangle in which the measure of any one side equals 90 degrees. While, the measure (length) of the remaining sides are not concurrent. The corresponding sides containing the right angle would be perpendicular to each other. It does not contain any equal sides.
Ques: If the sides of a triangle XYZ are 10 cm, 15 cm and 23 cm. Find the perimeter of the triangle. (3 marks)
Ans: Given
Length of side 1,X = 10 cm
Length of side 2,Y = 15 cm
Length of side 3,Z = 23 cm
Perimeter = Sum of all sides
= 10 + 15 + 23 = 48 cms
Ques: How many types of triangles are there in general. (3 marks)
Ans. In general, there are three types of triangles which are as follows:
- Equilateral Triangle – In equilateral triangle, all three sides and angles are equal.
- Isosceles Triangle – In isosceles triangle, two sides and angles are equal.
- Scales Triangle – In scalene triangle, all sides and angles are different.
Ques: State the differences between Scalene and Isosceles Triangle. (3 marks)
Ans. The difference between scalene and isosceles triangle are as follows:
| Scalene Triangle | Isosceles Triangle |
|---|---|
| In a scalene triangle, all the sides and corresponding angles are different. | In an Isosceles triangle, two sides and corresponding angles are equal. |
| Scalene triangle is of three types- right angles, obtuse and acute. | Isosceles triangle is also divided into right angled, obtuse angled and acute angled. |
| An angle opposite to a triangle's longest side will be its greatest angle. | The side opposite to the equal side is the longest one. |
Ques: Find the area of a scalene triangle XYZ in which side X= 5 cm, side Y = 5 cm and side Z = 6 cm. (4 marks)
Ans: Given,
X = 5 cm
Y = 5 cm
Z = 6 cm
All the sides are given, hence, we can apply Heron’s formula here.
Area of triangle = √s(s−a)(s−b)(s−c)
s = (a+b+c)/2
s= (5+5+6)/2
s= (16)/2
s= 8 cm
Substituting the values in the formula, we get
Area of a triangle XYZ = √8(8-5)(8-5)(8-6)
=√8(3)(3)(2)
=√8(18)
=√144
=12
So, the area of triangle XYZ is 12 cm.
Ques. ABC and DBC are isosceles triangles on the same base BC (see figure). Show that ∠ ABD = ∠ACD. (3 marks)

Ans. In ΔABC, we have
AB = AC [ABC is an isosceles triangle]
∴ ∠ABC = ∠ACB …(1)
[Angles opposite to equal sides of a Δ are equal]
Again, in ΔBDC, we have
BD = CD [BDC is an isosceles triangle]
∴ ∠CBD = ∠BCD …(2)
[Angles opposite to equal sides of a A are equal]
Adding (1) and (2), we have
∠ABC + ∠CBD = ∠ACB + ∠BCD
⇒ ∠ABD = ∠ACD
Ques. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see figure). Show that these altitudes are equal. (4 marks)

Ans. ΔABC is an isosceles triangle
∴ AB = AC
⇒ ∠ACB = ∠ABC [Angles opposite to equal sides of a A are equal]
⇒ ∠BCE = ∠CBF
Now, in ΔBEC and ΔCFB
∠BCE = ∠CBF [Proved above]
∠BEC = ∠CFB [Each 90°]
BC = CB [Common]
∴ ΔBEC ≅ ΔCFB [By AAS congruency]
So, BE = CF [By C.P.C.T.]
Ques. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠BCD is a right angle. (5 marks)
Ans. AB = AC [Given] …(1)
AB = AD [Given] …(2)
From (1) and (2), we have
AC = AD
Now, in ΔABC, we have
∠ABC + ∠ACB + ∠BAC = 180° [Angle sum property of a A]
⇒ 2∠ACB + ∠BAC = 180° …(3)
[∠ABC = ∠ACB (Angles opposite to equal sides of A are equal)]
Similarly, in ΔACD,
∠ADC + ∠ACD + ∠CAD = 180°
⇒ 2∠ACD + ∠CAD = 180° …(4)
[∠ADC = ∠ACD (Angles opposite to equal sides of a A are equal)]
Adding (3) and (4), we have
2∠ACB + ∠BAC + 2 ∠ACD + ∠CAD = 180° +180°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2∠BCD +180° = 360° [∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360° – 180° = 180°
⇒ ∠BCD = 180°/2 = 90°
Thus, ∠BCD = 90°
Ques. In ΔABC, AD is the perpendicular bisector of BC (see figure). Show that ΔABC is an isosceles triangle in which AB = AC. (3 marks)

Ans. Since AD is the bisector of BC.
∴ BD = CD
Now, in ΔABD and ΔACD, we have
AD = DA [Common]
∠ADB = ∠ADC [Each 90°]
BD = CD [Proved above]
∴ ΔABD ≅ ΔACD [By SAS congruency]
⇒ AB = AC [By C.P.C.T.]
Thus, ΔABC is an isosceles triangle.
Ques. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at 0. Join A to 0. Show that (4 marks)
(i) OB = OC
(ii) AO bisects ∠A
Ans. i) in ΔABC, we have
AB = AC [Given]
∴ ∠ABC = ∠ACB [Angles opposite to equal sides of A are equal]

⇒ 1/2∠ABC = 1/2∠ACB
or ∠OBC = ∠OCB
⇒ OC = OB [Sides opposite to equal angles of a Δ are equal]
(ii) In ΔABO and ΔACO, we have
AB = AC [Given]
∠OBA = ∠OCA [ ?1/2∠B = 1/2∠C]
OB = OC [Proved above]
ΔABO ≅ ΔACO [By SAS congruency]
⇒ ∠OAB = ∠OAC [By C.P.C.T.]
⇒ AO bisects ∠A.
Ques. The length of the sides of a scalene triangle ABC are 4 units, 4 units, and 6 units. Calculate its area. (3 marks)
Ans. Let a = 4 units, b = 4 units, c = 6 units .
Using Heron's Formula:
Area of triangle = √[s(s-a)(s-b)(s-c)].
We will first find the semi perimeter 's'
s = (a+b+c)/2
⇒ s = (4+4+6)/2
⇒ s = 7.
Now, let us substitute the values in the formula.
Thus, Area of scalene triangle
= √[7(7-4)(7-4)(7-6)]
= √(7(2)(2)(1))
= 2√(7)
Therefore, the area of the triangle is 2√(7) units2.
Ques: If the sides of a triangle XYZ are 16 cm, 18 cm and 20 cm. Find the perimeter of the triangle. (3 marks)
Ans: Given
Length of side 1,X = 16 cm
Length of side 2,Y = 18 cm
Length of side 3,Z = 20 cm
Perimeter = Sum of all sides
= 16 + 18 + 20 = 54 cms
Ques. Find the length of the third side of a scalene triangle with two side lengths of 13 cm and 17 cm and a perimeter of 50 cm. (3 marks)
Ans. We have,
- a = 13
- b = 17
- P = 50
- Using the Perimeter Formula
- Perimeter (P) = (a + b + c)
- P = (a + b + c)
- 50 = (13 + 17 + c)
- 50 = 30 + c
- c = 20 cm
- Thus, the required length of third side of the triangle is 20 cm
Ques. Find the area of a scalene triangle with side lengths of 8 cm, 4 cm, and 8 cm. (3 marks)
Ans. We have,
- a = 8
- b = 4
- c = 8
- Semi-Perimeter (s) = (a + b + c)/2
- s = (8 + 4 + 8)/2
- s = 20/2
- s = 10 cm
- Using the Heron’s formula
- Area = √(s(s – a)(s – b)(s – c))
- A = √(10(10 – 8)(10 – 4)(10 – 8))
- A = √(10(2)(6)(2))
- A = 4√15
- A = 4√15 sq. cm
- Thus, the required area of the scalene triangle is 4√15 cm2
Ques. Find the area of a scalene triangle whose base is 10 cm and altitude is 10 cm. (3 marks)
Ans. We have, b = 10
- h = 10
- Area of Scalene Triangle (A) = 1/2 × b × h
- ⇒ A = 1/2 × 10 × 10
- ⇒ A = 50 sq. cm
- Thus, the area of the given scalene triangle is 50 sq. cm.
Read Also:





Comments