
Content Curator
Triangles are closed polygons with three sides. These are formed when three lines intersect. It is a fundamental geometric shape. Three sides, three angles, and three vertices make up the triangle. The sum of all the three angles in a triangle is always equal to 180°. The length of the sides of a triangle can be the same or different. The total length of the sides of a triangle is known as it’s perimeter. It's the sum of all the sies or edges of a triangle.
Therefore, the Perimeter of a triangle is:
Perimeter = Sum of all three sides
| Table of Content |
Key Takeaways: Triangles, Perimeter, Equilateral, Scalene, Isosceles
Types of Triangles
[Click Here for Sample Questions]
Triangles are classified into three categories based on their sides:
- A triangle that has all three sides of equal length is known as an equilateral triangle. All angles in an equilateral triangle are of 60o.
- An isosceles triangle is defined as a triangle with any two sides that are equal. The vertices opposing the equal sides of an isosceles triangle have two equal angles.
- A Scalene Triangle is one in which the lengths of all three sides are varied. As a result, the angles have varied measurements.
Also Check: Types of Triangles
Properties of Triangles
[Click Here for Sample Questions]
The key properties of triangles are mentioned below:
- A triangle has three sides, which can be of the same length or different.
- The length of the third side of a triangle is always greater than the sum of the length of the other two sides.
- The difference between any two sides of a triangle is always lesser than the third side of the triangle.
- The total measure of the three angles of a triangle would always be equal to 180 degrees.
- The exterior angle of the third side of a triangle is equal to the sum of two internal angles.
Certain requirements must be met in order for a triangle to exist. One of the following three conditions must be true for any triangle.
- a + b > c
- b + c > a
- c + a > b
Also Read: Congruence of Triangles
Perimeter of a Scalene Triangle
[Click Here for Sample Questions]
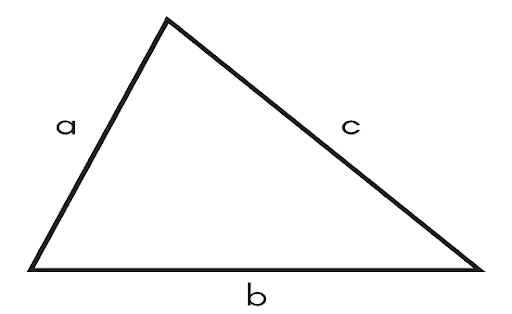
A triangle's perimeter is the total sum of all its sides. If a, b, and c are the lengths of the triangle's sides, then:
Scalene triangle perimeter = a + b + c
where,
a, b and c are the lengths of the three sides of the triangle.
Perimeter of an Isosceles Triangle
[Click Here for Sample Questions]
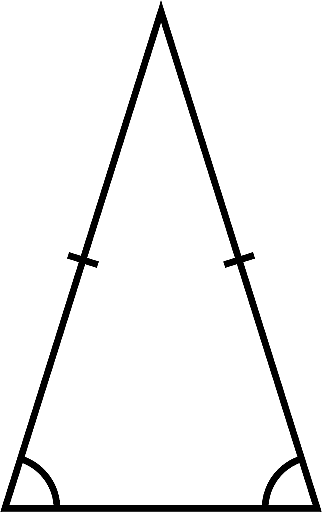
If two equal sides of an isosceles triangle are of length 'a’ units and the length of an unequal side is equal to 'b', then:
Isosceles triangle perimeter = a + a + b = 2a + b
where,
The length of two equal sides is a and the third side length is b.
Perimeter of an Equilateral Triangle
[Click Here for Sample Questions]
All sides of an equilateral triangle are of the same length, therefore a = b = c.
Hence,
Equilateral triangle perimeter = a + a + a = 3a
where,
The side length is denoted by the letter a.

Read: Triangles Important Questions
Things to Remember
- Triangles are two-dimensional polygonal figures with three sides and three angles.
- The perimeter of a triangle is the total length of its sides.
- The perimeter of a Triangle = Sum of the lengths of all sides of the triangle.
- There are three types of triangles: Equilateral, Scalene, and Isosceles.
Sample Questions
Ques.: What is the perimeter of a triangle whose sides are 4cm, 5cm, and 6cm in length? (2 marks)
Ans.: The triangle's sides are 4cm, 5cm, and 6cm, respectively. As a result, it's a scalene triangle.
Therefore, the triangle's perimeter equals the sum of its sides, which is 4 + 5 + 6 = 15cm.
Ques.: If the length of the unequal side is 5cm and the perimeter is 17cm, find the length of two equal sides of an isosceles triangle. (3 marks)
The unequal side's length is 5cm, and the perimeter is 17cm.
Ans.: Because it's an isosceles triangle, the lengths of the other two sides are the same. Let’s consider 'a' units to be equal side length of the triangle.
As a result, perimeter = a + a + 5
We can write, (since the perimeter is 17cm)
a + a + 5 = 17
17 = 2a + 5
12 = 2a
12 = 2a
As a result, the equal sides of the isosceles triangle are 6cm long.
Ques.: Calculate the perimeter of a triangle with 6 cm, 8 cm, and 12 cm sides. (2 marks)
Ans.: Assume a = 6 cm, b = 8 cm, and c = 12 cm.
Triangle Perimeter = a + b + c
= 6 + 8 + 12
= 26 cm
Ques.: Calculate the perimeter of an equilateral triangle with a 6 cm side. (2 marks)
Ans.: All of the sides of an equilateral triangle are equal.
As a result, the equilateral triangle's perimeter = a + b + c
= a + a + a
= 3a
= 3 x a
= 3 x 6
= 18 cm
Ques.: What is the perimeter of an equilateral triangle with one 5cm side? (2 marks)
Ans.: Because the triangle is an equilateral triangle, the lengths of all three sides are equal.
Because one side is 5cm in length, the other two sides will be 5cm in length as well.
As a result, the perimeter is calculated as 5 + 5 + 5 = 15cm.
Ques.: Find the lengths of the three sides of an equilateral triangle with a perimeter of 21cm. (2 marks)
Ans.: Because all three sides of an equilateral triangle are the same length, the perimeter is three times the length of a side.
Let any side's length be equal to 'a' units. As a result, perimeter equals '3a' units.
3a = 21 cm
a = 7 cm
Thus, each side measures 7 cm in length.
Ques.: Calculate the perimeter of a triangle with 10 cm on each side. (2 marks)
Ans.: The triangle is an equilateral triangle because all three sides are the same length.
a = b = c = 10 cm, for example
Perimeter = a + b + c
= 10 + 10 + 10
= 30 cm
Ques.: In a triangle with a perimeter of 40 cm and two sides of 10 cm each, what is the missing side length? (3 marks)
Ans.: Assume that the perimeter is 40 cm.
Both sides are the same length, i.e., 10 cm.
As a result, the triangle is isosceles.
Using the formula:
P = 2l + b
40 = 2 * 10 + b
40 = 20 + b
or
b = 20
The length of the missing side is 20 cm.
Ques.: Calculate the perimeter of a triangle with 5 cm, 4 cm, and 2 cm sides. (3 marks)
Ans.: Let's assume a = 5 cm, b = 4 cm and c = 2cm.
Perimeter = Sum of all sides
= a + b + c
= 5 + 4 + 2 = 11 cm
As a result, the correct answer is 11 cm.
Ques.: Find the perimeter of an isosceles triangle with 6 cm equal sides and an 8 cm third side. (2 marks)
Ans.: Two sides of an isosceles triangle are equal.
As a result, a = 6, b = 6, and c = 8
Isosceles triangle perimeter = a + b + c
= a + a + c
= 2a + c
= 2 x 6 + 8
= 12 + 8
= 20 cm
Ques.: A triangle's longest side is twice as long as its shortest side. If the length of the third side is 15 cm and the perimeter is 57 cm, find two missing sides. (5 marks)
Ans.: Let a be one of the triangle's sides.
The opposing side, as per the question, will be:
b = 2a
c = 15 cm (given)
Perimeter = a + b+ c
57 = a + 2a + 15
57 = 3a + 15
57- 15 = 3a
42 = 3a
a = 42/3
a =14
Also,
b= 2a
= 2 x 14
= 28
Hence, a = 14 cm, b = 28 cm
Therefore, the two sides are 14 cm and 28 cm respectively.
Also Check:





Comments