Triangles Revision Notes

A triangle is a three-sided closed polygon, which has three vertices. The three sides are connected with each other end to end at a point, which forms the angles of the triangle. The sum of all three angles of a triangle is equal to 180^o.

Key Terms: Triangle, Types of triangle based on sides, Types of triangle based on angles, different types of triangles, area of trianles

---

What is a Triangle?

[Click Here for Sample Questions]

A triangle is a figure which has three sides and three angles. The sum of the inner angles of a triangle will always be 180^o and the sum of the external angles put together will always be 360^o

.

Symbol used to represent the Triangle: Δ.

In this chapter, we’ll discuss the types and various properties of Triangles.

Contents of the Chapter:

• Types of Triangles
• Similarity Criteria(s) of Triangles
• Properties of Triangles
• Area of Similar Triangles
• Pythagoras Theorem
• Summary and key points
• Sample/Previous Years NCERT questions

---

Types of Triangles

[Click Here for Sample Questions]

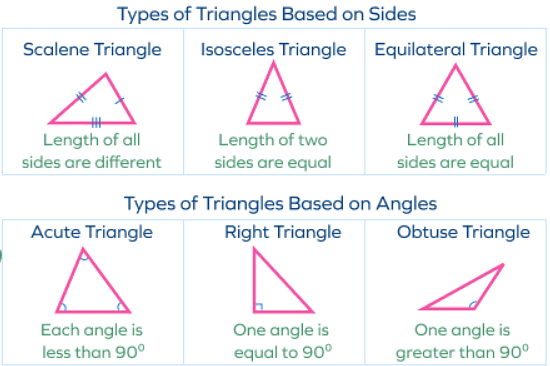
Types of Triangles based on Sides:

Scalene Triangle

If all the three sides of a triangle are of different measures or can be said that all are not equal, then the triangle is Scalene Triangle.

Isosceles Triangle

The triangle is said to be isosceles if any two sides of the triangle are equal.

Equilateral Triangle

A triangle is said to be equilateral if all the three sides of a triangle are equal and each angle measures 60 degrees.

Types of Triangles Based on Angles:

Acute Angle Triangle

Acute Triangle is a triangle in which all the angles are less than 90 degrees.

Right Angle Triangle

When any one side of a triangle is equal to 90^o, it is called a right-angled triangle. The other two angles of a right-angle triangle are acute angles and the side opposite to the right angle is the largest side of the triangle and is called the hypotenuse.

Obtuse Angle Triangle

A triangle is said to be an Obtuse Angle Triangle if any one of the angles is greater than 90 degrees.

Thus, we can easily observe the different types of triangles based on sides and angles

Associated Theorems

Two triangles are similar, if:

• Their corresponding angles are equal and,
• Their corresponding sides are in the same ratio.

Theorem 1:

If a line is drawn parallel to one side of a triangle to interface the other two sides in distinct points, the other two sides are divided in the same ratio.

Theorem 2: 

If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.

Theorem 3:

If in two triangles, sides of one triangle are proportional to the sides of the other triangle, then their corresponding angles are equal and hence two triangles are similar.

Theorem 4:

If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

Theorem 5:

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

---

Properties of Triangles

[Click Here for Sample Questions]

The various Properties of Triangles are as follows:

• A Triangle has three sides, three angles and three vertices but all can be altered.
• The sum of all the internal angles of a triangle is always equal to 180 degrees. This is called the Angle Sum Property of a triangle.
• The sum of the length of any two sides of a triangle is greater than the length of the third side.
• The side opposite to the largest angle of a triangle is the largest side.
• Any exterior angle of the triangle is equal to the sum of its interior opposite angles. This is called the Exterior Angle Property of a triangle and it is equal to 360 degrees.

---

Area of Similar Triangles

[Click Here for Sample Questions]

Two triangles are similar when certain conditions are met:

• Corresponding angles of the triangles are equal.
• Corresponding sides of the triangle are proportional to each other.

Theorem: If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.

To prove this theorem, take two triangles  ΔABCand  ΔPQR,

 Area of one triangle Is divided by the area of the second triangle to find the similarity of the triangles.

For example – let's assume a triangle has area which is equal to X and another triangle whose area is equal to Y. the, Area of similarity can be calculated as:

Area = X/Y.

Formulas for Calculating Area of Triangles:

• Area of triangle = ½ * base * height
• Area of right-angled triangle = ½ * product of two perpendicular sides of a triangle.

Pythagoras’ Theorem

The Pythagoras theorem states that in a right-angled triangle, the sum of squares of two sides of a triangle is equal to the square of the hypotenuse of a triangle. (In Pythagoras theorem, there is no concept of similarity)

Concept of Pythagoras Theorem can be defined by taking an example of a right-angled triangle having base, hypotenuse and perpendicular(height). The consumptions taken are base=a; perpendicular = b; and hypotenuse

= c. The formula derived is:

(base)² + (perpendicular)²  = (hypotenuse)² 

 (a)² + (b)² = (c)² 

Hypotenuse: The longest side of a right-angle triangle, opposite the right angle.

---

Things to Remember

• The sum of all interior angles of any triangle is equal to 180 degrees.
• The sum of all exterior angles of any triangle is equal to 360 degrees.
• An exterior angle of a triangle is equal to the sum of its two interior opposite angles.
• The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
• Similarly, the difference between the lengths of any two sides of a triangle is always less than the length of the third side.
• The side opposite to the smallest interior angle is the shortest side and vice versa.
• Similarly, the side opposite to the largest interior angle is the longest side and vice versa. (In the case of a right angled triangle, this side is called the hypotenuse).
• The height of a triangle is equal to the length of the perpendicular measured from the vertex to the opposite side of the triangle, and this side is considered as the base.