Types of Quadrilaterals: Definition, Properties & Examples

A Quadrilateral is a closed shape that is known to have sides of different measures and different lengths. It is a two dimensional closed shaped polygon having four vertices, four angles and four sides. Trapezium, Parallelogram, Rectangle, Rhombus, Square and Kite are some of the examples of Quadrilateral. 

The concept of quadrilateral was introduced by the Greek Mathematician, Euclid in his Euclidean Plane Geometry. The word quadrilateral has been derived from two separate Latin words- “Quadri” which means ‘a variant of four’ and “latus” which means ‘side’. Quadrilaterals can be both simple and complex-type. If we consider any quadrilateral, say ABCD, then the sum of all its interior angle (of a simple quadrilateral) will be 360°. This is known as the Angle Sum Property of a Quadrilateral. There are various types of Quadrilaterals such as Trapezium, Parallelogram, Rectangle, Rhombus, Square and Kite.

Key Terms: Quadrilateral, Polygon, Shape, Vertices, Side, Angles, Parallelogram, Rectangle, Trapezium, Rhombus, Square, Kite, Properties, Edges, Symmetry

---

What is a Quadrilateral? 

[Click Here for Sample Questions]

A Quadrilateral can be defined as a polygon with 4 vertices and 4 sides enclosing 4 angles. The sum total of all the interior angles of a quadrilateral is 360 degrees which means

 ∠A+ ∠B+∠C+ ∠D = 360°

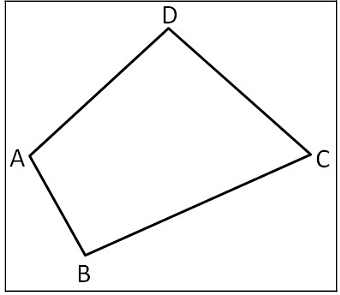
Quadrilateral

---

Types of Quadrilaterals

[Click Here for Sample Questions]

Based on the different sides, angles, edge and vertices formed by quadrilaterals, there are six different variants of quadrilaterals present in geometry, they are:

• Parallelogram
• Trapezium
• Rhombus
• Kite
• Rectangle
• Square

Types of Quadrilateral

---

Properties of Quadrilaterals

[Click Here for Sample Questions]

The various types of quadrilaterals and their properties are:

Parallelogram

A parallelogram is a kind of quadrilateral that has both its sides parallel to each other. The sides and lengths of a parallelogram will be always equal to each other. Let us consider a parallelogram ABCD, and here we can see that AB and CD are equal sides, then AB=CD.

If we draw two diagonals AC and BD, we see that the diagonals intersect each other at their mid-points. If we name the mid-point as E, the length AE=CE and BE=DE

The consecutive angles of parallelogram ABCD will be supplementary opposite angles of the parallelogram will also be equal, i.e. 180°.

• Number of vertices present: 4
• Number of edges present: 4
• Area: Height x Base
• Perimeter: 2 x sum of the lengths of adjacent sides
• Line of symmetry: 0
• Properties A Parallelogram has parallel and congruent opposite sides. The diagonals intersect each other at a midpoint. Hence, the opposite angles are congruent and also equal.

Parallelogram

Check More: Introduction to Three-Dimensional Geometry

Trapezium

A trapezium is a quadrilateral that has one side parallel to its opposite side. Let us consider a trapezium ABCD, where side AB is parallel to side CD.

• Number of vertices present: 4
• Number of edges present: 4
• Line of symmetry: 0
• Area: ½ x perpendicular distance x sum of the lengths of parallel sides
• Properties: When the one set of opposite sides is parallel to each other, the sum of the adjacent angles for a convex polygon will be 180°.

Trapezium

Rhombus

Rhombus is a kind of quadrilateral with all four sides of equal lengths. Here, the opposite angles are equal and the opposite sides are parallel to each other.

• Number of Edges: 4
• Number of Vertices: 4
• Area: pq/2, [p and q are the two diagonals]
• Perimeter: 4 x side of the rhombus
• Properties: In a closed convex polygon, where the diagonals are congruent, perpendicular and intersect each other, the opposite angles are equal.

Rhombus

Kite

Kite is another type of 2-D shape which is having two pairs of equal sides and four edges. The sides of a kite are adjacent to each other. This type of shape can be concave or convex.

• Number of Edges: 4
• Number of Vertices: 4
• Area: ½ x product of the length of the diagonals
• Line of Symmetry: 1
• Rotational symmetry: 1
• Perimeter: 2 x sum of the length of sides
• Properties: A rhombus has two consecutive sides & congruent pairs, perpendicular diagonals and congruent non-vertex angles.

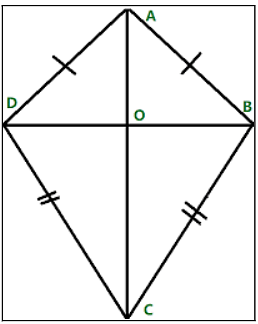
Kite

Rectangle

In the case of a rectangle, it has all the four angles of the same measure, right angles i.e. 90°. The opposite sides of a rectangle are parallel to each other and are of the same lengths. It is also said to be a parallelogram as all its interior angles are right angles.

• Number of Edges: 4
• Number of Vertices: 4
• Area: Length x Breadth
• Perimeter: 2 x (Length + breadth)
• Internal Angles: 90°
• Properties:
  1. All the four angles are - 90°
  2. Opposite sides are equal and parallel to each other
  3. Diagonals bisect each other

Rectangle

Square

A type of Quadrilateral that has all its four sides equal, i.e. 90° is called a square. It is also said to be flat-shaped which looks like a rectangle having equal lengths of its two adjacent sides.

• Number of Edges: 4
• Number of Vertices: 4
• Area: (Side)2
• Perimeter: 4 x side
• Internal Angles: 90°

Properties:

• Diagonals are equal
• All four sides are also equal
• The four angles have an equal measure that is 90°
• Opposite sides have equal lengths and are parallel to each other
• Diagonals bisect each other and meet at an angle of 90°
• The diagonals bisect its angles

Square

Read More: Difference between Area and Volume

Things to Remember

• A closed shape having 4 sides is termed a Quadrilateral.
• Quadrilateral consists of all the internal angles whose sum is 360°
• The properties of a quadrilateral are what help it to differentiate it from the other types of polygons
• Trapezium, Parallelogram, Rectangle, Rhombus, Square and Kite are examples of Quadrilateral.
• Different types of Quadrilaterals have different properties as mentioned above. 

---