
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Kite is a 2-dimensional geometric figure which consists of two pairs of triangles of equal size. The sum of all the sides of the kite is called the perimeter of the kite. The perimeter of the kite can be calculated by adding the sides of each pair. Kite can also be referred to as a quadrilateral with two adjacent sides of equal length. Hence perimeter of a kite is twice the sum of the length of two sides i.e 2(a+b). Kite and rhombus are often confusing. But the major difference between a kite and a rhombus is that all the sides of a rhombus are equal, unlike a kite.
| Table of Contents |
Key Takeaways: Geometry, Kite, Perimeter, Quadrilaterals, rhombus, perimeter of a kite, perimeter of kite formula.
What is a kite?
[Click Here for Sample Questions]
In Euclidean Geometry, a kite is a 2-dimensional quadrilateral in which four sides of the figure are joined to form a pair of parallel lengths. In contrast, a parallelogram also has two pairs of sides that are equal in length, but opposite rather than parallel.

A kite
Also read: Area of parallelogram
- Kite quadrilaterals are named after a wind, flying kites, often with this shape and named after a bird. Kites are also known by another name-” deltoids”.
- The kite, as described above, may be convex or concave, but the word "kite" is usually limited to convex varieties. The concave kite is sometimes called a "dart" or "arrowhead", and is a type of pseudotriangle.
Read more about types of polygon
Formula for Perimeter of Kite
[Click Here for Sample Questions]
The perimeter of a kite is defined as twice the sum of length a and b units as shown in the diagram below:
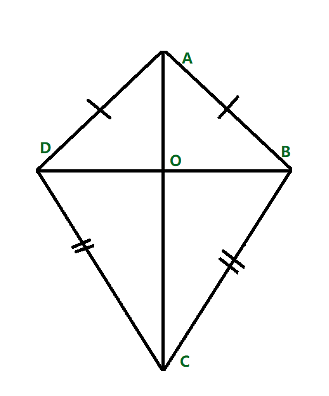
Perimeter of kite
The perimeter of the Kite Formula can be written as shown below:
| Kite perimeter = 2 (a + b) |
where a and b are two pairs of kites.
Also Read:- Geometry formula
Area of a kite
[Click Here for Sample Questions]
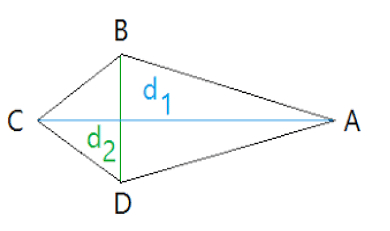
Area of kite
Area of a kite is given by the surface area covered within the boundaries of a kite. Area of the kite is calculated as half the product of its diagonals.
Suppose a kite has diagonals of length d1 and d2 units. Then the area of the kite is given by the formula,
| Area of kite= (d1 x d2)/2 |
Also Read: Area of rhombus
Properties of Kite
[Click Here for Sample Questions]
The following are the important properties of a kite:
- Kite has 2 diagonals that intersect each other at 90 degree angles.
- A kite is a quadrilateral.
- A kite is symmetrical about the main diagonal.
- Angles opposite to the main diagonal are equal.
- The kite can also be viewed as a pair of congruent triangles which have a common base.
Things to Remember
- A kite is a 2-dimensional geometric figure which consists of two pairs of triangles of equal size.
- The sum of all the sides of the kite is called the perimeter of a kite.
- Kite is also quadrilateral with two parallel sides of equal length. Hence perimeter of a kite is twice the sum of the length of two pairs of kite i.e 2(a+b)
- Area of a kite is given by: Area of kite= (d1 x d2)/2 in which d1 and d2 are the diagonals of the kite.
- The difference between a kite and a rhombus is that, all four sides of a rhombus are of equal length. Whereas, a kite has two adjacent sides of equal length.
- A kite can be formed by joining two congruent obtuse triangles joined by their base.
Solved Examples
Ques. Find the perimeter of the kite whose equal sides are 10 cm and 20 cm. [2 marks]
Ans. Given a=10cm and b=20cm
Kite perimeter = 2 (a + b)
=2 (10+20)
=2 (30)
Perimeter =60cm
Ques. A kite has its equal sides as 5 inches and 10 inches respectively. Find its perimeter. [2 marks]
Ans. Given a=5in. and b=15in.
Kite perimeter = 2 (a + b)
=2 (5+15)
=2 (20)
Perimeter = 40 inches
Ques. The sides of a kite are in the ratio of 2:5. If the side smaller among them is 20 inches, find its perimeter. [3 marks]
Ans. Given: a = 20 inch
a:b = 2:5
20:b = 2:5
b = 20 × (5/2)
b = 50 inches
Now, using the perimeter of a kite formula:
Perimeter = 2(a+b)
Perimeter = 2(20+50)
Perimeter = 2(70)
Perimeter = 140 inches
Ques. The sides of a kite are in the ratio of 7:8. If the side larger among them is 40 inches, find its perimeter. [4 marks]
Ans. Given: b = 40 inch
a:b = 7:8
a:40 = 7:8
a = 40 × (7/8)
b = 35 inches
Now, using the perimeter of a kite formula:
Perimeter = 2(a+b)
Perimeter = 2(40+35)
Perimeter = 2(75)
Perimeter = 150 inches
Ques. Find the perimeter of the following kite. [5 marks]

Ans. In order to find the length of the two shorter edges, use a Pythagorean triple:
3−4−5
3m−4m−5m
Use the Pythagorean theorem to find the length of larger side of kite:
A2+B2=C2
(9)2+(3)2=C2
C2=90
C=3√10m
The perimeter of a kite is given by:
P=2 (a+b)
P=2(5)+2(3√10)
P=10+6√10m
Ques. Find the perimeter of the following kite. [3 marks]
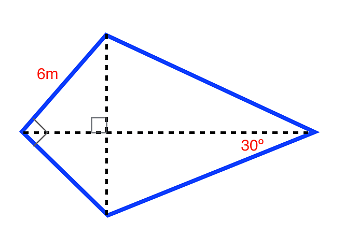
Ans. Use the formulas for a 45−45−90 triangle and a 30−60−90 triangle to find the lengths of the longer sides. The formula for a 45−45−90 triangle is a−a−a√2 and the formula for a 30−60−90 triangle is a−a√3−2a.
45−45−90 triangle is: 3√2−3√2−6
30−60−90 triangle is: 3√2−3√6−6√2
P=2(6√2m)+2(6)
P=12√2m+12m
Ques. The sides of a kite are in the ratio of 1:2. If the side smaller among them is 10 inches, find its perimeter. [4 marks]
Ans. Given: a = 10 inch
a:b = 1:2
10:b = 1:2
b = 10 × (2/5)
b = 4 inches
Now, using the perimeter of a kite formula:
Perimeter = 2(a+b)
= 2(10+4)
= 2(14)
Therefore, Perimeter of the kite = 28 inches
Ques. What is a kite? Is kite a quadrilateral? What is the perimeter of a kite? [5 marks]
Ans. A kite is a 2-dimensional figure consisting of two pairs of triangles of equal size. The sum of all the sides of the kite is called the kite perimeter.
In Euclidean Geometry, a kite is a quadrilateral with its four sides that can be joined into pairs of parallel lengths. In contrast, the parallelogram also has two pairs of sides that are equal in length, but opposite rather than parallel.
Perimeter of kite= 2(a+b)
Ques. List the difference between rhombus and kite. [3 marks]
Ans.
| Rhombus | Kite |
|---|---|
|
|
Ques. List the properties of a kite. [5 marks]
Ans. Properties of a kite are as follows:
- Kite has 2 diagonals that intersect each other at 90 degree angles.
- A kite is a quadrilateral.
- A kite is symmetrical about the main diagonal.
- Angles opposite to the main diagonal are equal.
- The kite can also be viewed as a pair of congruent triangles which have a common base.
Read Also:







Comments