Rhombus: Definition, Properties, Derivation & Solved Examples

Content Writer-SME

Rhombus is a form of quadrilateral which has four vertices and four edges and its two diagonals intersect each other at right angles. On the other hand, a quadrilateral is a type of polygon with 4 sides and 4 vertices enclosing 4 angles. The structure of a rhombus is diamond shaped, whose opposite sides are parallel and opposite angles are equal.

Thus, a rhombus can also be defined as a diamond-shaped quadrilateral.
In mathematics, rhombus-shaped geometry is commonly used in kites, diamond patterns, and crystals.
Area of rhombus formula is given as: \(Area = \frac{1}{2} (d_1\times d_2)\) where d₁and d₂ and length of diagonals.
It has four sides of equal length and two diagonals that bisect each other at right angles.
The perimeter of rhombus formula is given as: \(Perimeter = 4 \times side \space length\).

Table of Contents

What is a Rhombus?
Properties of Rhombus
Angles of Rhombus
Formulas Related to Rhombus
Solved Examples
Things to Remember
Sample Questions

Key Terms: Area, Perimeter, Angles, Quadrilateral, Polygon, Diagonal, Right Angles

What is a Rhombus?

[Click Here for Sample Questions]

A rhombus is a special type of quadrilateral whose diagonals intersect at right angles or 90 degrees. The following figure represents a rhombus ABCD with sides AB, BC, CD, and AD, and diagonals AC and BD that intersect each other at right angles.

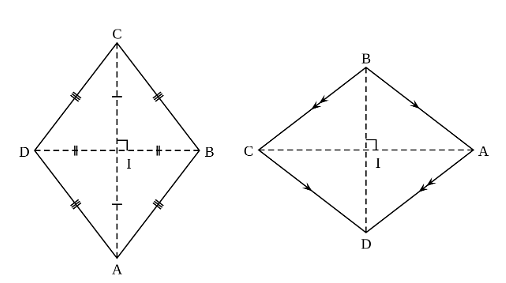
Rhombus

Rhombus Figure

In the above rhombus figure, all the four sides AB, BC, CD, and AD of the rhombus ABCD are equal while the sides AB and CD & AD and BC are parallel to each other. Thus the rhombus ABCD can also be called an equilateral quadrilateral due to its four sides being equal in length while it can also be called a special parallelogram because of the presence of two pairs of parallel sides.

Properties of Rhombus

[Click Here for Sample Questions]

A rhombus often appears in geometric shapes or playing cards, and may be depicted as a "tilted square" or diamond. Some of the properties of a rhombus are listed below:

Opposite angles of a rhombus are congruent or equal.
All the four sides of a rhombus are equal.
The two opposite sides of a rhombus are equal as well as parallel.
The two diagonals of a rhombus are perpendicular bisectors of each other.
The two diagonals of a rhombus bisect opposite angles.
The sum of any two adjacent or consecutive angles of a rhombus is 180°.
Joining the midpoint of the sides of a rhombus generates a rectangle.
Joining the midpoint of half the diagonals generates another rhombus.
A rhombus cannot have a circumscribing circle.
A rhombus cannot have an inscribing circle.

Important Facts about Rhombus

When the shorter diagonal of a rhombus is equal to one of its sides, two congruent equilateral triangles are generated.
When a rhombus is revolved on any of its side as the axis of rotation, a cylindrical surface with a convex cone at one end and concave cone at the other end are generated.
When a rhombus is revolved about the line joining the midpoints of the opposite sides as the axis of rotation, a cylindrical surface with two concave cones on both ends is generated.
When a rhombus is revolved about the longer diagonal as the axis of rotation, a solid having a maximum diameter equal to the shorter diagonal of the rhombus with two cones attached to their bases is generated.
When a rhombus is revolved about the shorter diagonal as the axis of rotation, a solid having a maximum diameter equal to the longer diagonal of the rhombus with two cones attached to their bases is generated.

Angles of Rhombus

[Click Here for Sample Questions]

Listed below are important facts related to rhombus angles:

A rhombus consists of four interior angles.
Sum of the interior angles of a rhombus add up to 360°.
The four opposite angles of a rhombus are equal to each other.
Adjacent angles of a rhombus are supplementary.
The two diagonals of a rhombus bisect each other at right angles.
The two diagonals of a rhombus bisect the opposite angles.

Formulas Related to Rhombus

[Click Here for Sample Questions]

The two main attributes governing a rhombus are area and perimeter. Mentioned below are the details:

Area of Rhombus

The area of a rhombus formula can be represented by the region covered by it in a two-dimensional plane. Thus the formula of area of a rhombus can be defined as the product of its diagonals divided by 2 and can be represented as:

\(Area \space of \space Rhombus = \frac{1}{2} (d_1\times d_2)\) in square units

where d1 and d2 are the two diagonals of a rhombus.

Area of Rhombus

Area of Rhombus

Derivation of Area of Rhombus Formula:

Let us consider the rhombus shown in the figure above, the diagonal ‘d1’ divides the rhombus into two congruent triangles. As the diagonals of a rhombus are perpendicular to each other, the area of the upper triangle can be determined by considering d1 as the base of the triangle and one half of the other diagonal ‘d2’ as the height. Thus area ‘A1’ of the upper triangle can be calculated as

A1 = ½ * base * height

= ½ * d₁ * ½ * d₂

= ¼ (d₁d₂)

Since the area of the rhombus is twice the area of the upper triangle, so

Area of a Rhombus = 2 * ¼ (d₁d₂)

= ½ * d₁ * d₂

Therefore,

\(Area \space of \space Rhombus = \frac{1}{2} \space(d_1\times d_2)\) in square units

Perimeter of Rhombus

The perimeter of a rhombus is defined as the total length of its boundaries. Or in other words, the perimeter of a rhombus is the sum of its four sides and can be expressed as

\(Perimeter \space of \space Rhombus = 4 \times side \space length\)

where ‘a’ represents each side of a rhombus.

Also Check: Perimeter Formula

Solved Examples

[Click Here for Sample Questions]

Example 1: A rhombus with diagonals of length 6cm and 12 cm respectively is given. Determine its area.

Solution: Given,

Diagonal d₁ = 6cm

Diagonal d₂= 12 cm

Since the area of a rhombus = (d₁ x d₂)/2 square units

= (6x12)/2

= 36 square cm

Example 2: Find the perimeter of a rhombus with sides of length equal to 5 cm.

Solution: Given,

Side of the rhombus = 5cm

Since all sides of a rhombus are equal in length,

Perimeter of a rhombus = 4 x side

= 4 x 5

= 20 cm

Example 3: Determine the diagonal of a rhombus with area 121 cm² and length of the longest diagonal is 22 cm.

Solution: Given,

Area of rhombus = 121 cm²

Length of diagonal d₁ = 22 cm

Since the area of a rhombus = (d₁ x d₂)/2 square units

121 = (22 x d₂)/2

121 = 11 x d₂

or 11 = d₂

So, the length of another diagonal is 11 cm.

Example 4: Determine the height of a rhombus whose area is 315 cm² and perimeter is 180 cm.

Solution: Given,

Perimeter of the rhombus = 180 cm

Since perimeter of a rhombus = 4 x side

Side of the rhombus = 180/4

= 45 cm

Since area of rhombus = b × h

⇒ 315 = 45 × h

⇒ h = 315/45

⇒ h =7 cm

So, the height of the rhombus is 7cm.

Things to Remember

Rhombus is a special type of quadrilateral whose diagonals intersect each other at right angles.
All the four sides of a rhombus have equal length.
The opposite sides of a rhombus are parallel while the opposite angles are equal in length.
A square can be called a rhombus while the reverse is not true.
The sum of two adjacent angles of a rhombus is equal to 180 degrees.
The area of a rhombus is equal to the product of its two diagonals divided by 2.
The perimeter of a rhombus is equal to the sum of all four sides.

Also Check: Area Formulas

Sample Questions

Ques. Can a square be considered a rhombus? (2 marks)

Ans. The primary criteria for any other quadrilateral to be treated as a rhombus is that all its four sides must be equal in length with the two diagonals being perpendicular to each other. Since a square has all its four sides equal in length, with its two diagonals perpendicular to each other and bisect the opposite angles just like a rhombus. In addition, just like a rhombus, squares also consist of 4 congruent sides. Thus a square can always be treated as a rhombus. But the reverse is not true, thus all rhombuses are not square.

Ques. Can a rhombus be considered a square? (2 marks)

Ans. Though all the sides of a square are equal, with the opposite sides being parallel and opposite angles are equal, all the angles in a rhombus are not equal to 90 degrees, its diagonals are not equal, the diagonals don’t bisect the angles to give 45 degree angles. In addition, a rhombus has 2 lines of symmetry instead of 4 lines of symmetry just like a square and has rotational symmetry of order 2 instead of order 4 like a square. Thus it can be concluded that though a rhombus has few properties similar to a rhombus it has few other properties which are dissimilar to a square. So a rhombus can never be considered a square.

Ques. Are all angles of a rhombus equal to 90 degrees? (2 marks)

Ans. No, all angles of a rhombus need not be necessarily equal to 90 degrees. Though the sum of two interior angles in a rhombus is equal to 180 degrees just like any other quadrilateral, only if a rhombus has all its four interior angles equal to 90-degree then the same rhombus can be considered as square.

Ques. Can a rhombus be considered a regular polygon? (3 marks)

Ans. No, a rhombus can never be considered a regular polygon. A regular polygon must possess the following properties:

It should be equiangular i.e. all the angles must be of equal measure.
It should be congruent or, equilateral i.e. all its sides should be of equal length.
But a rhombus is only equilateral with sides of equal length and opposite angles of equal measure. Thus a rhombus is an equilateral polygon and not an equiangular polygon and thus can never be considered a regular polygon.

Ques. What are the basic properties of a rhombus? (3 marks)

Ans. The basic properties of a rhombus are listed below:

The opposite angles of a rhombus are congruent.
The diagonals of a rhombus intersect each other at right angles.
The diagonals of a rhombus bisect the opposite interior angles.
The adjacent angles of a rhombus are supplementary to each other.

Ques. List down the differences between rhombus and parallelogram? (5 marks)

Ans. Differences between rhombus and parallelogram is listed below:

A rhombus is a two-dimensional figure with all its four sides being parallel to each other while a parallelogram is also a two-dimensional figure with only its opposite sides being parallel to each other.
A rhombus has all its four sides of equal length while a parallelogram has only its opposite sides of equal length.
Diagonals of a rhombus bisect each other at right angles forming two scalene triangles while diagonals of a parallelogram bisect each other forming congruent triangles.
Every rhombus is a parallelogram but the reverse is not true.

Ques. Determine the area of a rhombus with each side being of length 17 cm and length of one of the diagonals is 16 cm. (5 marks)

Ans. Let ABCD is a rhombus with sides AB, BC, CD, and DA being equal to 17 cm

The diagonal AC is of length 16 cm.

Then AO = 8 cm

In AOD,

AD² = AO² + OD²

⇒ 17² = 8² + OD²

⇒ 289 = 64 + OD²

⇒ 225 = OD²

⇒ OD = 15

So BD = 2 OD

= 2 × 15

= 30 cm

Since the area of a rhombus = (d₁x d₂)/2 square units

= 1/2 × 16 × 30

= 240 cm²

So, the area of the rhombus is 240 cm² .

Read Also:

Perimeter of Parallelogram	Laws of Vector Addition	Vector Formula
Remainder Theorem	Areas of Parallelograms and Triangles	Congruence of Triangles
Types of Quadrilaterals	Quadrilaterals	Types of Triangles
Difference Between Variance and Standard Deviation	Logarithm Formula	Geometry Formula

Rhombus: Definition, Properties, Derivation & Solved Examples

What is a Rhombus?

Properties of Rhombus

Important Facts about Rhombus

Angles of Rhombus

Formulas Related to Rhombus

Area of Rhombus

Perimeter of Rhombus

Solved Examples

Things to Remember

Sample Questions

CBSE X Related Questions

1.
In the adjoining figure, $\triangle CAB$ is a right triangle, right angled at A and $AD \perp BC$. Prove that $\triangle ADB \sim \triangle CDA$. Further, if $BC = 10$ cm and $CD = 2$ cm, find the length of AD.

2.
From one face of a solid cube of side 14 cm, the largest possible cone is carved out. Find the volume and surface area of the remaining solid.
Use $\pi = \dfrac{22}{7}, \sqrt{5} = 2.2$

4.
Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

5.
Prove that \(\dfrac{\sin \theta}{1 + \cos \theta} + \dfrac{1 + \cos \theta}{\sin \theta} = 2\csc \theta\)

6.
Let $p$, $q$ and $r$ be three distinct prime numbers. Check whether $pqr + q$ is a composite number or not. Further, give an example for three distinct primes $p$, $q$, $r$ such that
(i) $pqr + 1$ is a composite number
(ii) $pqr + 1$ is a prime number

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

Rhombus: Definition, Properties, Derivation & Solved Examples

What is a Rhombus?

Properties of Rhombus

Important Facts about Rhombus

Angles of Rhombus

Formulas Related to Rhombus

Area of Rhombus

Perimeter of Rhombus

Solved Examples

Things to Remember

Sample Questions

CBSE X Related Questions

1.In the adjoining figure, $\triangle CAB$ is a right triangle, right angled at A and $AD \perp BC$. Prove that $\triangle ADB \sim \triangle CDA$. Further, if $BC = 10$ cm and $CD = 2$ cm, find the length of AD.

2.From one face of a solid cube of side 14 cm, the largest possible cone is carved out. Find the volume and surface area of the remaining solid.Use $\pi = \dfrac{22}{7}, \sqrt{5} = 2.2$

4.Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

5.Prove that \(\dfrac{\sin \theta}{1 + \cos \theta} + \dfrac{1 + \cos \theta}{\sin \theta} = 2\csc \theta\)

6.Let $p$, $q$ and $r$ be three distinct prime numbers. Check whether $pqr + q$ is a composite number or not. Further, give an example for three distinct primes $p$, $q$, $r$ such that (i) $pqr + 1$ is a composite number (ii) $pqr + 1$ is a prime number

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

1.
In the adjoining figure, $\triangle CAB$ is a right triangle, right angled at A and $AD \perp BC$. Prove that $\triangle ADB \sim \triangle CDA$. Further, if $BC = 10$ cm and $CD = 2$ cm, find the length of AD.

2.
From one face of a solid cube of side 14 cm, the largest possible cone is carved out. Find the volume and surface area of the remaining solid.
Use $\pi = \dfrac{22}{7}, \sqrt{5} = 2.2$

4.
Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

5.
Prove that \(\dfrac{\sin \theta}{1 + \cos \theta} + \dfrac{1 + \cos \theta}{\sin \theta} = 2\csc \theta\)

6.
Let $p$, $q$ and $r$ be three distinct prime numbers. Check whether $pqr + q$ is a composite number or not. Further, give an example for three distinct primes $p$, $q$, $r$ such that
(i) $pqr + 1$ is a composite number
(ii) $pqr + 1$ is a prime number