
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Polygon is a flat two-dimensional structure that is formed of multiple line segments. The word “Polygon” is derived from the Greek words “poly” and “gonna” which translates to “many” and “angles” respectively. Therefore, a polygon is a shape with multiple angles. Polygon is formed of straight lines which are known as the sides of a polygon. Based on the number of its sides, a polygon can be classified as a triangle, quadrilateral, pentagon, hexagon, heptagon, octagon, nonagon, and decagon accordingly. In this article, we will have a look at the various types of polygons and look at their properties.
| Table of Contents |
Key Terms: Polygons, Quadrilateral, Triangle, Pentagon, Hexagon, Interior Angles, Isosceles Triangle, Equilateral, Equiangular
What are Polygons?
[Click Here for Sample Questions]
A polygon can be understood as a rectilinear shape that has three or more sides. It does not comprise a curved side. Three minimum line segments or sides are needed to make any closed figure. The vertex of a polygon refers to the points or corners where the two line segments or sides of polygons intersect each other. A polygon will have the same number of vertices and sides.

Polygons
The video below explains this:
Types of Polygons Detailed Video Explanation:
Read More: Frequency Polygons
Types of Polygon
[Click Here for Sample Questions]
On the basis of the sides and vertices of a polygon, they are further classified into many types as we will see below.
-
Equilateral Polygon
A polygon having all equal sides is known as an equilateral polygon. Example: Rhombus, Square, Equilateral Triangle.

Equilateral Polygon
-
Equiangular Polygon
A polygon with all angles equal is known as an equiangular polygon. Example: Square and Equilateral Triangle.
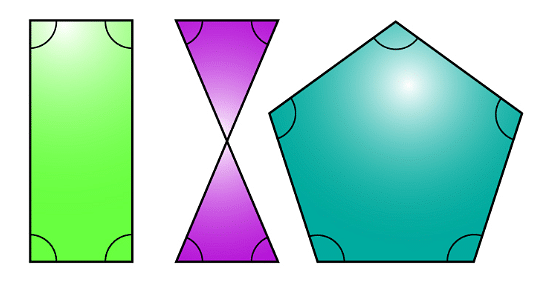
Equiangular Polygon
Also read:
Types of Polygon on the basis of their side length
According to their side length, polygons can be classified as:
-
Regular Polygon
A polygon having all sides of the same length is referred to as a regular polygon. A regular polygon is both equilateral and equiangular. For example, square and equilateral triangles.
-
Irregular Polygon
A polygon having variable side lengths is referred to as an irregular polygon. For example, Rhombus and Rectangle.

Regular and Irregular Polygons
Types of Polygon Based on Their Interior Angles
On the basis of their interior angles, polygons can be classified as:
-
Concave Polygon
A polygon having at least one of its angles more than 1800 is known as a concave polygon. When a concave polygon is extended, some sides of it go inside the polygon.
-
Convex Polygon
A polygon whose interior angles are less than a straight angle is known as a convex polygon. When a convex polygon is extended, none of its sides goes inside it and its vertices are always in an outward direction.
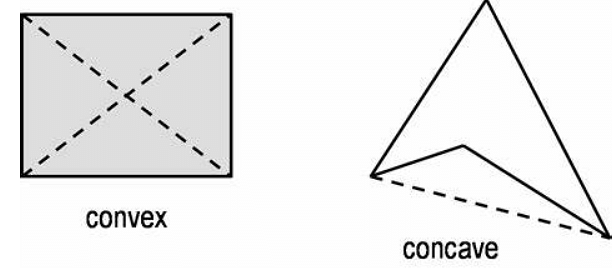
Convex and Concave Polygons
Read More: Pythagoras Theorem
Types of Polygon Based on the Number of Sides
The sides of a polygon are referred to as the straight lines that form these shapes. The corners at which these points meet are known as the vertex. The different types of polygon based on their number of sides are as given below:
-
Triangle
A polygon that has three sides is known as a triangle. All the interior angles of a triangle give a sum of 1800. Further, these triangles can be classified into various categories such as:
- Scalene Triangle: A triangle having all three sides of different lengths is a scalene triangle.
- Isosceles Triangle: A triangle having two equal sides and a side of different side lengths is an isosceles triangle.
- Equilateral Triangle: A triangle with all sides of equal length is known as an equilateral triangle.
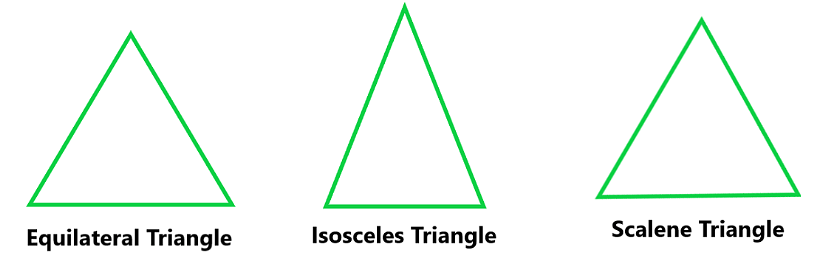
Types of Triangles
Also Read:
-
Quadrilateral
A four-sided polygon is referred to as a quadrilateral or a quadrangle. The various types of a quadrilateral polygon are rectangle, square, parallelogram, rhombus. The sum of all the interior angles of a polygon is 3600.

Quadrilateral
-
Pentagon
A polygon with 5 sides in the same plane is a pentagon. The sum of all the interior angles of a pentagon is 5400.
- If all the five sides of the polygon are of the same length, it is a regular pentagon.
- A polygon with different side lengths is an irregular pentagon.
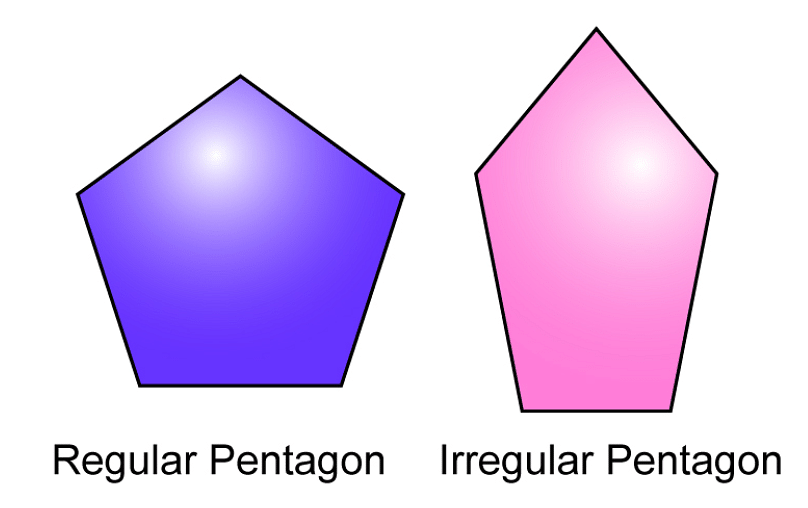
Regular and Irregular Pentagon
Also Read: Nature of Roots of Quadratic Equation
-
Hexagon
A polygon with 6 sides and 6 vertices is known as a hexagon. A regular hexagon is composed of all sides of equal lengths. The interior angles and exterior angles of a hexagon are also equal. The sum of all the interior angles of a hexagon equals 7200.
Also Read:
Types of Polygon with Sides 3 to 20
The various types of a polygon with sides 3 to 20 are as tabulated below:
| Name of the Polygon | Number of sides | Number of vertices | Angles |
|---|---|---|---|
| Triangle (Trigon) | 3 | 3 | 60o |
| Quadrilateral (four - gon) | 4 | 4 | 900 |
| Pentagon | 5 | 5 | 108o |
| Hexagon | 6 | 6 | 120° |
| Heptagon | 7 | 7 | 128.571° |
| Octagon | 8 | 8 | 135° |
| Nanogon | 9 | 9 | 140° |
| Decagon | 10 | 10 | 144° |
| Hendecagon | 11 | 11 | 147.27° |
| Dodecagon | 12 | 12 | 150o |
| Tridecagon | 13 | 13 | 152.3° |
| Tetradecagon | 14 | 14 | 154.28° |
| Petadecagon | 15 | 15 | 156° |
| Hexdecagon | 16 | 16 | 157.5° |
| Heptadecagon | 17 | 17 | 158.82° |
| Octadecagon | 18 | 18 | 160° |
| Enneadecagon | 19 | 19 | 161.05° |
| Icosagon | 20 | 20 | 162° |
| n-gon | n | n | (n-2)× 180° / n |
Polygon: Important Formulas
The important formulas of polygons are:
- To find the sum of all the interior angles of a given polygon having “n” slides = (n - 2) x 180o.
- To find the number of diagonals of a given polygon having “n” sides = (n-3)n/2
- To measure each of the interior angles of a regular polygon with “n” sides = (n-2)180o/n.
- The sum of all of the exterior angles of a polygon taken in order is equal to 3600.
- To measure each of the exterior angles of a regular polygon having n sides = 360o/n.
Also Read:
Things to Remember
- Polygon is a flat two-dimensional structure that is formed of multiple line segments.
- The vertex of a polygon refers to the points or corners where the two line segments or sides of polygons intersect each other.
- A polygon having all equal sides is known as an equilateral polygon while one with all angles equal is known as an equiangular polygon.
- A polygon having at least one of its angles more than 1800 is known as a concave polygon while a convex polygon has interior angles less than a straight angle.
- A polygon having three sides is known as a triangle.
- The various types of a quadrilateral polygon are rectangle, square, parallelogram, rhombus.
- Pentagon and hexagon are polygons with 5 and 6 sides respectively.
Sample Questions
Ques. Name the 10 types of polygons classified on the basis of the number of sides. (3 marks)
Ans. The 10 types of polygons on the basis of the number of sides they have are:
- Triangle with 3 sides.
- A quadrilateral with 4 sides.
- Pentagon with 5 sides.
- Hexagon with 6 sides.
- Heptagon with 7 sides.
- Octagon with 8 sides.
- Nonagon with 9 sides.
- Decagon with 10 sides.
- Hendecagon with 11 sides.
- Dodecagon with 12 sides.
Ques. If the given sum of all the interior angles of a Polygon is 3240o, how many sides does the polygon have? (3 marks)
Ans. As we know, the formula to find the sum of all interior angles of a given Polygon having ‘n’ sides = (n–2)180o.
⇒ 3240o = (n–2)180o
⇒ (n–2) = 3240o/180o = 18
⇒ (n–2) = 18
⇒ n = 18 + 2
⇒ n = 20
Therefore, the given Polygon has 20 sides.
Ques. In a given triangle ABC, the height of the triangle is represented by h and it is equal to 10 cm. The base of the triangle has a value of 5 cm. Find out the area of the triangle using the formula. (3 marks)
Ans. Given: Base = 5 cm
Height = 10 cm
Now, we know that:
Area of the triangle = ½ x base x height
Area = ½ x 5 x 10 = 25 cm
Therefore, the area of a triangle is 25 cm.
Ques. Find out the interior angle of a given regular Polygon having 12 sides. (3 marks)
Ans. We are given that the number of sides of the polygon, n = 12
The formula used to measure all the interior angles of a regular polygon having n sides = ((n–2) 180o)/n
Now, if we substitute the values in the given formula, we will get,
The interior angle of the given Polygon = ((12–2) 180o)/12
The interior angle of the given Polygon = (10×180o)/12
= 150o
Therefore, the interior angle of the given regular polygon is equal to 150o.
Ques. State some properties of a polygon. (3 marks)
Ans. The properties of a polygon are as stated below:
- For a regular polygon having n sides, each exterior angle is measured by the formula: 360o/n.
- Each of the interior angles of a regular n-sided polygon is measured as [(n – 2) × 180°]/n.
- For a polygon with n sides, the sum of all of its interior angles is equal to (n – 2) × 180°.
- The number of triangles that are formed through the joining of the diagonals from a corner of a given polygon is given as n - 2.
- A given polygon with n sides has n (n – 3)/2 number of diagonals.
Ques. What are the interior and exterior angles of a polygon? (5 marks)
Ans. A polygon has two types of angles which are as given below:
- Interior Angle
The interior angle of a polygon is the angle that exists on the inside of a shape or on the inside of the polygon. The sum of all of the interior angles of a polygon is given as:
The sum of all the interior angles of a polygon = (n – 2) x 180,
Here, n refers to the total number of sides that a polygon has
or it can also be given as:
Interior Angle = 180° – Exterior Angle,
or in radian, we can demonstrate it as,
Interior angle sum= (n – 2) x π radian
- Exterior Angle
The angles that are formed by a side of a polygon and an extension of the adjacent side are known as exterior angles. The sum of all the exterior angles of a given polygon is equal to 360o. The exterior angle can be determined by
Exterior Angle = 180° – Interior Angle
If the given polygon has n sides, then we can say that
The sum of all the exterior angles = n x 180° – the sum of all the interior angles
Ques. Find all the interior angles of a regular decagon. (5 marks)
Ans. We know that a decagon has ten sides.
Now, using the angle sum formula,
S = (n − 2) × 180°
We are given n = 10
Therefore,
Sum of all the angles of a given decagon = (10 − 2) × 180°
= 8 × 180°
= 1440°
Now, we know that a regular decagon has an equal interior angle.
Therefore, the measure of each of the interior angles of regular decagon = sum of all the interior angles/number of sides of the polygon
Interior angle = 1440 / 10
= 144°
Therefore, we get that the sum of the Interior Angle of a regular decagon is 1440° while each interior angle is 144°.
Ques. Explain the four main types of the polygon. (5 marks)
Ans. The four main types of polygons are:
- Regular Polygon: If all sides and the interior angles of a given polygon are equal or if we know that a polygon is equilateral and equiangular, then the polygon is called a regular polygon. For example rhombus, square, equilateral triangle, etc.
- Irregular Polygon: If all the given sides and interior angles of a polygon have a different measure, then that polygon is known as an irregular polygon. For example kite, scalene triangle, rectangle, etc.
- Convex Polygon: A polygon is known as a convex polygon if all the interior angles of a polygon are measured to be less than 180° or if a line segment exists between two points on the boundary of the polygon does not go outside it.
- Concave Polygon: A polygon is known as a concave polygon if one or more of the interior angles of a polygon is measured to be more than 180 degrees or if the polygon consists of at least one reflex interior angle. The concave polygon can at least have four sides.
Ques. What is a triangle? Explain the various types of triangles. (5 marks)
Ans. A triangle is a type of polygon that is formed through 3 line segments that intersect each other in a way that the triangle has three edges, three vertices, and three angles. On the basis of the angles and sides of a triangle, they are further classified into various types.
Triangle has the following properties:
- The area of the Triangle is measured by the formula - ½ × base × height
- The sum of all of the interior angles of a given triangle is 180o.
- The largest side of the triangle is the side opposite to the largest angle of this polygon.
- The perimeter of a triangle can be measured as the sum of lengths of all three given sides of a triangle.
The triangles can be classified as:
On the basis of sides of a triangle
Based on the sides, a triangle can be classified as:
- Scalene Triangle: A triangle having all three sides of different lengths is a scalene triangle.
- Isosceles Triangle: A triangle having two equal sides and a side of different side lengths is an isosceles triangle.
- Equilateral Triangle: A triangle with all sides of equal length is known as an equilateral triangle.
On the basis of the angle
Based on the angles, a triangle can be classified as:
- Acute Angled Triangle: A triangle with all of its angles as less than 90° is known as an acute angle triangle.
- Right Angled Triangle: If any one of the three angles of a given triangle is equal to 90°, then this type of triangle is referred to as a right-angle triangle.
- Obtuse Angled Triangle: If any one of the angles of a triangle is more than 90°, then this type of triangle is called an obtuse angle triangle.
Ques. If the sum of all the interior angles of a given polygon is 6, calculate how many sides does the polygon has? (5 marks)
Ans. Now, as we know the formula used in order to find the sum of interior angles of a polygon having n sides is,
= (n–2) straight angles
⇒ (n–2) = 6
⇒ n = 6 + 2
⇒ n = 8
Therefore, we get that the given polygon has 8 sides.
Ques. We have a quadrilateral ABCD, the side BD of the quadrilateral is 15 cm and the height of the 2 triangles ABD and BCD are 5 cm and 7 cm respectively. Calculate the area of the quadrilateral ABCD. (5 marks)
Ans. Diagonal of the triangle BD = 15 cm2
Now, we are given that the heights:
H1 = 5 cm and
H2 = 7 cm
The sum of the heights of two given triangles of the quadrilateral are = 5 + 7
= 12 cm
Therefore, the area of a quadrilateral = ½ x diagonal x sum of the heights of given two triangles
= ½ x (15 x 12) = 90 cm2
Therefore, we get the area of the quadrilateral as 90 cm2
Also Read:







Comments