Angles of a Parallelogram: Properties, Theorems & Proofs

Parallelogram is a quadrilateral with two pairs of parallel sides. In total, it has 4 vertices, 4 angles, and 4 sides. The 4 interior angles add up to a total of 360°, and consecutive angles add up to 180°. The opposite angles of a parallelogram are equal. The diagonals of the parallelogram cross each other but not at right angles and are not equal as well. 

Key takeaways: Parallelogram, Polygon, Angles, Sides, Diagonals, Congruence.

---

Properties of Angles of Parallelogram

[Click Here for Sample Questions]

Parallelogram is a polygon with 4 sides, which makes it a quadrilateral. Its distinct feature is that opposite sides are equal in length and are parallel to each other. One diagonal divides it into two congruent triangles, and its diagonals bisect each other. There are other factors about its angles that both set it apart from and it shares with other quadrilaterals, which are as follows:

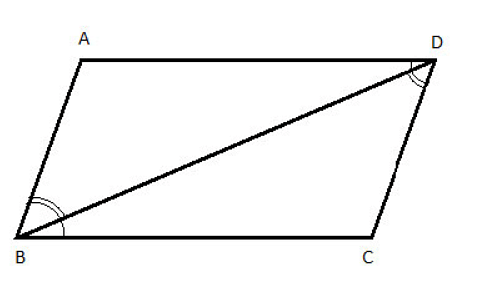
Parallelogram

Property 1: The opposite angles of a parallelogram are congruent, which means that they’re equal. So here, ∠A = ∠C, and ∠B = ∠D. 

Property 2: All 4 interior angles of a parallelogram add up to 360 degrees. So, ∠A + ∠B + ∠C + ∠D = 360 degrees.

Property 3: Consecutive angles in a parallelogram are supplementary, which means that they add up to 180 degrees. So, ∠A + ∠B = 180 degrees, ∠B + ∠C = 180 degrees, ∠C + ∠D = 180 degrees, and ∠D + ∠A = 180 degrees.

Read More:

---

Theorems & Proofs

[Click Here for Sample Questions]

Proofs and theorems help us better understand the various properties of parallelograms, which will make it easier to solve questions relating to them. Three theorems that are specific to angles in parallelograms are:

• Opposite angles are congruent
• If a quadrilateral has two opposite angles that are equal, then it’s a parallelogram
• Consecutive angles are supplementary

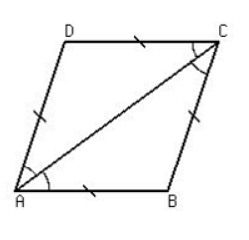
We can prove these theorems by drawing a diagonal across a parallelogram. A diagonal is a straight line that connects two opposite corners of certain shapes. Here's what it looks like in a parallelogram: 

Diagonal of a Parallelogram

There are formulas that use a parallelogram’s diagonals to solve problems, which can be found here.

Also Read: Angle Sum Property of Quadrilateral

Now, let’s prove those two theorems.

Theorem 1: Opposite angles are Congruent.

Proof: The diagonal AC divides parallelogram ABCD into triangles ADC and ABC. If we superimpose those triangles together, we can see that:

• AC is a common side for both triangles, hence equal. 
• By the law of alternate interior angles, ∠DCA = ∠CAB and ∠BCA = ∠CAD. 

Based on the congruence of triangles, these two points prove that triangles ADC and ABC are congruent. This makes ∠CBA = ∠CDA, because they are corresponding parts of congruent triangles.

We can also conclude that ∠DAB and ∠DCB are equal because we know the values of those angles split in half - and the sums would naturally also be the same.

This proves our theorem that opposite angles in parallelograms are always equal.

Also Read:

Theorem 2: Every quadrilateral with equal opposite angles is a parallelogram.

Proof: We’re given that the opposite angles are equal, so ∠A = ∠C and ∠D = ∠B. We also know that the sum of interior angles in a quadrilateral is 360 degrees, which would be the case here too. So, with the information we have, we can conclude that:

∠A + ∠B + ∠C + ∠D = 360

Since ∠A and ∠C are the same, and ∠D and ∠B are the same, we can rewrite this equation as:

2(∠A+∠D) = 360; divide this whole equation by two and we get:

∠A + ∠D = 180

This proves that the consecutive angles are supplementary. Therefore, AD is parallel to BC and AB is parallel to DC. That makes it 2 pairs of parallel sides in a quadrilateral, which means that it’s a parallelogram.

Also Read:

Theorem 3: Angles beside each other on a parallelogram are supplementary.

Proof: We’re given that AB and CD are parallel to each other, and it is clear that AD is a transversal across those two lines. By one of the rules of transversals, interior angles beside each other on a transversal add up to 180 degrees, so 4 and 5 in the diagram below are equal. Referring this to the parallelogram given above, this means that:

∠A + ∠D = 180

∠A + ∠B = 180

∠B + ∠C = 180

∠C + ∠D = 180

This proves that supplementary angles in a parallelogram add up to 180 degrees.

Also Read:

---

Things to Remember

[Click Here for Sample Questions]

• All parallelograms have equal opposite angles and supplementary consecutive ones.
• The interior angles of parallelograms, like all other quadrilaterals, add up to 360 degrees.
• There are ways to prove these theorems with the help of laws from topics such as congruency, and transversals.

Also Read:

---