
Collegedunia Team Content Curator
Content Curator
Polynomials are the algebraic expressions that contain variables, constants and exponents. The term polynomial is derived from the Greek words Poly and Nominal. Poly means many and the word nominal means terms. So, we can say that the expression having many terms is called a polynomial expression.
Read More: Degree of polynomial
| Table of Contents |
Keyterms: Polynomials, algebraic expression, variables, constants, exponents, Monomial, Binomial
What are Polynomials?
[Click Here for Sample Questions]
A polynomial is a mathematical equation containing variables, constants and exponents. In polynomials, the exponent on the variable is a whole number.
A polynomial consists of:
- Constants- A constant is a number whose value does not change in an expression. Constants are also referred to as the coefficients. (For Example- 2, -34, ½, etc.)
- Variables- A variable represents a number and its value varies when it is used in an expression. (For Example- x, y, z, etc.)
- Exponents- The exponent on a number or variable defines how many times it is used in the expression. (For Example- 2 in x2)
A polynomial consists of these 3 components combined using addition, subtraction, multiplication and division. But a polynomial can not have a variable as a divisor i.e. 5/x, 2/x+1, etc. are not polynomials.
The video below explains this:
Polynomials Detailed Video Explanation:
Read More: Polynomials Formulas
Degree of a Polynomial
[Click Here for Sample Questions]
- Degree of a polynomial with a single variable-
In a polynomial with a single variable, the degree is the largest exponent of the variable.
Ex: In the polynomial expression- x2 + 2x5 – x
The degree is 5
- Degree of a polynomial with multiple variables-
In a polynomial with multiple variables, each of the terms must be considered separately, and the degree is derived by adding the exponents of each variable in the polynomial.
Example: In 5xy2-3x+5y2-7
Considering the terms separately,
5xy2 has a degree of 3= 2+1
3x has a degree of 1
5y2 has a degree of 2
7 has a degree of 0
So, the degree of the polynomial is equal to the degree of the term 5xy2, i.e., 3.
In other words, Let P(y) be a polynomial in y, then the highest power of y in the P(y) will be the degree of polynomial P(y).
Read More: Roots of Polynomials
Types of Polynomial
[Click Here for Sample Questions]
The polynomials are classified on two basis-
- Number of Terms.
- Degree of Variables
-
Number of Terms-
The type of the polynomial depending on the number of terms are-
- a) Monomial – A polynomial in which a single term is used.
Example: 2x, 5y2, 16x2y
- b) Binomial – A polynomial in which two terms are used.
Example: 4x2+x3, 5x+4, 3x2+2y
- c) Trinomial – A polynomial in which three terms are used.
Example: x2+3x+4
-
Degree of Variables-
On the basis of degree of the variables, the polynomials are divided in the following way:
| Type of polynomial | Degree | Form |
|---|---|---|
| Constant | 0 | P(x) = a |
| Linear | 1 | P(x) = ax + b |
| Quadratic | 2 | P(x) = ax2 + ax + b |
| Cubic | 3 | P(x) = ax3 + ax2 + ax + b |
| Bi-quadratic | 4 | P(x) = ax4 + ax3 + ax2 + ax + b |
Value of a Polynomial
[Click Here for Sample Questions]
Let p(y) is a polynomial in y and α could be any real number,
then the value calculated after putting the value y = α in p(y) is the final value of p(y) at y = α. This shows that p(y) at y = α is represented by p (α).
For example:
Let a polynomial p(x) = x2 – 3x – 4.
Then, putting x = 2 in the polynomial, we get p(2) = 22 – 3 × 2 – 4 = – 6.
The value ‘– 6’ is obtained by replacing x by 2 in x2 – 3x – 4, is the value of x2 – 3x – 4 at x = 2.
Read More: Geometric Progression (G. P.)
Graphical Representation
[Click Here for Sample Questions]
The equation y = x, on a graph, will always be a straight line that joins all the points which have their x coordinate equal to their y coordinate. Example – (5,5), (-3,3) , etc.
Graphical Representation of a Linear Polynomial:
The graph of a linear polynomial is always a straight line that cuts the X-axis at exactly one point.

Graphical Representation of a Linear Polynomial
Graphical Representation of a Quadratic Polynomial:
- When the graph cuts the x-axis at the two points then these two points are the two zeroes of that quadratic polynomial.
- When the graph cuts the x-axis at only one point then that particular point is the zero of that quadratic polynomial and the equation is in the form of a perfect square
- When the graph does not intersect the x-axis at any point i.e. the graph is either completely above the x-axis or below the x-axis then that quadratic polynomial has no zero as it is not intersecting the x-axis at any point.
- The graph of a quadratic equation is always a parabola. It is like a U-shape either in upward or downward directions, depending on the equation.
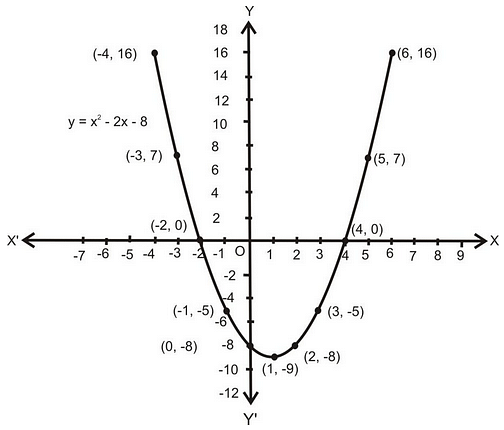
Graphical Representation of a Quadratic Polynomial
Zero of the Polynomial
[Click Here for Sample Questions]
A zero of the polynomial p(x) is the value of x for which the value of p(x)= 0.
For Example-
In an expression x2 – 3x – 4, p(0) is the value of p(x) at x = 0, which is – 4. This is called the zero of the polynomial.
Geometrical Meaning of the Zeroes of a Polynomial:
Plotting a zero polynomial (whose value is zero) on a graph, results in a parabola, which might appear at different points, representing the different cases-
- One parabola may cut the x-axis and y-axis at two points
- One parabola may cut the x-axis and y-axis at a single point
- The parabola may end up entirely one side of the x-axis
- The parabola may end up entirely on one side of the y-axis.

Geometrical Meaning of the Zeroes of a Polynomial
- First graph shows that the linear equation has only one zero.
- Second graph shows that the linear equation has two zeroes.
- Third graph shows that the linear equation has three zeroes.
Read More: Zeros of Polynomial
Relationship between the Zeroes and Coefficients of a Polynomial:
For factorising a quadratic polynomial, it has to be split into multiple factors, then taking a common term to obtain the result. The two remaining terms can be treated as factors.
Example: To factorise the polynomial, 3x2+14x+8,
Split the equation into four terms without changing their values:
3x2+2x+12x+8=0
Then taking the common and splitting it into factors:
(3x+2)(x+4)=0
Hence, the factors are: -2/3 and -4.
Also Read:
| Related Articles | ||
|---|---|---|
| Complex Numbers and Quadratic Equations | Geometric Mean (G.M.) | Bayes Theorem Formula |
| Sequence and Series | Arithmetic Progressions Revision Notes | Real Numbers Formula |
Division Algorithm
[Click Here for Sample Questions]
If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then the division algorithm can be expressed as-
p(x) = g(x) × q(x) + r(x)
(Dividend = Divisor x Quotient + Remainder)
Where,
p(x)= Dividend
g(x)= Divisor
q(x)= Quotient
r(x)= Remainder
Read More: Pair of Linear Equations in Two Variables Important Questions
Sample Questions
Ques. 1: If the sum of the zeroes of the polynomial p(x) = (k2 – 14) x2 – 2x – 12 is 1, then find the value of k. (4 marks)
Ans: p(x) = (k2 – 14) x2 – 2x – 12
Here a = k2 – 14, b = -2, c = -12
Sum of the zeroes, (α + β) = 1 …[Given]
⇒ −ba = 1
⇒ −(−2)k2 −14 = 1
⇒ k2 – 14 = 2
⇒ k2 = 16
⇒ k = ±4
Ques.2 : Find the zeroes of the quadratic polynomial x2 + 7x + 10, and verify the relationship between the zeroes and the coefficients. (4 marks)
Ans: We have x2 + 7x + 10 = (x + 2)(x + 5)
So, the value of x2 + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0,
i.e., when x = – 2 or x = –5.
Therefore, the zeroes of x2 + 7x + 10 are – 2 and – 5.
Now
sum of zeroes = -2+ (-5) = -(7) = -(7)/1
product of zeroes= (-2) x (-5) = 10 =10/1
Ques.3: Find a quadratic polynomial, the sum and product of whose zeroes are – 3 and 2, respectively. (4 marks)
Ans: Let the quadratic polynomial be ax2 + bx + c, and its zeroes be α and β.
We have α + β = – 3 = b/a,
and αβ = 2 = c/a.
If a = 1, then b = 3 and c = 2.
So, one quadratic polynomial which fits the given conditions is x2 + 3x + 2.
We can check that any other quadratic polynomial that fits these conditions will be of the form
k(x2 + 3x + 2), where k is real.
Ques.4: Divide 3x3 + x2 + 2x + 5 by 1 + 2x + x2. (4 marks)
Ans: We first arrange the terms of the dividend and the divisor in the decreasing order of their degrees. Arranging the terms in this order is called writing the polynomials in standard form. Here, the dividend is already in standard form, and the divisor, in standard form, is x2 + 2x + 1.
Step 1 : To obtain the first term of the quotient, divide the highest degree term of the dividend (i.e., 3x3 ) by the highest degree term of the divisor (i.e., x2 ). This is 3x. Then carry out the division process. What remains is – 5x2 – x + 5.
Step 2: Now, to obtain the second term of the quotient, divide the highest degree term of the new dividend (i.e., –5x2) by the highest degree term of the divisor (i.e., x2). This gives –5.
Again, carry out the division process with –5x2 – x + 5.
Step 3: What remains is 9x + 10. Now, the degree of 9x + 10 is less than the degree of the divisor
x2 + 2x + 1. So, we cannot continue the division any further.
So, the quotient is 3x – 5 and the remainder is 9x + 10.
Also,
(x2 + 2x + 1) × (3x – 5) + (9x + 10) = 3x3 + 62 + 3x – 5x2 – 10x – 5 + 9x + 10 = 3x3 + x2 + 2x + 5
Ques.5: Find the condition that zeros of polynomial p(x) = ax2 + bx + c are reciprocal of each other. (4 marks)
Ans: Let α and 1/α be the zeroes of P(x).
P(a) = ax2 + bx + c …(given)
Product of zeroes = c
⇒ α × 1/α = c
⇒ 1 = c
⇒ a = c
Coefficient of x2 = Constant term
Ques.6: If the zeroes of the polynomial x2 + px + q are double in value to the zeros of 2x2 – 5x – 3, find the value of p and q. (5 marks)
Ans: We have, 2x2 – 5x – 3 = 0
= 2x2 – 6x + x – 3
= 2x(x – 3) + 1(x – 3)
= (x – 3) (2x + 1)
Zeroes are:
x – 3 = 0 or 2x + 1 = 0
⇒ x = 3 or x = /2
Since the zeroes of the required polynomial are double of the given polynomial.
Zeroes of the required polynomial are:
3 × 2, (−1/2 × 2), i.e., 6, -1
Sum of zeroes, S = 6 + (-1) = 5
Product of zeroes, P = 6 × (-1) = -6
Quadratic polynomial is x2 – Sx + P
⇒ x2 – 5x – 6 …(i)
Comparing (i) with x2 + px + q
p = -5, q = -6
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Check:






Comments