Polynomials in One Variable: Types & Degree of Polynomial

Content Curator

Polynomial is a kind of algebraic expression about one or more than one term with a non-zero coefficient. Any algebraic expressions with only one variable in them are known as ‘polynomials in one variable. The polynomial expression consists of coefficients, constants, and variables. The word "polynomial" is derived from two root words, namely, “poly" and “nomials”. "Poly" means many, and "nomials" means names or terms.

Table of Content

What are Polynomials in One Variable?
Polynomials Important Terms
Degree of a Polynomial
Types of Polynomial
Things to Remember
Sample Questions

Read More: Degree of a Polynomial

Key Takeaways: polynomials, degree of polynomial, zero polynomial, linear polynomial, cubic polynomial, quadratic polynomial.

What are Polynomials in One Variable?

[Click Here for Sample Questions]

Any algebraic expressions with only one variable in them are known as ‘polynomials in one variable.’ Here ‘n’ is a non-negative, positive, or zero integer. It is a real number called the coefficient of the term.

Examples:

x+2
x² + 5x + 2
p³ + 2p² - p
q⁴ – 3q² + 7q − 5

Polynomials in One Variable

Polynomials in One Variable

The video below explains this:

Polynomials Detailed Video Explanation:

Also Read:

Polynomials	Polynomials Formulas
Roots of polynomials	Degree of polynomials

Polynomials – Important Terms

[Click Here for Sample Questions]

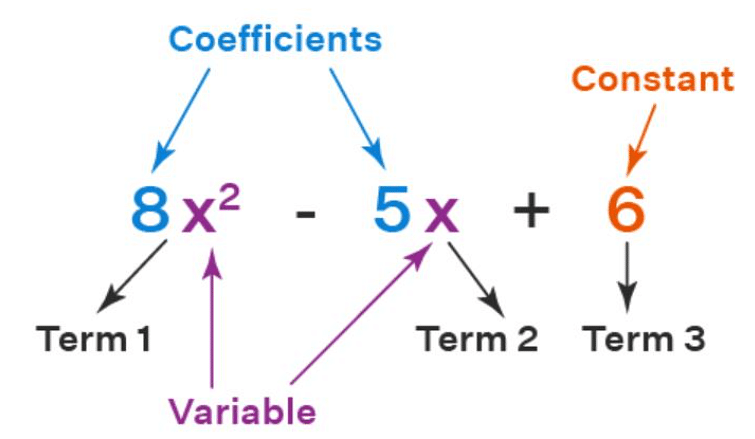
All Polynomial equations consist of the following terms which should be familiarized.

Term: A variable, constant, or a product of variable, and constant is called a term.
Coefficient: Any numerical value written along with a variable is called a coefficient.
Variable: Any letter that denotes the unknown value in an expression is called a variable.
Constant: Any number whose value never changes in an expression is called a constant.

Example to show the relation between different terms in polynomials:

If Polynomial = 3x+1

Variable → x

Coefficient → 3

Constant → 1

Terms → 3x and 1

Degree of a Polynomial

[Click Here for Sample Questions]

The degree of a polynomial is the highest power of the variable in it.

For example, 7x² + 2x + 5

The degree of a polynomial is 2, as the highest power of the variable “x” in this polynomial is 2.

Degree of Polynomial

Degree of Polynomial

Also Read:

Zeros of Polynomial	Roots of Polynomial	Degree of Polynomial

Types of Polynomial

[Click Here for Sample Questions]

The different types of polynomials are as follows.

Zero Polynomial or Constant Polynomial
Linear Polynomial
Quadratic Polynomial
Cubic Polynomial

Zero Polynomial

Polynomial with its degree as zero is called zero polynomial or constant polynomial. These polynomials have only constants, but not variables. These polynomials have constant terms with no variable. 5, which we can also write as 5x0, is an example of zero polynomial.

2, 5, 7 are examples of zero or constant polynomials. They can be written as

2x⁰, 5x⁰, 7x⁰and so on.

Zero Polynomial

Zero Polynomial

Linear Polynomial

Polynomial with the degree of 1 is called a linear polynomial. The linear polynomial with one variable has one solution.

Examples:

q+2
x+5
y+12
3p-27

Linear Polynomial

Linear Polynomial

Quadratic Polynomial

Polynomial with the highest degree of 2 is the quadratic polynomial. A quadratic polynomial has one variable and consists of two solutions.

Examples:

8x² – 12
x² +10x+8
n²+18
y² + 5y + 10
3m² − 8m + 18

Quadratic Polynomial

Quadratic Polynomial

Read More: Polynomials Revision Notes

Cubic Polynomial

Polynomial with the highest degree of 3 is called the cubic polynomial. A cubic polynomial consists of 3 solutions.

Examples:

5x³– 15
4x³- 9x² + 3x + 8
12q³ + (8/2) - 5y³ − 9
x3 + 8x² − 9x – 3

Cubic Polynomial

Cubic Polynomial

Things to Remember

[Click Here for Sample Questions]

Polynomial is a kind of algebraic expression about one or more than one term with a non-zero coefficient.
The polynomial expression consists of coefficients, constants, and variables.
The polynomial with its degree as zero (0) is called zero polynomial or constant polynomial.
The polynomial with the degree of 1 (one) is called a linear polynomial.
The polynomial with the highest degree of 2 is the quadratic polynomial.
The polynomial with the highest degree of 3 is called the cubic polynomial.

Also Read:

Real-Valued Function	Trigonometric Functions	Complex numbers and Quadratic Equations

Sample Questions

Ques: How many types of polynomials are there? What are they? (1 mark)

Ans: Polynomials are primarily four types. They are monomials, binomials, and trinomials. A monomial is a polynomial with one term. A binomial is a polynomial with two terms. A trinomial is a polynomial with three terms.

Ques: Can polynomials have square roots? Give your explanation. (2 marks)

Ans: No. Generally a polynomial term must not contain square roots of variables, fractional or negative powers on the variables, and variables in the denominators of any fractions.

Ques: What are polynomials in one variable? Give examples (5 marks)

Ans: Examples of a polynomial with one variable are as follows

Polynomial	Degree	Example
Zero Polynomial	0	2 x0
Linear Polynomial	1	x + 5
Quadratic Polynomial	2	3m2 − 8m + 18
Cubic Polynomial	3	6x³-9x²+3x+8

Ques: Can a polynomial have two variables? (1 mark)

Ans: Yes, a polynomial can have more than one variable. It can be expressed in the same way as polynomials with one variable.

Ques: What are the different uses of polynomials? (5 marks)

Ans:

Polynomials form an important part of the mathematical language and an important part of algebraic expressions.
They are useful to express numbers as a result of mathematical operations.
They are "building blocks" of rational expressions.
Polynomials are used to determine the composition of different compounds and molecules.
In statistical formulas polynomials are used to ascertain values of animal birth and death rates, demographic trends, and monetary flow.

Ques: What is a polynomial? Is a polynomial a cubic polynomial? (2 marks)

Ans: A polynomial is an algebraic expression with constants and variables with exponents as whole numbers. Yes, a polynomial can be cubic. The cubic polynomial is a polynomial with the highest power of the degree is 3.

Ques. Is the function zero a polynomial? (2 marks)

Ans. The value 0 can be thought of as a (constant) polynomial, known as the zero polynomial, just like any other constant value. It has no nonzero terms and hence, technically speaking, no degree. As a result, its degree is frequently unclear.

Ques. How many zeros does the polynomial have? (2 marks)

Ans. A polynomial function can have 0 zeros, 1 zero, or many zeros. Positive, odd-order polynomial functions must have at least one zero, but positive, even-order polynomial functions may or may not contain a zero. Any polynomial of positive order, whether odd or even, can have a maximum number of zeros equal to its order.

Ques. Find a quadratic polynomial, the sum and product of whose zeroes are 0 and -√2 respectively. (CBSE 2015) (2 marks)

Ans. Quadratic polynomial is

x² – (Sum of zeroes) x + (Product of zeroes)

= x² – (0)x + (-√2)

= x² – √2

Ques. If the zeroes of the polynomial x² + px + q are double in value to the zeroes of 2x² – 5x – 3, find the value of p and q. (CBSE 2012) (3 marks)

Ans. We have, 2x² – 5x – 3 = 0

= 2x² – 6x + x – 3

= 2x(x – 3) + 1(x – 3)

= (x – 3) (2x + 1)

Zeroes are:

x – 3 = 0 or 2x + 1 = 0

⇒ x = 3 or x = −1/2

Since the zeroes of the required polynomial are double of a given polynomial.

Zeroes of the required polynomial are:

3 × 2, (−1/2 × 2), i.e., 6, -1

Sum of zeroes, S = 6 + (-1) = 5

Product of zeroes, P = 6 × (-1) = -6

Quadratic polynomial is x² – Sx + P

⇒ x² – 5x – 6 …(i)

Comparing (i) with x² + px + q

p = -5, q = -6

Also Read:

Straight Lines	Angle Between Two Lines
Horizontal and Vertical Lines	Conic Sections

Polynomials in One Variable: Types & Degree of Polynomial