Events in Probability: Definition, Types, Examples

Probability is a crucial branch of mathematics which deals mainly with how likely it is for an event to occur. It is indicated by higher and lower. Higher probability of something means there are more chances for it to happen. On the other hand, if some event has lower probability, it denotes that it is very less likely to take place. 

There are two main aspects of probability, 0 and 1. 0 indicates the impossibility of an event, whereas 1 implies that there is surety it can happen. The concept of probability has enormous reach in various fields in the world. It was introduced by two famous French mathematicians, Blaise Pascal and Pierre de Fermat.

Probability Events: Common Terms

Before we move on to studying the different types of events, it is important that we familiarise ourselves with some common terms. 

Sample Space - Sample space refers to all the outcomes of an experiment which are possible to happen. It is denoted by the letter S. For example an unbiased dice is thrown. Its sample space will be, S = {1, 2, 3, 4, 5, 6}

Sample Points - Each outcome in the sample space is known as a sample point. These are also called elements. For example, I throw an unbiased dice. I can say that there are a total of six sample points in the sample space.

Types of Events

There are several types of events that occur in Probability. 

Simple Event

An event which includes only one sample point of a sample space is known as a simple event. Here, there is the chance of exactly one outcome. This event is also popularly called Elementary Event. 

Example of a simple event,

Suppose you want heads and so you flip a coin. The probability of getting a heads is only one and can be denoted by E = {Heads}

Similarly, if you toss a die, the probability of getting a 4 is one only. E = {4}

Compound Event

This event opposes the nature of the simple event. Unlike a simple event, it consists of more than one sample point of a sample space, meaning the probability for an outcome to happen is more than one. It can be two or even more events together. 

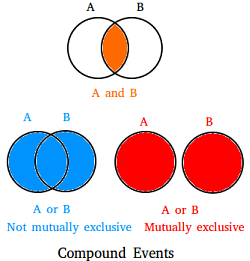
Example of a compound event,

There is a deck of cards and you want to pull out a spade. We know in a standard deck there are a total of 52 cards, so the probability for pulling out a spade becomes 13/52 unquestionably. Again, when we throw a die, the possibility for an even number to appear is more than one (E = {2, 4, 6}) and can be called a compound event.

 Certain or Sure Event

This is a kind of event which is surely going to occur or happen. The probability of these kinds of events is 1. 

Example of a sure event,

Christmas falls in December or Christmas comes once in a year’s holiday. We know for sure that unless the world collapses, Christmas will come with all its cheer. Therefore, the probability of this event is one. 

Impossible Event

 The event which we are sure cannot happen or is impossible to occur is known as an impossible event. The probability of this event is 0. 

 Example of an impossible event,

The sun going around the earth is an impossible event, rolling a 7on a six sided die are called impossible events. Also, suppose you draw a card, the probability of that card drawn to be both red and black is impossible and cannot happen. 

Equally likely Events

Events in which the outcomes are equally possible to happen, are known as equally likely events. 

Example of an equally likely event is, 

Getting an even number on the tossing a die and getting an odd number on the toss of a die are equally likely events, since the probabilities of each event are equal. It means, I can also get a 2, 4, 6 or even a 1, 3 or 5. Like during a coin toss you can either get a head or a tail.

Complementary Events

Two events are said to be complementary when one event occurs only when the other does not occur. Basically complementary events are events that cannot occur at the same time. The probabilities of two complementary events is 1. 

Example of a complementary event,

When a coin is tossed, getting heads and a tail is a complementary event. I can only get a head, when a tail doesn't appear and vice versa. When a die is thrown, getting a 4 or more and rolling a 3 or less are complementary events. 4 or more will only be rolled if it isn't 3 or less. 

Mutually Exclusive Events

Two events can be called mutually exclusive events when both of them cannot occur exactly at the same time. These types of events always have a different outcome. 

If the occurrence of one event prevents the occurrence of another event, such events are mutually exclusive events. It implies that the two events don’t have any common ground to bond. 

Example of a mutually exclusive event is, 

if S = {1 , 2 , 3 , 4 , 5 , 6} and E1, E2 are two events such that E1 consists of numbers less than 3 and E2 consists of numbers greater than 4.

So, E1 = {1,2} and E2 = {5,6} .

Then, E1 and E2 are mutually exclusive. 

NOTE * (COMPLEMENTARY EVENTS CAN BE MUTUALLY EXCLUSIVE, BUT MUTUALLY EXCLUSIVE EVENTS CANNOT BE COMPLEMENTARY)

Independent and Dependent Events

If the occurrence of an event remains uninfluenced by any other event, then we can call it an independent event. However, in probability, where the occurence of one event is affected by another is known as dependent events. 

Example of an independent event is, 

Putting on your favourite nail paint and failing a test, or winning a game of charades and drinking milk. These pairs of activities do not influence each other in any way and therefore are independent of each other. 

Example of a dependent event is,

Getting into an accident because of rash driving, remaining hungry at night because you ended up cooking burnt food, getting yourself fined because you parked your vehicle in the middle of the road, can all be called as dependent events. One event’s outcome leads to another. 

Exhaustive Events

A set of events are called exhaustive, if at least one of them occurs definitely whenever the experiment is performed. It means the probability of any one of them to happen is 100%. In this kind of an event, all events come together to take up the entire sample space.  

Example of an exhaustive event,

Suppose you appear for an exam. The outcomes are you either will pass, or you will fail. When you toss a coin, the total number of possibilities are two. You either get a head, or you get a tail. 

OR event

Two events belong to this OR group, then we consider either of them or both. For example E1 and E2 are two events. If they are associated with this group, then they are considered together( E1 OR E2). The OR group or event is denoted by the union symbol (∪).  

AND Event

Let us consider two events as E1 and E2, and they are associated with AND, it implies the elements which are common to both the events. This event is denoted by the intersection symbol (∩).

E1 ∩ E2 means E1 and E2. 

Things to Remember

• Probability is a branch of mathematics and is solely concerned with the likeability of events happening. An impossible event is denoted by 0, whereas 1 denotes that it is likely to happen. The set of all possible outcomes of an experiment is known as sample space. Each outcome included in a sample space is called a sample point.
• There are different kinds of events in probability which have made arithmetic calculations much easier. These are simple events, compound events, certain or sure events, impossible events, equally likely events, complementary events, mutually exclusive events, exhaustive events. Each one of them has its own individual property and helps in solving problems. 
• The whole theory of probability came into existence in a very typical manner. It goes way back to 1654, when a gambler named Chevalier de Mere approached the French philosopher and popular mathematician Blaise Pascal in concern with some problems related to dice. Blaise further took to discussing these problems with another French mathematician Pierre de Fermat and they finally ended up with the solutions. Later they made it into a theorem. 
• The theory of probability has wider applications in our everyday life. They help in assessing risk management, and are also used as a means to determine the stock market. They help traders make important decisions and are crucial in actuarial science. Even governments apply this theory in environmental regulation and controlling the financial sector. 
• Probability also has a great contribution in science, both medical and biological. They help in determining the weather, act as important tools in statistics, commerce, artificial intelligence, machine learning and game theory. It is the most important aspect of gambling, because, gambling itself means placing a bet upon an event, on its favourability of happening or not. It's also used extensively in philosophy and helps in finding out the frequency and range of different events.