
Content Strategy Manager
Polynomial Formula expresses a polynomial expression and includes variables with different power and the highest power of the variable in the expression is known as the degree of the polynomial. The polynomial formula is also called the standard form of polynomials where the arrangement of the variables is according to the decreasing power of the variable in the given expression. A polynomial is a mathematical and algebraic equation made up of variables and coefficients. One can perform arithmetic operations such as addition, subtraction, multiplication and also non-negative integer exponents for polynomial expressions but not division by variable. Polynomials are universally employed to express numbers as a consequence of operations in mathematics. Polynomial equations are an example of the first few equations you'll learn to solve in Algebra. Because these equations exist in a variety of shapes and rules, it's critical that we fully comprehend what they are and what they represent, as well as how to change them. In simpler terms, a polynomial is an algebraic expression that has more than two algebraic terms or we can say that polynomials are a repetitive addition of a monomial or a binomial.
| Table of Contents |
Key Terms: Polynomials, Equation, Linear, Quadratic Equation, Algebraic Expression, Variables, Terms, Polynomial Formula, Degree, Exponents, Factors, Monomial, Binomial,
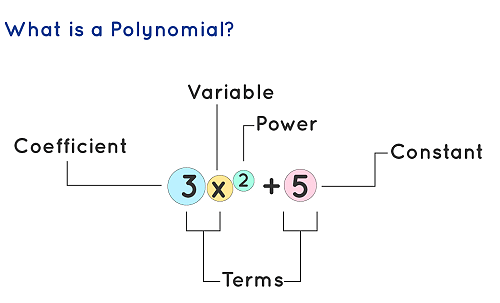
What is a Polynomial?
[Click Here for Sample Questions]
Quadratic functions, for example, are frequently utilised in simulating movements, real-world functions, and a wide range of technology and scientific applications. This is also why we must be able to recognise and solve polynomial equations. To start with, a polynomial is an algebraic expression with non-negative powers for the variables. A polynomial function is an equation with a single independent variable that can appear several times in the equation with varying degrees of an exponent. A polynomial expression can be defined as an algebraic expression with more than two algebraic terms.
Equations with polynomial expressions on both sides are known as polynomial equations. The typical form of a polynomial equation is shown below.
Polynomials may be used to describe the majority of mathematical operations that occur in everyday life. Polynomials may be used to explain summing the costs of things at grocery stores, as well as determining the overall distance traversed by an object or vehicle. In addition, polynomials may be used to calculate the area, perimeter, and volume of various geometrical forms.
Polynomials
The video below explains this:
Polynomials Detailed Video Explanation:
Types of Polynomials
[Click Here for Sample Questions]
There are four forms/types of polynomial equations:
- Monomial: A polynomial with only one term is referred to as a "monomial”.For instance, x2, x, y, 3y, and 4z.
- Binomial: A binomial is a polynomial with two terms such as x2 – 10x
- Trinomial: There are three terms in this sort of polynomial. x2 – 10x + 9 is an example.
- Quadratic: A polynomial with four terms is known as a quadratic polynomial. x3 + 2x2 – 10x + 7 is an example.

Types of Polynomial
For these to be called polynomial expressions, the exponents must be whole integers, and an, an-1,... ao can be any complex number.
The polynomial equation is distinguished from polynomial expressions by the presence of an equal sign followed by another polynomial expression.
The polynomial equation is considered to be in standard form when the terms are ordered from the term with the highest power to the term with the lowest power.
Polynomial Formula
[Click Here for Sample Questions]
The polynomial formula includes variables with different power and the highest power of the variable in the expression is known as the degree of the polynomial. The polynomial formula is also called the standard form of the polynomial where the arrangement of the variables is according to the decreasing power of the variable in the given expression.

Polynomial Formula
If n is a natural number: an – bn = (a – b)(an-1 + an – 2b + … + bn – 2a + bn-1)
If n is even (n = 2k): an + bn = (a + b)(an-1 – an – 2b +…+ bn – 2a – bn-1)
If n is odd (n = 2k + 1), an + bn = (a + b)(an-1 – an – 2b +…- bn – 2a + n-1)
(a + b + c + …)2 = a2 + b2 + c2 + … + 2(ab + ac + bc + ….)
Read More: Introduction, Different Branches of Algebra, Equations
Degree of a Polynomial
[Click Here for Sample Questions]
The highest degree of a monomial within a polynomial is termed the degree of the polynomial.
| Polynomial Equation | Degree | Example |
|---|---|---|
| Linear Equations | 1 | - 3x + 1 = 4x + 5 |
| Quadratic Equations | 2 | x2 – 6x + 9 = 0 |
| Cubic Equations | 3 | x3 – 2x2 + 3x = -5 |
| Quartic Equations | 4 | x4 – 2x2 = -4 |
-
Polynomial Identities
The important polynomial identities are mentioned below:
- (x + y)2 = x2 + 2xy + y2
- (x – y)2 = x2 – 2xy + y2
- x2– y2 = (x + y)(x – y)
- (x + a)(x + b) = x2 + (a + b)x + ab
- (x + y + z)2 = x2 + y2 + c2 + 2xy + 2yz + 2zx
- (x + y)3 = x3 + y3 + 3xy (x + y)
- (x – y)3 = x3 – y3 – 3xy (x – y)
- x3 + y3 = (x + y)(x2 – xy + y2)
- x3 – y3 = (x – y)(x2 + xy + y2)
- x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
Check More:- Polynomials Important Questions
Solving Polynomial Equations
[Click Here for Sample Questions]
Thinking about polynomial equations as the outcome of merging multiple blocks is a fantastic approach to visualise them. We must discover a means to disassemble each block in order to identify the roots, solutions, or solve the polynomial problem.
When solving polynomial equations, keep the following points in mind:
- Rewrite the equation in standard form, with all polynomial expressions on the left side and 0 on the right, if the polynomial equation is still not in standard form.
- Predict the number of zeroes or roots the polynomial equation may have by simplifying it in standard form.
- Apply existing knowledge to solve linear or quadratic equations if the polynomial equation is a linear or quadratic equation.
- Start by looking for one rational element or zero if the polynomial equation has three or more degrees.
- Remove this component and continue the process until you have a linear equation or a constant on your hands.
- Make a list of all the roots and zeros.
-
Equations with Linear Functions
Polynomial equations with a degree of one are known as linear equations. ax + b = 0
We must isolate the unknown variable on one side of the equation while looking for solutions to this sort of equation. Here's where you can hone your skills in solving linear equations.
-
Equations with Quadratic Functions
Quadratic equations are two-degree polynomial equations.
0 = ax2 + bx + c
We can solve quadratic equations in a variety of methods, depending on the shape of the quadratic expression on the right-hand side.
- We may use the zero-property to factor quadratic equations.
- Using particular algebraic features like the difference of two squares, perfect square trinomial qualities, and square completion.
- Finally, the quadratic formula may be used to identify the zeros of quadratic equations.
Polynomial Equations are a kind of polynomial equation (with a degree of 3 or higher). By grouping by factoring, several quartic and cubic equations can be reduced to equations of a lower degree. Finding the real reasons, on the other hand, might be difficult at times.
Also Read:
| Related Articles | ||
|---|---|---|
| Cubic Polynomials | Roots of Polynomials | |
| Remainder Theorem | Zeroes of Polynomial | |
Important Polynomial Theorems
[Click Here for Sample Questions]
Discussed below are some crucial polynomial equation characteristics that we'll need to know in order to determine the real zeros and roots of a polynomial equation quickly.
-
A Function with Real Zeros
The degree of a polynomial function is equal to the number of real zeros it may have. What exactly does this imply? If f(x) has a degree of 5, the number of real zeroes it may have is limited to five.
-
The Signs Rule of Descartes
When we need to identify the zeroes of a polynomial equation without its graph, this rule comes in handy. It reveals the number and location of the zeroes in a polynomial equation.
To use this approach, we'll need to pay attention to the signs of both f(x) and f(y) coefficients (-x). Let's suppose f(x) = 2x4 – 2x3 – 14x2 + 2x + 12 is the case.
The table below describes what the outcome means: Count the number of times the coefficients swap signs.
| Number of zeros from f(x) | With the number sign changes found in f(x), where k is an integer, the number of positive real zeros will be the same (or fewer than by an even integer). |
| Number of zeros from f(-x) | With the number sign changes discovered in f, the number of negative real zeros will be the same (or less than by an even integer) (-x). |
-
Theorem of Rational Zeros
This theorem will assist us in limiting the number of rational zeros that a polynomial function can have. Let p contain all of an's (leading term) factors, and q contains all of ao's factors (constant term).
The polynomial equation's rational zeros may be found by dividing p by q, p/q. Ascertain that the list contains all feasible p/q equations in their simplest form.
We have p = 2 and q = 12 in the same example, f(x) = 2x4 – 2x3 – 14x2 + 2x + 12. Let's go ahead and make a list of all the rational zeros of f. (x).
| Factors of p | ±1, ±2 |
| Factors of q | ±1, ±2, ±3, ±4, ±6, ±12 |
| Possible zeros (p/q) | ±1/12, ±1/6, ±1/4, ± 1/3, ±1/2, ±2/3, ±1, ±2 |
Is this to say that f(x) has 14 rational zeros? No, this TABLE tells us that f(x) will come from this list if it has rational zeros. To put it another way, we've narrowed down the choices from a wide range of rational numbers to a manageable quantity.
Things to Remember
- Polynomial Formula is termed as the standard form of the polynomial where the arrangement of the variables is according to the decreasing power of the variable in the given expression.
- A polynomial is a mathematical and algebraic equation made up of variables and coefficients. A polynomial function is an equation with a single independent variable that can appear several times in the equation with varying degrees of an exponent.
- A polynomial expression is termed as an algebraic expression with more than two algebraic terms. It refers to the repeated addition of a monomial or binomial.
- The primary distinction between polynomials and equations is that an equation is a mathematical statement stating the equivalence of two expressions, whereas a polynomial is a mathematical expression containing variables and constants
Sample Questions
Ques. What are the factors of the given polynomial formula x2 – 10x + 25? (3 Marks)
Ans. x2 – 10x + 25
= x2 – 2(5x) + 52
= x2 – 2(5)(x) + 52
= (x – 5)2
As a result, the factors are (x – 5) and (x – 5) respectively.
Ques. What is the difference between polynomials and equations? (1 Mark)
Ans. The primary distinction between polynomials and equations is that an equation is a mathematical statement stating the equivalence of two expressions, whereas a polynomial is a mathematical expression containing variables and constants.
Ques. Is this statement true or false? The equation g(x) = 0 will always have three real zeros since the polynomial function g(x) has a degree of three. (5 Marks)
Ans. There are only three possible real zeros in the equation g(x) = 0. This means it could have three genuine zeros or none at all. When g(x) = x3 + x, one function can be used to show that the statement is false.
Let's solve the equation for x and see what happens. We'll factor x out and equate x2 + 1 to 0 because the expression is still factorable.
x3 + x = 0
x(x2 + 1) = 0
x = 0
x2 + 1 = 0
x2 = -1
Only when x = -i or x = I will this be true. Despite having a degree of three, this plainly proves that g(x) can't have three genuine zeros. As a result, the statement is false.
Ques. If one of the polynomial's zeroes is 2, get the value of "p" from the polynomial x2 + 3x + p. (3 Marks)
Ans. Because the polynomial’s zero is 2.
We know that if the polynomial p(x) has a zero, then p() = 0.
x = 2 is substituted for x2 + 3x + p
⇒ 22 + 3(2) + p = 0
⇒ 4 + 6 + p = 0
⇒ 10 + p = 0
⇒ p = -10
Ques. Verify the division algorithm by dividing the polynomial f(x)=3x2-x3-3x+5 by the polynomial g(x)=x-1-x2. (5 Marks)
Ans. Given, f(x)=3x2 – x3 - 3x + 5 g(x)=x - 1 - x2
Dividing f(x)=3x2 - x3 – 3x+5 by g(x) = x - 1 - x2
Here,
Quotient = q(x) = x – 2
Remainder = r(x) = 3
By using a polynomial division algorithm,
(Quotient *Divisor) + Remainder = Dividend
So,
[q(x) × g(x)] + r(x) = (x – 2)(x – 1 – x2) + 3
= x2 – x – x3 – 2x + 2 + 2x2 + 3
= 3x2 – x3 – 3x + 5
= f(x)
As a result, the division algorithm has been verified.
Ques. Solve the equation: x2 +16x + 64 = 0 (3 Marks)
Ans. Factors of x2 +16x + 64
The 64 factors are 2, 4, 8, 16, 32, and 64. The total for the middle term is eight.
Now, x2 + (8 + 8) x + 8 * 8
=x2 +8x +8x + 8 * 8
= x(x + 8) + 8 (x + 8)
= (x + 8) (x + 8)
Ques. Solve x3 – 7x2 + 12x = 0 (3 Marks)
Ans. To factor x3−7x2+12x
= x(x2−5x+6)
Now, we factorise x2 − 7x + 12
factors of the 12 = 3, 4
Now, x2 − (3 + 4) x + 3 * 4
=x2 – 3x – 4x + 3 * 4
= x(x – 3) – 4 (x – 3) = (x−3) (x−4)
Factors of x3−7x2+12x are : x (x−3) (x−4)
Ques. Find a quadratic polynomial whose zeros are reciprocals of the zeros of f(x) = ax2 + bx + c, a ≠ 0, c ≠ 0. (5 Marks)
Ans. Let the polynomial f(x) = ax2 + bx + c's zeroes be α and β.
So, α + β = -b/a
αβ = c/a
The zeroes of the needed quadratic polynomial, according to the provided, are 1/α and 1/β.
Now, the sum of zeroes = (1/α) + (1/β)
= (α + β)/αβ
= (-b/a)/ (c/a)
= -b/c
Product of two zeroes = (1/α) (1/β)
= 1/αβ
= 1/(c/a)
= a/c
k[x2 – (sum of zeroes)x + (product of zeroes)] is the needed quadratic polynomial.
= k[x2 – (-b/c)x + (a/c)]
= k[x2 + (b/c) + (a/c)]
Ques. Is there a real zero in the polynomial a4 + 4a2 + 5? (3 Marks)
Ans. Let a2 = x in the aforementioned polynomial.
The polynomial now has the form,
x2 + 4x + 5
When compared to ax2 + bx + c,
Here, b2 – 4ac = 42 – 4(1)(5) = 16 – 20 = -4
So, D = b2 – 4ac < 0
The above polynomial has no actual roots or zeroes because the discriminant (D) is negative.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Check:





Comments