Content Writer
The area of a circle is defined as pi times the radius squared (A=\(\pi r^2\) ), where r is the radius of the circle. It is the space occupied by a circle in a two-dimensional plane. The area inside the boundary of a circle is also determined by the total number of square units inside that circle.
- Area of a circle is determined with the help of Archimedes's formula for the regular polygon.
- It is calculated by the size of the radius of the circle.
- The area of a circle is expressed in terms of square units.
- The circle does not have a volume.
- With the help of the formula, an area of the plot can be calculated.
- It also helps in determining the amount of fencing required for a plot.
- Some real life examples include circular flower beds and dinning plates.
Read More: Areas Related to Circles
| Table of Content |
Key Terms: Area of a Circle, Circumference, Radius, Diameter, Volume, Polygon, Semicircle, Distance, Chord, Secant, Tangent
What is Area of Circle?
[Click Here for Sample Questions]
Area of a circle can be calculated from the diameter and the circumference of a circle. The radius of the circle can be determined from the diameter and the circumference, which will then help in calculating the area of a circle.
- Circumference or Perimeter of a circle is 2πr units.
- It provides precise calculations for crucial parameters.
- The process determines the region occupied by a circle within its boundaries.
- The flower bed in a garden is designed using the concept of the area of a circle.
Area of a circle can be calculated by using the formulas:
Area of a circle, A = \(\pi r^2\) square units
Area = \(\frac{\pi}{4} \times d^2\), where 'd' is the diameter
Area = \(\frac{C^2}{4\pi}\), where 'C' is the circumference
Area = \(\pi \times r^2\), where 'r' is the radius
Solved Examples of Area of a CircleGiven below are the example of a area of circle are as follows: Example 1: If the length of the radius of a circle is 7 units. Calculate its area. Solution: Radius(r) = 7 units(given) Using the formula for the circle's area, Area of a Circle = πr2 Put the values, A = π(7)2 A =π × 49 A = 49π ≈ 154 Answer: The area of the circle is 154 squared units. Read More: Area of Rectangle Example 2: The length of the largest chord of a circle is 14 units. Find the area of the circle. Solution: Diameter(d) = 14 units(given) Using the formula for the circle's area, Area of a Circle = (π/4)×d2 Put the values, A = (π/4) × 142 A = (π/4) × 196 A = 154 |
Read More: Three Dimensional Geometry
What is a Circle?
[Click Here for Sample Questions]
A circle is a closed geometric shape made out of a collection of points that are placed at a fixed distance from the centre of the circle. It is also defined as the locus of two points which are equidistant with respect to each other.
- In the circle, two foci are coincident with each other.
- It is a type of eclipse eccentricity that is calculated to be zero.
- It is divided into two regions, namely the interior region and the exterior region.
- The line passing through the circle forms the line of reflection.
- The formula for a circle in the plane is as follows:
(x-h)2 + (y-k)2 = r2
- where (x,y) are the coordinate points of circle
- (h,k) is the coordinate of the centre of a circle
- r is the radius of a circle.
What is a Circle?
Read More: Perimeter of a Circle
Important Terminologies related to Circle
[Click Here for Sample Questions]
Some important terminologies related to a circle are:
| Term | Description |
|---|---|
| Centre | A point situated in the middle of the circle is called the center of a circle |
| Diameter | A straight line segment that passes through the center of the circle and touches the outer surface of the circle is called the diameter of a circle. It is the longest chord in any circle and is denoted by D or d |
| Radius | A line segment that touches the center and any point of the circle is called the radius of a circle. In other words, the radius is just half of the diameter of a circle. It is denoted by R or r |
| Chord | A line segment inside the circle that touches any two points of a circle is called a chord |
| Secant | A line that passes through any two points on the circle is called the secant of a circle. |
| Tangent | A line that passes through any single point on the circle is called the tangent of a circle |
| Arc | An arc is a fraction of the whole circumference of any circle. It is the part of the curve of a circle |
| Sector | A sector is a part of a circle enclosed by two radii of a circle. We can understand the sector of a circle easily by taking an example of a pizza. The slice of pizza is just a sector of a circle |
| Segment | A region bounded by the chord to the curve of a circle is termed a segment. Any part of a pizza is a segment of a circle |
Read More: Circumference of a Circle
How Do You Find The Area of a Circle?
[Click Here for Sample Questions]
The area of a circle is defined as space or the region it occupies in a two-dimensional plane. It is denoted by A and measured in the square unit, such as m2, cm2, etc.
Formula: The area of the circle can be determined by the given formula
A = \(\pi r^2\)
where r = radius of a circle
d = diameter of a circle
\(\pi\)= constant term C/2r = 22/7 or 3.14
Read More: Trapezoids
Calculation of Area of a Circle
The constant used in the area of a circle calculation is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14. Here’s a table that shows the list of formulae if radius, diameter, or circumference of a circle are given:
| Given Values | Formula |
|---|---|
| Area of a circle when radius is given | A=\(\pi r^2\) |
| Area of a circle when diameter is given | A=\(\frac{\pi d^2}{4}\) |
| Area of a circle when circumference is given | A=\(\frac{C^2}{4\pi}\) |
Read More: Quadrilateral Angle Sum Property
Derivation of Area of Circle
[Click Here for Sample Questions]
To understand the derivation of Area of Circle, look at the image shown below:
Area of Circle Derivation
When a circle is split up into smaller sections and arranged systematically, it forms a shape of a parallelogram. Upon dividing a circle into smaller even sectors, it gradually forms the shape of a rectangle.
The area of a rectangle is = length × breadth
The breadth of a rectangle = radius of a circle (r)
Compare the length of a rectangle and the circumference of a circle, length becomes = \(\frac{1}{2}\) the circumference of a circle
Therefore, Area of circle = Area of rectangle formed = \(\frac{1}{2}(2\pi r) \times r\)
Therefore, Area of the circle is \(\pi r^2\), where r, is the radius of the circle and the value of \(\pi\) is 22/7 or 3.14.
Read More: Remainder Theorem
Area of a Circle Using Diameter
[Click Here for Sample Questions]
Area of circle formula in terms of the diameter is:
Area of a Circle = \(\frac{1}{4} \pi d^2\)
Here 'd' is the diameter of the circle. The diameter of the circle is twice the radius of the circle: d = 2r. From the diameter, calculate the radius of the circle and then find the area of the circle.
Solved Example of Area of a Circle using DiameterGiven below are the example of a area of circle using diameter are as follows: Example 1: The length of the largest chord of a circle is 7 units. Find the area of the circle. Solution: Diameter(d) = 7 units(given) Using the formula for the circle's area, Area of a Circle = (π/4)×d2 Put the values, A = (π/4) × 72 A = (π/4) × 49 A = 38.5 |
Area of Circle Using Diameter
Read More: Area of a Trapezoid Formula
Area of Circle Using Circumference
[Click Here for Sample Questions]
The perimeter or circumference of a circle is measured as the length of outer periphery (complete arc length) of a circle. It is denoted by P or C and measured in millimeters(mm), centimeters(cm), or meters (m).
Area of Circle Using Circumference Formula: \(\frac{(circumference)^2}{4\pi}\)
The perimeter or circumference of a circle is given by a formula C = \(2\pi r\) where, C = circumference or perimeter of a circle
\(\pi\) = 22/7 or 3.14
and, r = radius of a circle
Solved Example of Area of a Circle using CircumferenceGiven below are the example of area of circle using circumference are as follows: Example 1: The circumference of a circle is 44 units. Find the area of the circle. Solution: Circumference of a circle = 44 units Using the formula for the circle's area, Circumference or Perimeter of a circle is 2πr units. 2πr = 44 2 x 22/7 x r = 44 r = 7 Put the values, A = (π/4) × 72 A = (π/4) × 49 A = 38.5 |
Area of Circle Using Circumference: An Example
Read More: Area of Parallelogram
Real-world Example of Area of Circle
[Click Here for Sample Questions]
Prateek and his friends order a pizza and each slice was 12 cm in length.
Let’s calculate the area of the pizza that was ordered by Prateek:
To assume: Length of the pizza slice is equal to the radius of the pizza.
Solution:
A pizza is circular in shape. Thus, area of a circle formula can be used to calculate the area of the pizza.
Radius= 12 cm
Area of Circle formula = \(\pi r^2\) = 3.14 × 12 × 12 = 452.16
\(\therefore\)Area of the Pizza = 452.16 sq. cm
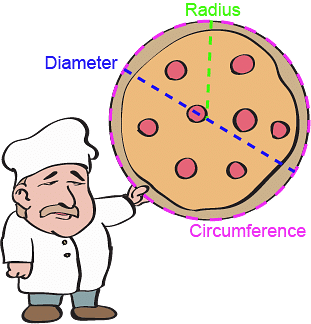
Area of Circle: Real Life Example
Read More: Construction Formula
Things to Remember
- Area of a circle is defined as the total space occupied by a circle in a 2D space.
- A circle can be divided into small sectors, which can be rearranged to form a parallelogram.
- These sectors gradually take the shape of a rectangle.
- One of the sides of the rectangle will be the radius.
- Other sides will be half the length of the circumference.
- The formula for the area of a circle is determined to be πr2 units.
- Circumference of the circle is equal to the length of its boundary.
- Thus, the perimeter of a circle is equal to its circumference, which is 2πr.
- Arc length of the sector of the circle with radius r and angle θ is (θ/360) x 2πr units
- Area of sector of a circle with radius 'r' and θ angle = (θ/360) x πr units.
- Area of segment of a circle = Area of the sector - Area of the triangle.
Read More: Semicircle
Sample Questions
Ques: If the diameter of a circle is 14cm then find the area of the circle? (2 Marks)
Ans: Given d = 14cm
Since r = d/2 = 14/2 = 7cm
then area of circle = πr2
= 3.14×7×7
= 153.86cm
Ques: Find the perimeter of the circle if its radius is 5cm? (2 Marks)
Ans: We know that,
The perimeter of circle = \(2 \pi r\)
= 2×3.14×5
= 31.4cm
Ques: Name the line that touches a single point of the outer periphery of the circle.? (1 Mark)
Ans: The line that travels in any direction and touches any single point on the circumference of a circle is called a tangent.
Ques: Give some examples of circular-shaped objects? (1 Mark)
Ans: The examples of circular-shaped objects are coins, wheels, pizza, rings, round tables, chapatis, etc.
Ques. What are the properties of a circle? (2 Marks)
Ans: Following are the key properties of a circle:
- The circles having equal radii are congruent to each other.
- A set of all points in a circle is always equidistant from the point center.
- Diameter is the longest chord in a circle.
- Diameter of a circle divides the circle into two equal parts called semicircles.
- The circles having a common center and having different radii are known as concentric circles.
Note: A circle does not have a volume because it is a two-dimensional figure.
Ques. Find the area of shaded region in figure, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (3 Marks)
Ans: Area of \(\Delta\)OAB=√3/4(side)2=√3/4 x (12)2
=36√3=36 x 1.73
=62.28 cm2
Area of circle with center O =πr2=3.14 x (6)2
=3.14 x 36 =113.04 cm2
Area of sector(OLQP)=πr2 x θ/360°=3.14 x 62 x 60°/360°
=3.14 x 36 x 1/6 =18.84 cm2
Area of shaded region=area of ΔOAB+area of circle-2 area of sector OLQP
=(62.28+113.04-2 x 18.84)cm2
=137.64cm2
Ques: Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle. (3 Marks)
Ans: Chord of larger circle will be the tangent to smaller circle.
Thus, OC is perpendicular to chord AB and bisects it.
By Pythagoras theorem, in right triangle ACO,
OA2 = OC2 + CA2
a2 = b2 + CA2
\(\sqrt{(a^2-b^2)}\)=CA
AB = 2CA (perpendicular drawn from center bisect the chord)
AB = 2 \(\sqrt{(a^2-b^2)} \)
Ques: TP and TQ are two tangents drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ. (4 Marks)
Ans: Given: Length of taughts drawn from an external point to a circle are equal
\(\therefore\)TP = TQ...(1)
4\(\therefore\) ∠TQP = ∠TPQ (angles of equal sides are equal)...(2)
Now, PT is tangent and OP is radius.
\(\therefore\)OP⊥TP (Tangent at any point pf circle is perpendicular to the radius through point of can’t act)
\(\therefore\) ∠OPT = 90°
or, ∠OPQ+∠TPQ = 90°
or, ∠TPQ = 90° −∠OPQ...(3)
In \(\Delta\)PTQ
∠TPQ + ∠PQT + ∠QTP = 180° (∴ Sum of angles triangle is 180°) or,
90° −∠OPQ + ∠TPQ + ∠QTP = 180°
or, 2(90° −∠OPQ) + ∠QTP = 180° [from (2) and (3)]
or, 180° − 2∠OPQ + ∠PTQ = 180°
Ques: Find the circumference and the area of a circle whose radius is 21 cm. (3 Marks)
Ans: Given: Radius of the circle = 21 cm
Circumference of the Circle = 2πr
= 2 × 22/7 × 21
= 2 × 22 × 2
= 132 cm
Using area of Circle formula = πr2
= 22/7 × 21 × 21
= 22 × 3 × 21
= 1386 sq. cm.
Area of the Circle = 1386 sq. cm.
Ques: The ratio of the area of 2 circles is 16:9. With the help of the area of circle formula find the ratio of their radii. (3 Marks)
Ans: Let us assume the following:
The radius of the 1st circle = R1
Area of the 1st circle = A1
The radius of the 2nd circle = R2
Area of the 2nd circle = A2
It is given that A1:A2 = 16:9
Area of a Circle = πr2
πR12 : πR22 = 16 : 9
Taking square roots of both sides,
R1 : R2 = 4 : 3
Ques: A race track is in the form of a circular ring. The inner radius of the track is 49 yd and the outer radius is 63 yd. Find the area of the race track. (3 Marks)
Ans: Given: R = 63 yd, r = 49 yd.
Let the area of the outer circle be A1 and the area of the inner circle be A2
Area of race track = A1 - A2 = πR2 - πr2 = π(632 - 492) = 22/7 × 1568 = 4,928 square yards.
Ques: The length of the largest chord of a circle is 28 units. Find the area of the circle. (3 Marks)
Ans: Diameter(d) = 28 units(given)
Using the formula for the circle's area,
Area of a Circle = (π/4)×d2
Put the values,
A = (π/4) × 282
A = 616
Ques: Find the circumference and the area of a circle whose radius is 35 cm. (3 Marks)
Ans: Given: Radius of the circle = 35 cm
Circumference of the Circle = 2πr
= 2 × 22/7 × 35
= 2 × 22 × 5
= 220 cm
Using area of Circle formula = πr2
= 22/7 × 35 × 35
= 22 × 5 × 21
= 2310 sq. cm.
Area of the Circle = 2310 sq. cm.
Ques: The ratio of the area of 2 circles is 36:49. With the help of the area of circle formula find the ratio of their radii. (3 Marks)
Ans: Let us assume the following:
The radius of the 1st circle = R1
Area of the 1st circle = A1
The radius of the 2nd circle = R2
Area of the 2nd circle = A2
It is given that A1:A2 = 36:49
Area of a Circle = πr2
πR12 : πR22 = 36 : 49
Taking square roots of both sides,
R1 : R2 = 6 : 7
Ques: Find the circumference and the area of a circle whose radius is 77 cm. (3 Marks)
Ans: Given: Radius of the circle = 77 cm
Circumference of the Circle = 2πr
= 2 × 22/7 × 77
= 2 × 22 × 11
= 484 cm
Using area of Circle formula = πr2
= 22/7 × 77 × 77
= 22 × 11 × 77
= 18,634 sq. cm.
Ques: Find the circumference and the area of a circle whose radius is 70 cm. (3 Marks)
Ans: Given: Radius of the circle = 70 cm
Circumference of the Circle = 2πr
= 2 × 22/7 × 70
= 2 × 22 × 10
= 440 cm
Using area of Circle formula = πr2
= 22/7 × 70 × 70
= 22 × 10 × 70
= 15400 sq. cm.
Ques: A race track is in the form of a circular ring. The inner radius of the track is 7 yd and the outer radius is 14 yd. Find the area of the race track. (3 Marks)
Ans: Given: R = 14 yd, r = 7 yd.
Let the area of the outer circle be A1 and the area of the inner circle be A2
Area of race track = A1 - A2 = πR2 - πr2 = π(142 - 72) = 22/7 × 147 = 4,62 square yards.
Also check:
Comments