
Collegedunia Team Content Curator
Content Curator
Surface Area of Right Circular cone is calculated as π(r + l) r. Right circular cone is one in which the axis is parallel to the base plane. A cone is a three-dimensional geometric shape with a large flat surface and a curving surface that intersect at the summit. The apex or vertex generated at the base of the cone is known as the apex, while the surface layer is known as the base. Whenever a triangle is rotated, one of its two small sides becomes the axis of rotation, forming a cone.
| Table of Content |
Key Terms: Surface Area, Right Circular Cone, Cone Formula, Right Circular Cone Characteristics, Curves Surface Area, Total Surface Area
Also read: Three dimensional geometry
Right Circular Cone
[Click Here for Sample Questions]
A right circular cone has an axis that is parallel to the base plane. A rotating right triangle from one of its legs produces a right circular cone. Right circular cone's base is shaped like a circle. Apex or vertex generated at the base of the cone is known as the apex, while the bottom part is known as the base. When a triangle is turned, one of its two shorter sides becomes the axis of rotation, forming a cone.
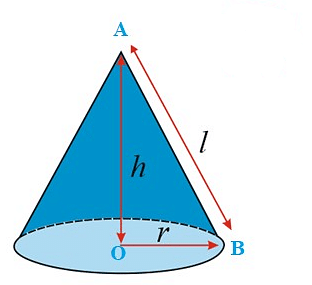
Right Circular Cone
Surface Area of Right Circular Cone
[Click Here for Sample Questions]
The total area occupied by the base of the 3-D dimensional shape is determined as the surface area of a right circular cone. It is measured in square units such as cm2, m2, in2, ft2, and so on. To comprehend the surface area, let's split and open a right circular cone.
We get a segment with a radius equivalent to slant height if we cut a right circular cone (l). The right circular cone's surface area can be divided into two categories:
Curved Surface Area
The region represented by the curved base of a right circular cone is known as the curved surface region. When we talk about the curved surface area of a right circular cone, we don't consider the area of the base. The lateral surface area is another name for the curved surface area.
Total Surface Area
The whole surface area is the space or area represented by a whole area of the right circular cone. T.S.A. is an abbreviated form of T.S.A. The sum of the sections of the curved surface of the cone and the region of the base equals the total surface area of the right circular cone.
A right circular cone's total mass is stated as the surface of a right circular cone. To compute the surface area of a dilemma, we must first determine the entire surface section of the right circular cone.
Also read: Surface Area of Cone
Formula of Right Circular Cone
[Click Here for Sample Questions]
A right circular cone might have two surface areas: curved surface area or total surface area, as we mentioned in the previous section. Different formulas can be used to determine TSA and CSA for a right circular cone.
Formula for Curved Surface Area
The formula for a right circular cone (CSA):
The area of a cone's curved surface = area of a segment with a radius equal to the slant height, namely,'s'.
Curved Surface area=
where,
- h = Height
- r = Base radius
- s = slant height
Total Surface Area Formula
The total surface region of a cone = Area of circular base + Curved surface of a cone (sector's region) is the formula for calculating the TSA of a right circular cone.
Total Surface Area=
- h = Height
- r = Base radius
- s = Slant height
Also read: Surface Areas and Volumes Revision Notes
Parts of Right Circular Cone
[Click Here for Sample Questions]
A right circular cone is referred to by a few words. The cone is divided into three terms. Radius, height, and slant height are the three options. Take a look at the right circular cone presented below:
- Vertex: It is the contact point for all of the cone's curved surfaces. The vertex of the cone is the fixed spot of the cone where the curving lines are united. It's also referred to as the cone's apex.
- Radius: The radius of the foundation of the right circular cone is the distance between any point on the perimeter of the base (circle) and the centre of the base.
- Height: The height of the cone is the gap between the apex or vertex and the centre of the base.
- Slant Height: Slant height is the gap between the vertex and any spot on the circumference of the cone's base.
Characteristics of Right Circular Cone
[Click Here for Sample Questions]
The following are the properties of Right Circular cone:
- It features a circular base with a vertex that connects to the axis of the appropriate cone.
- The length of the side of the cone measured from the vertex to the outermost border of the circular base is the slant elevation of this cone. The letter 'l' stands for it.
- The parallel line from the vertex to the centre position is the altitude of a right cone. It is symbolized by the letter 'h' and correlates with the cone's axis.
- The solid produced here is the needed cone if a right triangle is revolved about its parallel, with the perpendicular as the axis of rotation. The lateral surface area is part formed by the triangle's hypotenuse.
- On the axis of the cone, any segment of a right circular cone perpendicular to the base creates a circle.
- An isosceles triangle is a segment of a right circular cone that comprises the vertex and 2 points of the base.
Things to Remember
- The right circular conical and the oblique cone are two sorts of cones based on the placement of the apex in relation to the base.
- The axis of a right circular cone or regular cone is parallel to its base, whereas the axis of an oblique cone seems inclined and is not perpendicular to the base.
- A right circular cone with a circle base with radius 'r' and height 'h' has a volume equal to one-third of the sum of the base's area and height.
- The entire space covered by the object in a three-dimensional plane is determined by the volume of the right circular cone.
- The vertex is the place where all of the cone's curving surfaces meet. The vertex of the conical is the stable location of the cone where the curving lines are united. This is also termed as the cone's apex.
- Slant height is the gap between the vertex and any spot on the circumference of the cone's base.
Also Read:
Sample Questions
Ques. Explain the Volume of Right Circular Cone? (2 Marks)
Ans. The entire space covered by the object in a three-dimensional plane is determined by the volume of the right circular cone. A cone's volume is measured in cubic units, such as in3, m3, cm3, and so on. A right circular cone with a circular base with radius 'r' and height 'h' has a volume equal to one-third of the sum of the base's area and height. Applying the general formula, we can compute the volume of a right circular cylinder with its base radius and height.
Ques. What is Right Circular Cone Equation? (2 Marks)
Ans. The following is the equation for a right circular cone where vertex is at the source:
Where,
θ− Semi vertical angle
(l,m,n) Axis direction cosines of the Right Circular Cone.
Ques. What is Frustum of the Cone? (2 Marks)
Ans. When a cone is split into two sections by a plane perpendicular to the bottom of the cone, the frustum is the portion of the cone without even a vertex. In cones and pyramids, a frustum is specified. A truncated shape is sometimes known as a frustum. A truncated cone is another term for the frustum of a cone. The frustum of a cone has surface region and volume, much like any 3D object.
Ques. Over the holiday, Ambuj went camping. He finds a tent with a right circular cone form at the campsite and estimates that the elevation of the tent is 3 times the radius (r). Calculate the tent's estimated volume in respect of its radius. (3 Marks)
Ans. The height is 3 times the radius.
h = 3r
The right circular cone Volume can be Derived as follows:
- Cone Volume (V) = (1/3)πr2h
- V = (1/3)πr2(3r)
- V = (1/3) × 3 × πr3
- V = πr3
The volume of the tent is πr3 cubic units.
Ques. Yuktaa is having fun near the river's edge. She sculpted a sand cone with a 5cm radius and a 12cm height. Calculate how much sand was utilised in the cone. (3 Marks)
Ans. The Cone Radius (r)=5cm.
Cone Height (h)=12cm
We are aware that the right circular cone Volume is 13πr2h
V=13×3.14×52×12
V=314cm3
Therefore, the quantity of sand inside the cone is 314cm3.
Ques. Ambika and Yuktaa attended a circus performance. A clown gave them a conical cap on their way home. If the cap's height is 6 inches, the radius is 4 inches, and the slant height is 8 inches, calculate the volume and curved surface area. (5 Marks)
Ans. The dimensions are:
- Radius = 4 inch
- Height = 6 inch
- Slant height = 8 inch
Substitution the values in the cone formula Volume,
- Cone Volume= (1/3) π × r2 × h
- Cubic units = (1/3) π × (4)2 × 6 = 32π in3
- Substitution of the values in the formula,
- Curved surface area of a cone = πrl sq. units = π × 4 × 8 = 32π in2
Therefore, The Cone Volume is 32π in3.
The surface area is 32π in2.
Ques. If the radius is 6 cm and the slant height is 10 cm, calculate the surface area of the right cone. (5 Marks)
Ans. Here,
- Radius (r) is 6 cm
- Slant height (l) is 10 cm
- Cone Surface Area = π r(r + l)
Calculating surface area,
= 3.14 × 6(6 + 10)
= 3.14 × 6 × 16
= 301.44
Hence, Surface area of the right cone is 301.4 sq. cm.
Ques. What is the Difference between Right Circular cone & Oblique Circular cone? (2 Marks)
Ans. The right circular cone and the oblique cone are two sorts of cones determined on the placement of the apex in relation to the base. The right circular cone axis or regular cone is parallel to bottom and the axis of an oblique cone has a slight bend and is not perpendicular to the foundation. There are no equations for the sections of oblique cones since the slant height is indeterminate.
Also read:






Comments