
Content Curator
Surface area of a triangular prism is the sum of the areas of all the faces of the prism. It is determined with the formula:
Surface area = bh + L (s1 + s2 + s3)
where,
b is the bottom edge of the base triangle,
h is the height of the base triangle,
s1, s2, and s3 are the sides of the triangular bases
L is the length of the prism and
(bh) is the combined area of the two triangular faces [2 × (1/2 × bh)]
| Table of Content |
Key Takeaways: Triangular Prism, Right Triangular Prism, Lateral Surface Area, Uniform Triangular Prism
What is a Triangular Prism?
[Click Here for Sample Questions]
Triangular prism is a polyhedron with two triangular bases and three faces joining corresponding sides of the triangular bases. By extending the face of a base triangle in either direction normal to its face, a triangular prism is formed. It's similar to stacking numerous very thin triangles face to face. Thus, all cross-sections parallel to the triangular base are the same. It has six vertices, five faces and nine edges.
A right triangular prism has two triangle faces that are parallel and congruent, as well as three rectangular faces that join the triangular faces. It has five sides, including two right triangles and three rectangles.
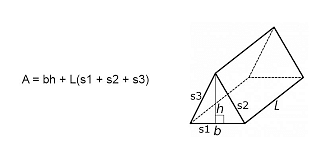
Surface Area of a Triangular Prism
Also Read:
| Related Articles | ||
|---|---|---|
| Surface Area of Rectangular Prism | Types of Triangles | Triangle Theorems |
| Perimeter of Parallelogram | Laws of Vector Addition | Vector Formula |
| Parallelogram | Types of Polygon | Quadrilaterals |
Derivation of Surface Area of Triangular Prism
[Click Here for Sample Questions]
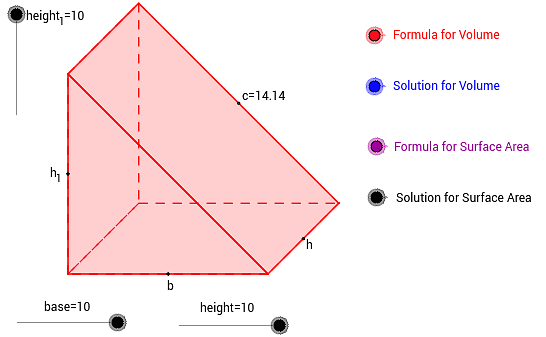
The surface area of a triangular prism is obtained by adding all the surface areas of faces that constitute the prism. Consider the prism below:
A Triangular Prism
The sum of areas of the parallelograms joining the triangular base is equal to the product of the perimeter of the base and length of the prism. The area of the two triangular bases is equal to;
[2 × (1/2 × bh)] = bh
Thus, the formula for the surface area of a triangular prism is:
Surface area = (Perimeter of the base × Length of the prism) + (2 × Base Area)
Surface area = (S1 +S2 + S3) L + bh
where;
b is the resting side of the base triangle,
h is the height of the base triangle,
L is the length of the prism and
S1, S2, and S3 are the three sides of the base triangle
Lateral Surface Area of Triangular Prism
[Click Here for Sample Questions]
Lateral Surface area is the surface area of the prism without the triangular base areas. It is the sum of all the areas of the vertical faces.
Thus, the lateral surface area of a triangular prism is:
Lateral Surface Area = (S1 + S2 + S3) × L
= (Perimeter × Length) or LSA = p × l
where;
l is the height (length) of a prism
p is the perimeter of the base
Surface Area of Right Triangular Prism
[Click Here for Sample Questions]
A right triangular prism has two parallel and congruent triangular faces and three rectangular faces that are perpendicular to the triangular faces.
Area of the two base triangles = 2 × (1/2 × base of the triangle × height of the triangle) which simplifies to 'base × height' (bh).
Lateral surface area is the product of the length of the prism and the perimeter of the base triangle = (S1 + S2 + h) × l.
Thus, adding all the areas, the total surface area of a right triangular prism is given by,
= (S1 + S2 + h) × l + bh
where;
b is the resting side of the base triangle,
h is the height of the base triangle,
L is the length of the prism and
S1 and S2 are the three sides of the base triangle
Right Triangular Prism
Also Read: Angle Sum Property of Quadrilateral
Surface Area of Uniform Triangular Prism
[Click Here for Sample Questions]
A right triangular prism with equilateral bases and square sides is called a uniform triangular prism.
Since it is an equilateral triangle S1 = S2 = S3 = b
Therefore,
Surface area of Uniform Triangular Prism = 3 bL + bh
where;
b is the bottom edge of the base triangle,
h is the height of the base triangle,
L is the length of the prism and
(bh) is the combined area of the two triangular faces [2 × (1/2 × bh)]
Also Read:
Things to Remember
- Surface area of a triangular prism is equal to (S1 +S2 + S3)L + bh
- Lateral surface area of a triangular prism is equal to (S1 +S2 + S3)L
- Surface area of a right triangular prism is equal to (S1 + S2 + h) × l + bh
- Surface area of a uniform triangular prism is equal to 3bL+bh
Sample Questions
Ques. Calculate the surface area of a triangular prism with side 7 cm, base 5 cm, and height 6 cm. (3 marks)
Ans. The formula for the surface area of a triangular prism is
= bh +3bL
Given,
h = 7, b = 5, L = 6
Using the formula;
= (7×5) + 3 (5×6)
= 35 + 90 =125
So, the surface area of the given triangular prism is 125 cm².
Ques. The bases of a triangular prism are formed by a right triangle with leg lengths of 4cm and 7cm. The lateral faces of the prism are formed by a rectangle with a length of 5cm. Find the surface area of the triangular prism. (3 marks)
Ans. Given; b = 4, h = 7, s1 = 4, s2 = 7, L = 5
S3 is the hypotenuse of the right triangle and can be found using the Pythagoras theorem
(s3)² = 16 + 49
s3 = 8.062
A = (S1 + S2 + h) × l + bh
A = (4 + 7 + 8.062) (5) +(4)(7) .
A = 123.31
The surface area of the right-angled triangular prism is 123.31 cm².
Ques. If we are given a triangular prism that has a base formed by an equilateral triangle of 6 cm, and length 10 cm, find the surface area? (3 marks)
Ans. Since it is an equilateral triangle s1 + s2 + s3 = 3s1.
Also, we can set b = s1. So, 3s1 = 3b.
A = bh + 3bL.
A = (6×6) + 3(6×10)
A = 36 + 180
A = 216 cm2
Ques. Find the total surface area of a right triangular prism which has a base area of 60 square units, the base perimeter of 40 units, and the length of the prism is 7 units. (3 marks)
Ans. Given, base area = 60 square units
base perimeter = 40 units
length of prism = 7 units
Thus, the surface area of the right triangular prism,
Surface Area = (Perimeter of the base × Length of the prism ) + (2 × Base Area)
A = (40 × 7) + (2 × 60)
A = (280 + 120)
A = 400 square units
Ques. If the height of the prism is 4cm and the length of the side of the equilateral triangular base is 6cm. Then find the area of the prism for the above example. (3 marks)
Ans. Base = 5cm, h = 10cm, b = 15cm, L = 4cm
s1 = s2 = s3 = 6cm.
By the formula,
Area of the Triangular Prism = [bh + ( s1 +s2 + s3) L]
Area = [5 × 10 + (6 + 6 + 6) 4]
= [50 + (18) 4] = 50 + 72
= 122 cm²
Ques. The cross section of a uniform prism is a right-angled triangle with sides 3cm, 4cm and 5cm. If its length is 10cm. Calculate the total surface area. (2 marks)
Ans. P = perimeter of bases = 3 + 4 + 5 = 12cm
H = height = 10cm
PH = 12 10 = 120cm2
B = area of the base = 1/2(bh) = 1/2(34) = 6cm2
surface area of prism
= 120 + 2(6)
= 132 cm2
Ques. The Cross section of the uniform triangular prism with side 4cm .If its length is 10cm,calculate the total surface area. (5 marks)
Ans. Given; b = 4cm, L = 10cm
Using Pythagorean theorem,
Height of the base triangle = h² = b² + (b/2)²
= 4² + 2²
= 16 + 4
= 20
h = 4.5cm
Surface area of a uniform triangular prism = 3bL+bh
= 3 (4×10) + (4×4.5)
= 120 + 18
= 138 cm²
Ques. A triangular prism has a triangular end with a base of 5 inches and a height of 4 inches. The length of each side is 8 inches and the width of each side is 6 inches. What is the surface area of the prism? (3 marks)
Ans. Given;
s1 = s2 = 6 inches
s3 = b = 5 inches
L = 8 inches
h = 4 inches
The surface area of a triangular prism is equal to (S1 +S2 + S3)L + bh
= (6+6+5) 8 + (5×4)
= 136 + 20
= 156 in²
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Check:





Comments