
Collegedunia Team Content Curator
Content Curator
Total Surface Area of Hollow Cylinder is calculated by adding all areas on the surface: the areas of the base, top, and lateral surfaces (sides) of an object. The total surface area of a hollow cylinder is given by the formula:
Total Surface Area of Hollow Cylinder (TSA) = \(2\pi (r_1 + r_2)(r_1-r_2+h)\)
A hollow cylinder is hollow on the inside and has a radius difference between the interior and outside radius. Some classic examples of hollow cylinder are tubes, circular towers, or straws. A cylinder can thus be defined as a solid surface created by a line traveling parallel to a fixed line, with its end describing a closed figure in a plane.
The lateral surface area of a hollow cylinder is the area covering the circular surface without the two bases of the cylinder. It is given by the formula:
LSA of a hollow cylinder (LSA) = \( 2\pi r_1 h + 2\pi r_2 h\)
Read Also: Surface Areas and Volumes Revision Notes
| Table of Content |
Key Terms: Hollow Cylinder, Total surface area, Lateral Surface Area, Curved Surface Area, Radius, Height, Thickness, Circumference, TSA, CSA, LSA
What is Hollow Cylinder
[Click Here for Sample Questions]
Hollow Cylinder is a three-dimensional object with two flat surface, one at the top and the other at the bottom. As the cylinder is hollow, these flat surfaces are like concentric circles with inner radius r and outer radius, R. The hight of the cylinder is h. Let us visualise this with a figure as follows:
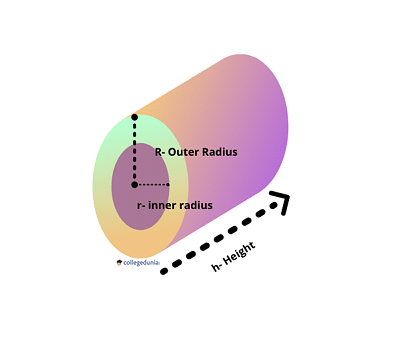
Hollow Cylinder
The radius of the flat surface that is vacant on the inside and has a thickness, is based on the difference between the inner and outer radii. In other words, a hollow cylinder is defined by two parallel cylindrical surfaces and two parallel circular bases that are carved out of two parallel planes by these two cylindrical surfaces.
Also Check:
Total Surface Area of Hollow Cylinder
[Click Here for Sample Questions]
The total surface area of a hollow cylinder is given by the formula:
TSA= 2π ( r1 + r2)( r1 – r2 + h)
Where,
r1 = the outer radius of the given cylinder
r2 = the inner radius of the given cylinder
h= height of the given cylinder
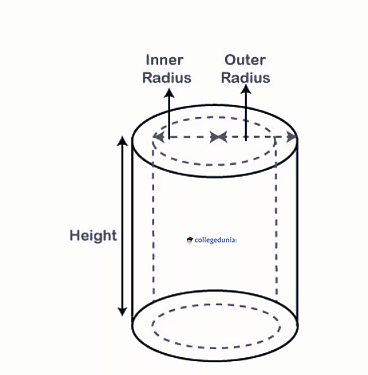
Dimensions of Hollow Cylinder
The total surface area of a hollow cylinder can thus be defined as the sum of the lateral surface area of the cylinder and the area of the two circular hollow bases.
Read More: Circle
Lateral Surface Area of a Hollow Cylinder
[Click Here for Sample Questions]
Lateral surface area of a hollow cylinder is the curved surface area of the cylinder without the bases. If C1 and C2 are the inner and outer circumferences of a hollow cylinder.
The Circumference of a circle (C) is given by:
\(C=2\pi r \), therefore, \(C_1=2\pi r_1\) \(C_2=2\pi r_2\)
Let t = the thickness of the cylinder (r1 – r2)
The Lateral Surface Area, LSA (L), for a cylinder, is:
\(L=C\times h = 2\pi r h\)

LSA of Hollow Cylinder
Therefore,
\(L_1= 2\pi r_1 h\)....……… the external curved surface area
\(L_2= 2\pi r_2 h\) ..……….. the internal curved surface area
Thus,
LSA of a hollow cylinder = L = \(2\pi r_1 h + 2\pi r_2 h\)
Read More: Difference Between cube and Cuboid
Deriving TSA of a Hollow Cylinder
[Click Here for Sample Questions]
We know that,
LSA of a hollow cylinder\(= L= 2\pi r_1 h + 2\pi r_2 h\)
Cross-sectional Area can be calculated as:
Let A be the area of a cross-section of a hollow cylinder,
\(A = \pi r^2\), for a circle, therefore,
\(A_1 = \pi r_1 ^2\) for the area enclosed by \(r_1\)
\(A_2 = \pi r_2 ^2\) for the area enclosed by \(r_2\)
\(A = A_1 - A_2\) for the cross-sectional area of a hollow cylinder
\(A = \pi r_1 ^2 - \pi r_2 ^2 = \pi (r_1 ^2 - r_2 ^2)\)
The different forms of evaluating the TSA of a hollow cylinder based on the given parameters can be summarized as:
- \(2\pi h(r_1+r_2) + 2\pi (r_1^2-r_2^2)\)
- \(2\pi h(r_1+r_2) + 2\pi (r_1+r_2) (r_1-r_2)\)
- \(2\pi (r_1+r_2)(h+r_1-r_2) \)
Read More: Three-Dimensional Geometry
Solved ExamplesExample 1: What is the weight, lateral surface area, and total surface area of a steel pipe whose interior and exterior diameters measure 15cm and 17cm respectively, and length 10m; one cubic cm of iron weighing 0.8gm. Solution: Here, d = 15cm r = 7.5cm D = 17 cm R = 8.5 cm h = 10 m = 1000 cm Volume=π(R2−r2)h = π(72.25–56.25)1000 = 50265.48cm3 Weight = Volume x density = 50265.48 x 0.8 = 40212.39 g Lateral surface area= 2π(R+r) h = 2π(8.5+7.5)1000 = 2π×16×1000 = 100530.96cm2 Since, Total surface area of the pipe = Lateral surface area of pipe + Area of bases = 100530.96+100.53100530.96+100.53 = 100631.49cm2 Example 2: A hollow cylinder copper pipe is 21dm long, and its outer diameter and inner diameters are 10cm and 6cm respectively. Find out the volume of copper used in manufacturing the pipe. Solution: Given, The height of the cylindrical pipe is h = 21dm = 210cm Thus, External radius, R=10/2 =5 cm Internal radius,r = 6/2 = 3cm The volume of the copper used in manufacturing the pipe = Volume of the external cylinder − the volume of an internal cylinder = πR2h−πr2h = π(R2−r2)h = 227[52−32] × 210 = 227 × 16 × 210 = 22 × 16 × 30 = 10560 cm3 |
Parts of a Cylinder
[Click Here for Sample Questions]
A hollow cylinder comprises the following parts:
Sides and Base
A cylinder is a solid that is commonly encountered in everyday life, such as a straw. On deconstructing a hollow cylinder, we see that it has two roundish closures called bases. The bases are all the same and run in the same direction. If you managed to 'unroll' the cylinder, you'd see that when straightened out, the side is really a rectangular form.
Height
The perpendicular distance between the two bases is the height h. When calculating the volume of a tilted cylinder, it is critical to utilize the perpendicular height ('altitude').
Radius
A cylinder's radius r is equal to the radius of the base. Radius can be calculated as half of the diameter.
Axis
A line that connects the two bases' centers forms the axis of the hollow cylinder.
Let us look at the following diagram to visualize the parts of a hollow cylinder.

Parts of Hollow Cylinder
Read More: Surface Areas and Volume
Things to Remember
[Click Here for Sample Questions]
- A hollow cylinder is a three-dimensional object which is empty on the inside and has a thickness.
- A solid cylinder is made up of solid circles with no gap in between whereas a hollow cylinder is made up of circular rings (hollow circles).
- A hollow cylinder's cross-section is the two end portions circumscribed by two concentric circles ( rings formed by circles).
- The total surface area (TSA)of a cylinder is given by: 2π ( r1 + r2)( r1 – r2 + h).
- The lateral surface area (LSA) of a hollow cylinder is given by: 2π r1h+ 2π r2h.
- The cross-sectional area of a hollow cylinder is given by: π(r12-r22).
Area of Hollow Cylinder PDF
Also Read
| Concepts Related to Area of Geometric Figures | ||
|---|---|---|
| Circumference of a Circle | Sphere | Areas Related to Circle |
| Formula of Perimeter Shapes | Diameter Formula | Surface Area of a Cylinder Formula |
Sample Questions
Ques. The length of a copper hollow cylinder pipe is 21dm. Its outside and inner diameters are 10 and 6 cm, respectively. Calculate the amount of copper utilized to make the pipe. (3 Marks)
Ans. Given that:
The height of the cylindrical pipe is h=21 dm=210cm
Thus, the External radius, R=102=5cm
Internal radius, r=62=3cm
The amount of copper utilized in the pipe's construction.
= Volume of external cylinder−volume of an internal cylinder
= \(\Pi R^2 h - \Pi r^2 h\)
= \(\Pi (R^2 - r^2)h\)
= 227[52−32]×210=227×16×210
= 22×16×30
= 10560 cm3
Ques. A round well has a diameter of 2.1 meters and a depth of 21 meters. Calculate the cost of plastering a circular well's inside surface at a rate of Rs. 40 per m2. (3 Marks)
Ans. Given: Radius of the circular well (r) = 2.1 m, depth (h) = 21 m
The inner surface of the well, which is the total of the curved surface area and the base area, must be plastered.
Area to be plastered = Curved surface area + Area of base
= \(2\pi r h + \pi r^2\)
= 2×227×2.1×21+227×(2.1)2
= 277.2+13.86
= 291.06m2
Cost of1m2 of well=Rs.40
Cost of 291.06 m2 of well = Rs. (40 × 291.06) = Rs. 11642.40
Ques. Calculate the curved surface area of a hollow cylinder with a thickness of 2cm, an exterior radius of 8 cm, and a height of 20 cm. (3 Marks)
Ans. Let the hollow cylinder's exterior radius, internal radius, and height be \(r_1\),\(r_2\) and \(h\) respectively.
\(r_2\)=8-2=6 cm
The curved surface area of a hollow cylinder \(= 2 \pi r_1h + 2 \pi r_2h =\)
\(= 2 \pi h(r_1 + r_2)\)=2×227×20(8+6)=1760 cm2
Ques. A solid right circular cylinder's curved surface area and circumference at the base are 4400 cm2 and 110 cm, respectively. Find out how tall it is and how wide it is. (4 Marks)
Ans. CSA of cylinder = 4400 cm2
Circumference of the base = 110 cm
\(2\pi r\) = 110 ==> 2 x (22/7) x r = 110
r = 110 x (1/2) x (7/22)
r = 17.5 cm
diameter = 2r = 2(17.5)
diameter = 35 cm
\(2\pi rh\) = 4400
110 ⋅ h = 4400
h = 4400/110
h = 40 cm
Height = 40 cm
Diameter of the cylinder = 35 cm
So, the height and diameter of the cylinder is 40 cm and 35 cm respectively.
Ques. Find the weight, lateral surface area, and total surface area of a steel pipe with a length of 10m and interior and exterior diameters of 15cm and 17cm, respectively; one cubic cm of iron weighs 0.8g. (4 Marks)
Ans. Here d = 15cm r = 7.5cm
D = 17 cm R = 8.5 cm
h = 10 m = 1000 cm
Volume=\(\Pi (R^2-r^2)h\)
= π(72.25–56.25)1000
= 50265.48cm3
Weight = Volume x density = 50265.48 x 0.8 = 40212.39 g
Lateral surface area=2π(R+r)h
= 2π(8.5+7.5)1000
= 2π×16×1000
= 100530.96cm2
Total surface area of the pipe=Lateral surface area of pipe+Area of bases
= 100530.96+100.53
= 100631.49cm2
Ques. Each of the 12 right cylindrical pillars in a mansion has a radius of 50 cm and a height of 3.5 m. At $ 20 per square metre, calculate the cost of painting the curving surface of pillars. (4 Marks)
Ans. The pillars of the mansion are in the shape of cylinder
Radius = 50 cm ==> 0.5 m
Height = 3.5 m
CSA of one pillar = 2 x (22/7) x 0.5 x 3.5
= 2 x 22 x 0.5 x 0.5 ==> 11 m2
CSA of 12 pillars = 12 x 11
= 132 m2
Cost to paint per m2 = $ 20
Total cost = 20 x 132
= $ 2640
Hence, the total cost of painting 12 pillars is $ 2640
Ques. A solid right circular cylinder has a total surface area of 1540 cm2. Find the cylinder's Curved Surface Area if the height is four times the radius of the base. (5 Marks)
Ans. Total surface area of cylinder = 1540 cm²
CSA of cylinder + top area + bottom area = 1540 cm²
\(2 \Pi r(h+r)\) = 1540
h = 4 x radius of the base
h = 4 r
\(2 \Pi r(4 r+r)\) = 1540
\(2 \Pi r(5r)\) = 1540
2 x (22/7) x 5 r2 = 1540
= 1540 x (1/2) x (7/22) x (1/5)
= (1540 x 7)/(2 x 22 x 5)
= (1540 x 7 )/(2 x 22 x 5)
r2 = 49
r = √(7⋅7)
r = 7 cm
Curved surface area of cylinder :
= 1540 - 2 x (22/7) x 7 x 7
= 1540 - 308
= 1232 cm2
Hence, CSA of cylinder = 1232 cm2.
Ques. What is the formula for the total surface area of a hollow cylinder? (1 Mark)
Ans. A hollow cylinder is made up of two thin sheets of a rectangle having a length and breadth. Also, the radius of both the cylinders can be r1+r2. Thus, the total surface area of the cylinder is equal to the surface area of both the rectangles which is equal to 2π( r1 + r2)( r1 – r2 +h).
Ques. How many faces vertices does a hollow cylinder have? (1 Mark)
Ans. A cylinder has 3 faces - 2 circle ones and a rectangle (if you take the top and bottom off a tin can then cut the cylinder part on the seam and flatten it out you would get a rectangle). It has 2 edges and no vertices (no corners).
Ques. Find the volume of a hollow cylinder having inner radius = 6 cm, outer radius = 8 cm and height = 7 cm. (3 Marks)
Ans. Given:
Inner radius of the hollow cylinder (r) = 6 cm
Outer radius of the hollow cylinder (R) = 8 cm
Height of the hollow cylinder (h) = 7 cm
Volume of the given hollow cylinder = π (R2- r2) h = (22/7)(82 - 62)(7) = 22(64 - 36) = 616 cm3
Volume of the given hollow cylinder = 616 cm3
Ques. The volume of a hollow cylinder is 440 cm3. If the outer radius = 14 cm and inner radius = 12 cm. Find the height of the cylinder. (3 Marks)
Ans. Inner radius of the hollow cylinder (r) = 6 cm
Outer radius of the hollow cylinder (R) = 8 cm
Volume of the hollow cylinder (V) = 440 cm3
Let h be the height of the hollow cylinder.
Volume of the hollow cylinder = 440 = π (R2 - r2) h = (22/7)(142 - 122) h = (22/7) 52 × h
Therefore, h = (440/1144) × 7 = 2.692 cm ≈ 2.7 cm
Ques. What Is the unit used to express Volume of Hollow Cylinder? (2 Marks)
Ans. The volume of the hollow cylinder can be expressed in cubic units, like m3, cm3, ft3, in3, yd3, etc. Other common units used are liters(l) and millimeters(ml).
Ques. How do you find the Volume of a Hollow Cylinder if only base area and height is given? (2 Marks)
Ans. The volume of a cylinder is the total capacity of the cylinder. Therefore, signifying the amount of any material that can be immersed in it or the amount of any material it can hold. From the definition, the volume of the Cylinder = Base Area × Height.
Ques. If one litre of paint covers 10 m2, how many litres of paint is required to paint the internal and external surface areas of a cylindrical tunnel whose thickness is 2 m, internal radius is 6 m and height is 25 m. (4 Marks)
Ans. Given that, height h = 25 m; thickness = 2 m.
internal radius r = 6 m
Now, external radius R = 6 + 2 = 8 m
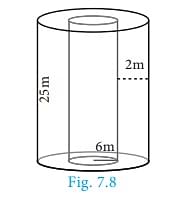
C.S.A. of the cylindrical tunnel = C.S.A. of the hollow cylinder
C.S.A. of the hollow cylinder = 2π(R + r)h sq. units
= 2 × (22/7) (8 + 6)×25
Hence, C.S.A. of the cylindrical tunnel = 2200 m2
Area covered by one litre of paint = 10 m2
The number of litres required to paint the tunnel = 2200/10 = 220.
Therefore, 220 litres of paint are needed to paint the tunnel.
Ques. The total surface area of hollow cylinder, which is open from both sides, is 3575 cm2; area of the base ring is 357.5 cm2 and height is 14 cm. Find the thickness of the cylinder. (5 Marks)
Ans. Let the inner radius be r and outer radius be R
Base Ring =π(R2−r2)=357.5 cm2
(R2−r2)=357.5÷22/7
(R+r)(R−r)=(3575∗7)/220
(R+r)(R−r)=113.75 sq cm............(1)
Total surface area of the cylinder =3575 sq cm
Now, total surface area of a hollow cylinder = outer curved surface + inner curved surface area + 2(Area of the circular base)
=2πRh+2πrh+2π(R2−r2)
=2πRh+2πrh+2∗357.5=3575
=2πh(R+r)+2×357.5=3575
=2πh(R+r)+751=3575
=2πh(R+r)=3575−751
=2×22/7×14×(R+r)=2824
=(R+r)=44∗142824∗7
=(R+r)=32
Substituting the value of (R+r)=32 in equation (1), we get.
(R+r)(R−r)=113.75
32(R−r)=113.75
R−r=113.75/32
Thus, the thickness of the cylinder is 3.55 cm
Ques. The hollow cylinder has a height of 70 cm, an outer diameter of 180 cm, and an inner diameter of 120 cm. What is the surface of the body, including the area inside the cavity? (4 Marks)
Ans. h=70 cm
D1=180 cm
D2=120 cm
o1=π⋅ D1=3.1416⋅ 180≐565.4867 cm
o2=π⋅ D2=3.1416⋅ 120≐376.9911 cm
S1=π⋅ (D1/2)2=3.1416⋅ (180/2)2≐25446.9005 cm2
S2=π⋅ (D2/2)2=3.1416⋅ (120/2)2≐11309.7336 cm2
M=2⋅ (S1−S2)=2⋅ (25446.9005−11309.7336)≐28274.3339 cm2
S=M+o1⋅ h+o2⋅ h=28274.3339+565.4867⋅ 70+376.9911⋅ 70=94247.7796 cm2=9.425⋅104 cm2
Ques. A solid right circular cylinder has radius of 14 cm and height of 8 cm. Find its CSA. (3 Marks)
Ans. Radius of the cylinder (r) = 14 cm
Height of the cylinder (h) = 8 cm
Curved surface area of cylinder = 2Πrh
= 2⋅ (22/7) ⋅ 14 ⋅ 8
= 704 sq.cm
Curved surface area of cylinder = 704 sq.cm
So, curved surface area of cylinder is 704 sq.cm
Check out:







Comments