Area of Square: Formula & How to Find Area of Square?

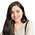
Muskan Shafi Education Content Expert

Education Content Expert

Area of Square is the region or space occupied inside the boundary of a Square. It is defined as the number of square units needed to fill a square.

Square is a two-dimensional closed shape with 4 equal sides and 4 equal angles.
It is a quadrilateral whose all angles measure 90^o.
Examples of squares include Chessboard, Tiles, Cushions, etc.

Area of Square is equal to the product of the length of its two sides. Area of a Square Formula is given as

Area of Square = Side × Side = S²

The common units used to measure the area of square are square meters (m²), square feet (ft²), square inch (in²), and square cm (cm²). Area of square can also be calculated by using other dimensions, such as the diagonal and the perimeter of a square.

Table of Content

What is Square?
What is Area of Square?
Area of a Square Formula
Area of a Square Using Diagonals
How to Find Area of a Square?
Things to Remember
Sample Questions

Key Terms: Area of Square, Area of a Square Formula, Square, Quadrilateral, Perimeter, Diagonal, Pythagoras Theorem, Angles

What is Square?

[Click Here for Sample Questions]

Square is a quadrilateral that has four equal sides. It is a closed two-dimensional shape in which all four sides are equal and parallel to each other. The four sides of the square form the four equal 90^oangles at the vertices.

Thus, a Square is defined as a Quadrilateral that has the following properties:

All four sides of a square are equal to each other.
The opposite sides of a square are parallel to each other.
All the angles of a square are equal.
Each interior angle of a square is 90°.
Diagonals of a square bisect each other at 90°.
The diagonals of a square are equal.

What is a Square?

Square

Squares are commonly found in numerous objects and around us in daily life. Some examples of square-shaped items include a Bread Slice, Chessboard, Photo Frame, Pizza Box, etc.

Read More:

Relevant Concepts
Construction of Square	Square Formula	Difference between Square and Rectangle
Area Perimeter Formula	Difference Between Area and Perimeter	Area Formula

What is Area of Square?

[Click Here for Sample Questions]

Area of Square is a measure of the space or region occupied within the boundaries of a square.

It is equal to the product of the length of its two sides.
Since it is the product of its two sides, the units of the area of square are given in square units.
The units of area of square are square meters (m²), square cm (cm²), square feet (ft²), square inch (in²), etc.

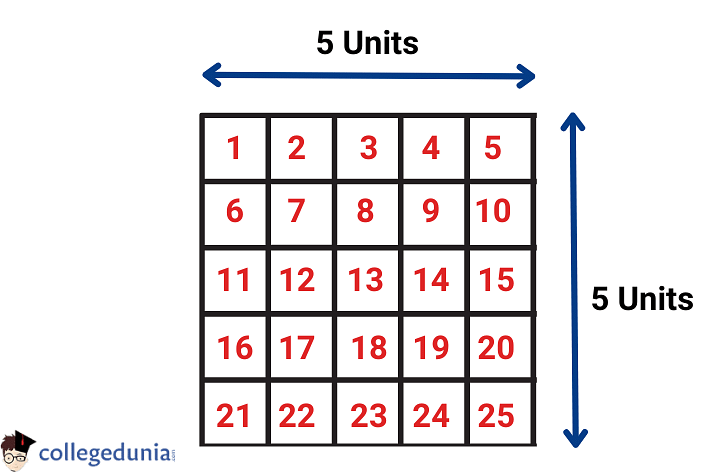
Consider the square given below. The side of the given square is 5 units.

Area of Square

Area of Square

According to the definition of the area of square, it is the product of its sides. Thus, multiplying the sides, we get

Area of Square = Side × Side = 5 × 5 = 25 Square Units

Thus, the area of the given square is 25 square units as it has occupied a total of 25 short squares.

Perimeter and Area

What is Area?

Area in Mathematics is the amount of space taken up by a 2D object or Shape.
Area is measured in "square" units.

What is Perimeter?

Perimeter in Mathematics is the total length of the boundary of an object or shape.
It is the sum total of all the sides of a given shape.

Area of a Square Formula

[Click Here for Sample Questions]

Area of Square is the product of the two sides of the square. Area of a Square Formula is given as:

Area of Square = Side × Side = S²

Since, all the sides of a square are equal, the area of a square can be found by squaring the number representing the value of the side of the square.

Solved Example

Example: What will be the Area of a Square of side 6 cm?

Solution: The side of the square is given as 6 cm.

Using the Area of a Square Formula,

Area of Square = Side x Side = S²

Substituting the value of the side, we get

Area of Square = 6 x 6 = 36 cm²

Thus, the area of the given square is 36 cm².

Read More: Understanding Quadrilaterals MCQs

Area of Square Using Diagonals

[Click Here for Sample Questions]

Area of a Square can also be calculated with the help of the Diagonals of the square. Area of Square using Diagonals is calculated using the formula:

Area of Square = Diagonal²/2

Area of Square Formula using Diagonals can be derived using the Pythagoras Theorem. Here is the derivation of the Area of the Square Formula using Diagonals:

Assume a square of sides “S” units and diagonal “d” units.

Area of Square Using Diagonals

Area of Square Using Diagonals

Applying the Pythagoras theorem, we have:

d² = S² + S²

d² = 2S²

d = √2S

S = d/√2

Substitute the value of the side in the Area of a Square Formula,

Area = S² = (d/√2)² = d²/2.

Thus, the Area of a Square Formula using Diagonals is equal to d²/2.

Read More: Construction of Quadrilaterals

How to Find Area of a Square?

[Click Here for Sample Questions]

In order to understand how to find the Area of a Square, given below are a few solved examples in different cases:

(I) Area of Square When Side of a Square is Given

Example: Find the area of a square park whose side is 80 feet.

Solution: It is given that the Side of Square Park is 80 ft.

Using the Area of a Square Formula,

Area of Square = Side x Side = S²

Area of Square Park = 80² = 80 × 80 = 6400 ft²

Thus, the area of a square park whose side is 80 ft is 6400 ft².

(II) Area of Square When Diagonal of a Square is Given

Example: What will be the area of a square park whose diagonal is 12 feet?

Solution: It is given that the Diagonal of Square Park is 12 ft.

Using the Area of a Square Formula Using Diagonals:

Area of Square using Diagonals = d²/2

Area of Square Park = (12 × 12)/2 = 72 ft²

Therefore, the area of a square park with a diagonal of 12 m is 72 ft².

(III) Area of Square When Perimeter of Square is Given

Example: Find the area of a square park whose perimeter is 280 ft.

Solution: It is given that the Perimeter of Square Park is 280 ft.

Perimeter of Square = 4 × Side

4 × Side = 280

Side = 280/4 = 70 ft

Substituting the value of the side in the Area of a Square Formula, we get

Area of Square = Side x Side = S²

Area of Square Park = 70² = 70 × 70 = 4900 ft²

Thus, the area of a square park whose perimeter is 280 ft is 4900 ft².

Check More:

Related Topics
Area of a Triangle	Area of Polygons	Area of Rectangle
Geometry Formula	Difference between Area and Volume	Area of a Circle

Things to Remember

Square is a quadrilateral in geometry with four equal sides.
It is a regular polygon with four equal angles that measure 90° each.
The opposite sides of a square are parallel and its diagonals bisect each other at 90°.
Area of Square is the measure of the amount of space occupied within a square.
Area of a Square Formula is Area of Square = Side x Side = S².
Area of a Square using Diagonals is Area of Square = d²/2
Perimeter of Square is the total length of its boundary.
Perimeter of a Square is given as Perimeter of Square = (4 × Side).

Sample Questions

Ques. Calculate the area of a square with a 100 cm perimeter. (3 Marks)

Ans. The Perimeter of the Square is 100 cm.

Perimeter of Square = 4 × Side

4 × Side = 100

Side = 100/4

Side = 25 cm

Put the value of the side in the Area of a Square Formula,

Area of Square = Side x Side = S²

Area of Square = 25² = 25 x 25 = 625 cm²

Thus, the square has an area of 625 cm².

Ques. What is the Area of a Square Clipboard whose side measures 120 cm? (3 Marks)

Ans. It is given that the Side of the Square Clipboard = 120 cm = 1.2 m

Using the Area of a Square Formula,

Area of Square = Side x Side = S²

Area of Square Clipboard = 120 cm × 120 cm

= 14400 sq. cm

= 1.44 sq. m

Thus, the area of the square clipboard is 1.44 sq. m.

Ques. What is Area of Square? (3 Marks)

Ans. Square is a two-dimensional closed figure with four equal sides. It is a quadrilateral that has four equal sides and four equal angles with each angle measuring 90°. Area of Square is defined as the total number of unit squares in the shape of a square. In other words, it is defined as the space or region occupied by the square. It is the product of the two sides of a square.

Area of a Square Formula is given as

Area of Square = Side x Side = S²

Ques. The side of a square wall is 75 m. Find the cost of painting it at the rate of Rs. 3 per sq. m. (3 Marks)

Ans. Given, Side of the Square Wall = 75 m

Using the Area of a Square Formula,

Area of Square = Side x Side = S²

Area of Square Wall = 75 m × 75 m = 5625 sq. m

For 1 sq. m, the cost of painting is Rs. 3.

Thus, for 5625 sq. m, the cost of painting will be

Rs. 3 × 5625 = Rs. 16875

Therefore, the cost of painting a square with a side 75 m at the rate of Rs. 3 per sq. m is Rs. 16875.

Ques. Calculate the Size of a Square Park whose Perimeter is 360 feet. (3 Marks)

Ans. It is given that the perimeter of the square park is 360 feet.

Perimeter of Square = 4 × Side

4 × Side = 360

Side = 360/4

Side = 90 ft

Substituting the value of the obtained side in the Area of a Square Formula, we get

Area of Square = Side x Side = S²

Area of Square Park = 90² = 90 x 90 = 8100 ft²

Thus, the size of a square park with a 360 feet perimeter is 8100 ft².

Ques. What is the Diagonal of a Square? (3 Marks)

Ans. Diagonal is the line stretching from one corner of a closed figure to the opposite corner through the center of the figure.

A square has two diagonals.
Diagonals of a square are equal in length.
They bisect each other at 90°.

Ques. Square tiles will be used to cover the floor of a courtyard that is 50 meters long and 40 meters broad. Each tile has a 2 m side. Calculate the number of tiles needed to cover the entire floor. (3 Marks)

Ans. According to the question,

Length of Floor = 50 m
Breadth of Floor = 40 m

Thus, the area of the floor will be calculated using the Area of a Rectangle formula,

Area of Floor = Length x Breadth = 50 m x 40 m = 2000 sq. m.

The length of each tile is 2 meters.

Thus, the area of each tile will be calculated using the Area of a Square Formula,

Area of Tile = Side x Side = 2 x 2 = 4 m

The number of tiles necessary will be calculated by multiplying the area of the floor by the area of a tile.

Number of Tiles = 2000/4 = 500 Tiles

Therefore, 500 tiles are needed to cover the entire floor which is 50 meters long and 40 meters broad.

Ques. What is the Area of a Square by using Diagonals? (3 Marks)

Ans. Diagonals of a Square are equal and bisect each other at 90°. Area of a Square using Diagoanls is calculated using the formula:

Area of Square using Diagonals = d²/2

Derivation of Area of a Square using Diagonals

The derivation of the Area of a Square using Diagonals is done using the diagram below, where 'd’ indicates diagonal and 's' indicates the square's sides.

According to the Pythagoras Theorem,

d² = s² + s²

d² = 2s²

d = √2s

s = d/√2

Put the value of the side in the Area of a Square Formula,

Area = s² = (d/√2)² = d²/2

Hence, the Area of a Square Formula using Diagonals is d²/2.

Ques. Calculate the Area of a Square Park whose diagonals are 14 feet. (3 Marks)

Ans. The diagonal of the square park is 14 feet.

Using the Area of a Square Formula Using Diagonals:

Area of Square using Diagonals = d²/2

Area of Square Park = (14 × 14)/2 = 98 ft²

Therefore, the area of a square park with a diagonal of 14 m is 98 ft².

Ques. Calculate the area of the square with a 20-meter side. (3 Marks)

Ans. The Side of the Square is given as 20 m.

Using the Area of a Square Formula,

Area of Square = Side x Side = S²

Area of Square = 20² = 20 × 20 = 400 m²

Thus, the area of a square park whose side is 20 m is 400 m².

Check-Out:

Important Study Guides
NCERT Solutions Class 6 to 12	NCERT Solutions for Class 8 Maths	NCERT Solutions for Class 8 Science
Biology Study Notes	Biology MCQs	Topics for Comparison in Physics
Physics Study Notes	Important Named Reactions	Topics with relation in physics
Comparison Topics in Biology	SI Units in Physics	Important Derivations in Physics
Physics MCQs	Formulas in Physics	Important Physics Constants and Units
Chemistry Study Notes	Comparison topics in Chemistry	Chemistry MCQs
Maths MCQs	Important Chemistry Formulas	Important Maths Formulas

Area of Square: Formula & How to Find Area of Square?

What is Square?

What is Area of Square?

Perimeter and Area

Area of a Square Formula

Solved Example

Area of Square Using Diagonals

How to Find Area of a Square?

(I) Area of Square When Side of a Square is Given

(II) Area of Square When Diagonal of a Square is Given

(III) Area of Square When Perimeter of Square is Given

Things to Remember

Sample Questions

CBSE X Related Questions

1.
AB and CD are diameters of a circle with centre O and radius 7 cm. If \(\angle BOD = 30^\circ\), then find the area and perimeter of the shaded region.

2.
If the zeroes of the polynomial $ax^2 + bx + \dfrac{2a}{b}$ are reciprocal of each other, then the value of $b$ is

3.
In a right triangle ABC, right-angled at A, if $\sin B = \dfrac{1}{4}$, then the value of $\sec B$ is

4.
In the adjoining figure, TS is a tangent to a circle with centre O. The value of $2x^\circ$ is

5.
Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

6.
Find length and breadth of a rectangular park whose perimeter is \(100 \, \text{m}\) and area is \(600 \, \text{m}^2\).

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

Area of Square: Formula & How to Find Area of Square?

What is Square?

What is Area of Square?

​Perimeter and Area

Area of a Square Formula

Solved Example

Area of Square Using Diagonals

How to Find Area of a Square?

(I) Area of Square When Side of a Square is Given

(II) Area of Square When Diagonal of a Square is Given

(III) Area of Square When Perimeter of Square is Given

Things to Remember

Sample Questions

CBSE X Related Questions

1.AB and CD are diameters of a circle with centre O and radius 7 cm. If \(\angle BOD = 30^\circ\), then find the area and perimeter of the shaded region.

2.If the zeroes of the polynomial $ax^2 + bx + \dfrac{2a}{b}$ are reciprocal of each other, then the value of $b$ is

3.In a right triangle ABC, right-angled at A, if $\sin B = \dfrac{1}{4}$, then the value of $\sec B$ is

4.In the adjoining figure, TS is a tangent to a circle with centre O. The value of $2x^\circ$ is

5.Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

6.Find length and breadth of a rectangular park whose perimeter is \(100 \, \text{m}\) and area is \(600 \, \text{m}^2\).

Similar Mathematics Concepts

Comments

SUBSCRIBE TO OUR NEWS LETTER

Perimeter and Area

1.
AB and CD are diameters of a circle with centre O and radius 7 cm. If \(\angle BOD = 30^\circ\), then find the area and perimeter of the shaded region.

2.
If the zeroes of the polynomial $ax^2 + bx + \dfrac{2a}{b}$ are reciprocal of each other, then the value of $b$ is

3.
In a right triangle ABC, right-angled at A, if $\sin B = \dfrac{1}{4}$, then the value of $\sec B$ is

4.
In the adjoining figure, TS is a tangent to a circle with centre O. The value of $2x^\circ$ is

5.
Given that $\sin \theta + \cos \theta = x$, prove that $\sin^4 \theta + \cos^4 \theta = \dfrac{2 - (x^2 - 1)^2}{2}$.

6.
Find length and breadth of a rectangular park whose perimeter is \(100 \, \text{m}\) and area is \(600 \, \text{m}^2\).