
Jasmine Grover Content Strategy Manager
Content Strategy Manager
A parabola is derived from conic sections. A section that is cut off, in various ways, from a right circular cone by a planne forms a conic section. The position of the cutting plane determines the shape of the coic section. The section of the right circular cone which is cut by a plane parallel to the generator of the cone is known as a parabola.

A conic section analytically can be defined as the locus of a point, which moves in such a way that its distance from some fixed point is in a constant ratio to the distance from a fixed straight line, that is not passing through the fixed point. Let us recall some important points about conic sections:
- The focus refers to the fixed point.
- The straight line that is fixed is known as the directrix.
- The constant ratio is known as eccentricity and is denoted by the letter 'e'.
- When the eccentricity is unity i.e. e = 1, the conic formed is called a parabola; when e < 1, the conic formed is called an ellipse: and when e > 1, the conic is called a hyperbola. When e = 0, the conic formed is called a circle and for e = ∞ , a pair of straight lines are formed.
Standard Equation of a Parabola
Parabola is defined as the locus of points equidistant from a fixed point (called focus S) and a fixed-line (called directrix MZ).
-
For horizontal parabola
- Let us consider
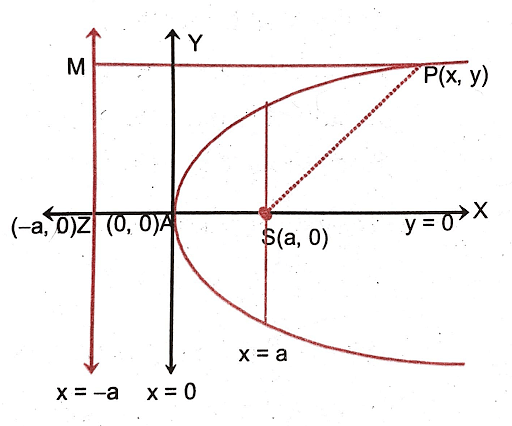
- Origin (0,0) as the parabola's vertex A,
- Two equidistant points S(a,0) as focus, and Z(- a,0) as a directrix point,
- P(x,y) as the moving point.
- Let us now draw SZ perpendicular from S to the directrix. Then, SZ will be the axis of the parabola.
- The centre point of SZ i.e. A will now lie on the locus of P, i.e. AS = AZ.
- The x-axis will be along the line AS, and the y-axis will be along the perpendicular to AS at A, as in the figure.
- By definition PM = PS
=> MP2 = PS2
- So, (a + x)2 = (x - a)2 + y2.
- Hence, we can get the equation of horizontal parabola as y2 = 4ax.
-
For vertical parabola
- Let us consider

- Origin (0,0) as the parabola's vertex A
- Two equidistant points, S(0,b) as focus and Z(0, -b) as a directrix point
- P(x,y) as any moving point
- Let us now draw a perpendicular SZ from S to the directrix.
- Then SZ will be the axis of the parabola. Now, the midpoint of SZ i.e. A, will lie on P’s locus i.e. AS=AZ.
- The y-axis will be along the line AS, and the x-axis will be perpendicular to AS at A, as shown in the figure.
- By definition PM = PS
=> MP2 = PS2
So, (b + y)2 = (y - b)2 + x2
- As a result, the vertical parabola equation is x2= 4by.
Discover about the Chapter video:
Conic Sections Detailed Video Explanation:
General Equation of any Parabola
Let us now find out the equation of a parabola when the directrix is any line and the focus is any point.
Let us assume (h,k) is the focus S and the line Ix + my + n = 0 is the equation of the directrix ZM of the parabola. Let us take (x,y) as the coordinate of any point P on the parabola. The relationship PS = distance of P from ZM thus yields -
(x- h)2 + (y - k)2 = (Ix + my + n)2 / (l2+ m2)
=› (Ix - my)2 + 2gx + 2fy + d = 0
This is the general equation of any parabola. The second-degree terms in the equation of the parabola constitute a perfect square. The converse will be also true, i.e. If the second-degree components in an equation form a perfect square, the equation represents a parabola, unless the equation represents two parallel straight lines.
Note: The general second degree polynomial function i.e. ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a parabola if Δ ≠ 0 and h2 = ab (where Δ = abc+ 2fgh - af2 - bg2 - ch2).
Latus Rectum of a Parabola
Latus rectum is known as the chord that passes through the focus and is perpendicular to the axis of the parabola.
We will now put x = a as the latus rectum that passes through focus (a,0) to find the endpoints of latus rectum LL' of the parabola y2 = 4ax.
Therefore we have,
y2 = 4a2
=> y= ±2a
As a result, the endpoints are (a, 2a) and (a, -2a).
Also LSL' = |2a - (-2a)| = 4a = length of double ordinate through the focus S.
Note: When the latus rectum of two parabolas is equal, then these parabolas are said to be equal.

Important points to remember about the standard parabolas
| Form of the parabola | y2 = 4ax (Horizontal) | x2 = 4by (Vertical) |
| Vertex | (0,0) | (0,0) |
| Focus | (a,0) | (0,b) |
| Equation of the Directrix | x = -a | y = -b |
| Equation of the axis | y = 0 | x = 0 |
| Tangent at the vertex | x = 0 | y = 0 |
| Equation of latus rectum | x = a | y = b |
| Length of latus rectum | |4al | |4bl |
| End points of latus rectum | (a,2a) & (a,-2a) | (2b,b) & (-2b,b) |
Note:

- The following transformations can be used to interchange the points and lines of two parabolas -
x ↔ y, a ↔ b, (α,β) ↔ (β,α )
- if a > 0 & a < 0 then the parabola will be forward opening and backward opening respectively.
- if b > 0 & b < 0 then the parabola will be upward opening and downward opening respectively.
Important points to remember about any shifted Parabola
The forms of the horizontal and vertical parabolas having the vertex at (h,k) can be obtained by shifting the origin at (h,k).
| Form of the parabola | (y-k)2 = 4a(x-h) | (x-h)2 = 4b(y-k) |
| Vertex | (h, k) | (h, k) |
| Focus | (a+h,k) | (h,b+k) |
| Equation of the Directrix | x = -a+h | y = -b+k |
| Equation of the axis | y = k | x = h |
| Tangent at the vertex | x = h | y = k |
| Equation of latus rectum | x = a+h | y = b+k |
| Length of latus rectum | | 4a | | | 4b | |
| End points of latus rectum | (a+h, 2a+k) & (a+h, -2a+k) | (2b+h, b+k) & (-2b+h, b+k) |
Parametric Form of a Parabola
Let us assume that the tangent equation to the parabola y2 = 4ax-- (i)
is y = mx + c …..(ii)
The equation (mx + c)2 = 4ax gives us the x-cordinate of the points of intersection of (i) and (ii).
However, the criterion for the straight line (ii) is that it must meet the parabola at coinciding locations. Hence, discriminant should be zero
=> (mc - 2a)2 = m2c2
=> c = a/m
As a result, y = mx + a/m gives us the equation of the tangent to the parabola y2 = 4ax, where ‘m’ can take any value.
So, the equation (mx + c)2 = 4ax has now become (mx - a/m)2 = 0
=> x = a/m2
and y2 = 4ax
=> y = 2a/m
Thus the tangent y = mx + a/m contacts the parabola at these point - (a/m2, 2a/m)
Taking 1/m= t where t is a parameter, i.e., it can vary from point to point on any curve. The parabola y2 = 4ax can be represented in parametric form by the co-ordinate (at2,2at) and we refer to it as point ‘t' on the parabola.
Focal Chord of a Parabola

Any chord which passes through the focus is known as a focal chord of the parabola.
Let y2 = 4ax be the equation of a parabola and point P be at (at2,2at) on the parabola. Let us assume that the coordinates of the extremity Q of the focal chord passing through point P are (at12,2at1).
Then, PS and SQ (where S(a,0) is the focus), have same slopes
=> 2at - 0/at2 - a = 2at1 - 0/at12 - a
=> tt12 - t = t1t2 - t1 => (tt1 + 1) (t1 - t) = 0
So, t1= -1/t, that means the point Q can be written as (a/t2,-2a/t).
So, for simplicity, the extremities of any focal chord of the parabola y2 = 4ax can be assumed as the points t and -1/t.
Focal Distance of a Point

A point P on the parabola, y2 = 4ax has a focal distance of PS, which is the distance between the point P and the focus S. So, the focal distance of P becomes - y2 = 4ax
=> PM = ZN = PS = AN + AZ = a + x
or
=> PS = a+ at2 = a(1 + t2)
Position of any point with respect to a Parabola

Consider the parabola y2 = 4ax. Let us assume (x1,y1) is any given point P on the parabola and y12 - 4ax1 = 0, then that point will lie on the parabola. However, when y12-4ax1 ≠ 0, y-coordinate PM is plotted to meet the curve at point L.
Now, point P would lie outside of the parabola if -
LM < PM, that is, PM2 - LM2 > 0.
Now, PM2 = y12 and LM2 = 4ax1 by reference to the coordinates of point ‘L’ which satisfies the equation of the given parabola. As a result, the condition for point P to lie outside of the parabola becomes y12 - 4ax1 > 0.
In the same way, we can conclude that the condition for point P to lie inside of the parabola, is y12 - 4ax1 < 0.
Tangent to a Parabola
A line that touches any curve at exactly one point is called a tangent to that curve.
The tangent at the point (x1, y1)

Let us assume the equation of the standard parabola is y2 = 4ax. As a result, the value of dy/dx at point P(x1,y1) is 2a/y1 and thus the equation of the tangent at P is
y - y1= 2a/y1(x-x1)
i.e. yy1 = 2a(x-x1) + y12
=> yy1= 2a(x+x1)
In other words, we can write the equation of chord joining the points P (x1,y1) and Q (x2,y2) on the parabola y2 = 4ax. Equation of the chord is
=> (x-x1)/(x2 - x1)= (y- y1)/(y2 - y1)
(x-x1)/(x2-x1)= (y-y1)(y2+y1)/ y22-y12 = (y-y1)(y2 + y1)/ 4a(x2 - x1) or 4a(x -x1) = (y -y1) (y2 + y1) .
When the two points P and Q tend to coincide, y2 → y1 and then the line PQ will be the tangent to the given parabola. Its equation is 4a(x - x1) = (y - y1)(2y1) or yy1 = 2a(x + x1)
Tangent in terms of m
Let us assume that the tangent equation to the parabola y2 = 4ax...(i)
is y = mx + c.....(i)
The abscissa of the intersection points of (i) and (ii) are given by the equation:
(mx+c)2= 4ax
However, the criterion for the straight line (ii) to contact the parabola is that it must do so at coinciding locations.
=> (mc - 2a)2 = m2c2.... (iii)
=> c = a/m
Hence, y = mx + a/m is a tangent to the parabola y2 = 4ax, for all the possible values of ‘m’.
Now, the equation (mx +c)2 = 4ax becomes (mx - a/m)2 = 0 .
x = a/m2 and
y2 = 4ax
=> y = 2a/m
As a result, the tangent y = mx + a/m has (a/m2,2a/m) as contact point.
Tangent at the point ‘t’
The tangent equation at ‘t' is ty = x + at2 .
(at1t2, a(t1+t2)) is the point of intersection of the tangents at 't1' and 't2' .
Tangent equations from an External Point
Let y2 = 4ax be the equation of a parabola and (x1,y1) be any external point P . Now, the equation of the tangents can be written as :
SS1 = T2, where S = y2 - 4ax, S1 = y12 - 4ax1, T = yy1 - 2a(x + x1).
PQ is the chord of contact of the tangents if the tangents from the exterior point (x1,y1) touch the parabola at P and Q.
Chord of Contact
The equation for the chord of contact of the tangent that is drawn from a point (x1,y1) to a parabola y2 = 4ax is T = 0, i.e. yy1 - 2a(x+x1) = 0.
Note: The equation for the chord of the parabola y2= 4ax with its midpoint at (x1,y1) is T=S1
i.e. yy1 - 2a(x + x1) = y12 - 4ax1 .
or
yy1-2ax = y12-2ax
Normal to a Parabola
A line that is perpendicular to the tangent of any curve at its point of contact to the curve, is called a normal to that particular curve.
Normal at the point (x1,y1)
The equation of the tangent at the point (x1,y1) is yy1 = 2a( x + x1).
Since,
Slope of the tangent = 2a/y1
The slope of the normal is -y1/2a.
Also, it will pass through the point (x1,y1)
As a result, the equation of the normal at a point is (y - y1) = -y1/2a(x - x1)......(i)
Normal in terms of m
In equation (i), put -y1/2a = m so that y1 = -2am and x1 = y12/4a = am2, then the equation becomes
y = mx - 2am - am3…….(ii)
where, ‘m’ is the slope. The equation (ii) is the equation of the normal at the point (am2,-2am) of the parabola. am3
Note:
- If this normal passes through any point (h, k), then k = mh-2am-am3 for any given parabola and any given point (h,k), then this cubic variable in ‘m' will have three roots, namely m1, m2, and m3, which means that three normals can be drawn from (h,k) to the parabola whose slopes are m1, m2, and m3 respectively.
For this cubic function, we have
m1 + m2 + m3 = 0, m1m2 + m2m3 + m3m1 = (2a-h) / a,
m1m2m3 = -k/a.
If we add an extra condition to the normals drawn from any point (h, k) to a specified parabola, such as y2 =4ax, we may get the locus of the parabola by elimination of m1, m2, and m3 from the four relations between them.
- Because the sum of the roots, m1, m2, and m3, is zero; the sum of the ordinates of the feet of the normals from any given position is also zero. These points are known as Co-Normal Points.
Normal at the point ‘t’
y = -tx + 2at + at3 is the normal which is perpendicular to the tangent at the point (at2,2at)
Note:
- If the normal at t1 point meets the parabola again at point t2, then t2= -t1 - 2/t1
- Point of intersection of the normals to the parabola y2 = 4ax at (at12,2at1) and (at22,2at2) is (2a + a (t12 + t22 + t1t2), - at1t2(t1+ t2)).
Important Topics for JEE MainAs per JEE Main 2024 Session 1, important topics included in the chapter parabola are as follows:
Some memory based important questions asked in JEE Main 2024 Session 1 include: 1. Shortest distance between the parabola y2 = 4x and x2 + y2 - 4x-16y + 64 = 0 is equal to? |
Sample Questions of Parabola
Question: . Find the parabola's vertex, axis, directrix, tangent at the vertex, and length of the latus rectum for the given parabola: 2y2 + 3y - 4x - 3 = 0. (2 marks)
Solution: The given equation can be re-written as (y + ¾)2 = 2(x+33/32)
Whose form resembles y2 = 4ax
Hence the vertex is (-33/32 , -¾)
The axis is y + 3/4 = 0 => y = -3/4
The directrix is x + a = 0
=> x + 33/32 + ½ = 0 => x = -49/32
At the vertex, the tangent is : x + 33/32 = 0 => x = -33/32
Latus rectum = 4a = 2.
Question: Find the equation of the parabola whose focus is (3,-4) and directrix, x - y + 5 = 0. (2 marks)
Solution: Let as assume P(x, y) as any point on the parabola. Then
=> √(x-3)2 + (y+4)2 = |x-y+5|/√1+1
=> (x-3)2 + (y+4)2 = (x-y+5)2/2
=> x2 + y2 + 2xy - 22x + 26y + 25= 0
=> So, (x+y)2 = 22x - 26y - 25
Question: Find the length of the latus rectum of the parabola y2 = 4ax if the line 2x + 3y = 1 touches it. (2 marks)
Solution: Tangent equation to y2 = 4ax is written as :
=> y = mx + a/m
=> m2x - my+ a =0
Comparing this equation with the given tangent (2x + 3y - 1 = 0), we find
m2/2 = -m/3 = a/-1
=> m= -? , a = m/3 = -2/9
Hence, the length of the latus-rectum
= 4*a = 8/9, (Ignore the negative sign)
Question: Prove that there are two tangents to the parabola y2 = 4ax passing through any given point (x1,y1). (3 marks)
Solution: The equation to any tangent is y = mx + a/m……(i)
When this line passes through the fixed point (x1,y1), we can write :
y1 = mx1 + a/m, i.e. m2x1 - my1 + a = 0……..(ii)
It forms a quadratic equation that gives us two values of m (real or imaginary). Substituting each value of ‘m’ we can get two different possible tangents, each corresponding ‘m’.
- The roots of (ii) are real and different if y2 - 4ax1 > 0, which means if the point (x1,y1) lies outside the curve.
- The roots are equal, if y12 - 4ax1 = 0, that means if the point (x1,y1) lies on the curve. In this case, the two tangents merge into one. Now the two roots will be imaginary when y12 - 4ax1< 0, which means the given point (x1, y1 ) lies within the curve.
Question: Deduce the equations of the normals to the parabola, represented by y2 = 4ax at the extremities of its latus rectum. If the normals meet the given parabola again at points P and Q, prove that PQ = 12a. (2 marks)
Solution: End points of the latus rectum are : (a,2a) and (a,-2a). The equations of the normals to the parabola at these points are (put t = 1 and t = -1) :
=> y + x = 3a
and
=> y - x = 3a.
Now, both of the lines will meet the parabola again at points P(9a,-6a) and Q(9a,6a) , respectively
Hence, PQ = 6a+6a
= 12a





Comments