
Content Curator
Ellipse is a plane curve that surrounds two focal points, in such a way that for all points on the curve, the sum of two distances to the focal point is a constant. It resembles a circle, which is a special type of ellipse in which both the focal points are the same.
- An ellipse is a closed plane curve, obtained by a point that moves in such a way that the sum of their distances from any two fixed points remains a constant.
- A plane section from a right circular cone is a closed curve.
- The fixed points are called ‘foci’ which are surrounded by the curve.
The equation of ellipse is given by:
| \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) |
- The major axis and minor axis define the area of an oval-shaped ellipse.
- The eccentricity that demonstrates the elongation of the ellipse is denoted by the variable “e”.
- Ellipse is part of the conic section. For example, the Parabola and the Hyperbola
- Parabola is open in shape and unbounded. Generally, an ellipse is defined by its equation.
| Table of Content |
Key Terms: Ellipse, Standard Equation, Parabola, Hyperbola, Conic Section, Eccentricity, Locus, Major Axis, Minor Axis, Latus Rectum
Ellipse Meaning
[Click Here for Sample Questions]
An ellipse is the set of all points on an X-Y plane, whose distance from two fixed points (known as foci) adds up to a value that remains constant.
- Ellipse is the part of the conic section that is produced when a plane cuts the cone at an angle with the base.
- It forms a circle when the cone is intersected by the plane, parallel to the base.
- The shape of an ellipse is like an oval or flattened circle.
- A closed curve which contains points whose distances from each of two fixed points sum up to the same value is simply the ellipse definition.
- The fixed point in an ellipse is called the Focus and is signified by S.
- The constant ratio “e” is known as the Eccentricity, while the fixed line is the Directrix (d) of the ellipse.

What is Ellipse?
Major and Minor Axis
The following two-axis along the x and y-axis define the ellipse.
- Major Axis: The longest diameter of the ellipse is known as the major axis. It crosses through the centre from one end to another, at the broader part of the ellipse.
- Minor Axis: The shortest diameter of the ellipsis is known as the minor axis, which crosses through the centre at the narrowest part.

Major and Minor Axis
Discover about the Chapter video:
Conic Sections Detailed Video Explanation:
Parts of Ellipse
[Click Here for Previous Year Questions]
The parts of an ellipse include:
- Focus: The ellipse has two foci, with coordinates F(c, o), and F'(-c, 0). The distance between the foci is equivalent to 2c. The foci of ellipse are simply known to be the two reference points which help in drawing the ellipse.
- Center: The centre of an ellipse is the midpoint of the line which joins the two foci.
- Major Axis: The length of the major axis in an ellipse is equal to 2a units, with the end vertices of the major axis as (a, 0), (-a, 0) respectively.
- Minor Axis: The length of the minor axis in an ellipse is equal to 2b units, with the end vertices of the minor axis as (0, b), and (0, -b) respectively.
- Latus Rectum: The latus rectum of an ellipse can be defined as a line which is drawn perpendicular to the transverse axis in an ellipse. It passes via the foci of the ellipse. The length of the latus rectum is 2b2/a.
- Transverse Axis: The line which passes via the two foci and the centre of the ellipse is known as the Transverse Axis.
- Conjugate Axis: Conjugate Axis is the line which passes via the centre of the ellipse and is also perpendicular to the transverse axis.
- Eccentricity: Eccentricity is the ratio of the distance from the centre of the ellipse to either the focus or the vertices of the ellipse.
Also Read:
Eccentricity of Ellipse
[Click Here for Sample Questions]
The ratio of the distance from the centre of the ellipse from either the focus or the vertices of the ellipse is known as the eccentricity of the ellipse.
The eccentricity of an ellipse is equal to:
| e = c/a |
Where,
- c = focal length
- a = length of the semi-major axis
Since the value of c ≤ a, the eccentricity (e) is always greater than the value of 1 in the case of an ellipse.
Also,
⇒ c2 = a2 – b2
Thus, eccentricity can be given as:
⇒ e = √(a2 – b2)/a
Hence,
| e = √[(a2 – b2)/a2] e = √[1-(b2/a2)] |
Properties of Ellipse
[Click Here for Previous Year Questions]
Some of the important properties of an ellipse are listed below:
- There are two focal points in an ellipse, which are also known as ‘foci’.
- The fixed distance is called a Directrix.
- The Eccentricity of an Ellipse lies between 0 and 1. Thus, 0 ≤ e < 1.
- The total sum of each distance from the locus of an ellipse to the two focal points is constant .
- Ellipse has one major axis, one minor axis, and a centre.
Read More:
Equation of Ellipse
[Click Here for Sample Questions]
When the centre of the ellipse is at the origin that is equal to (0,0) and the foci are on the x-axis and y-axis, then the general equation of ellipse can easily be derived as:
| \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \) |
An ellipse is a closed structure in a two-dimensional plane, so it covers a region in a 2D plane, and this bounded region of the ellipse is called an area. The structure of the ellipse is different from the circle, Hence the formula of its area will also be different.
Formula for Equation of an Ellipse
The equation of an ellipse formula demonstrates an ellipse in the algebraic form. The formula to find the equation of an ellipse can be denoted by:
- Equation of the ellipse with centre at (0,0) : x2/a2 + y2/b2 = 1
- Equation of the ellipse with centre at (h,k) : (x-h)2 /a2 + (y-k)2/ b2 = 1
Solved ExampleQues: If the length of the major axis is equal to 8cm and the minor axis is equal to 7cm, find the area of the ellipse. (2 marks) Ans: Given: The length of the major axis is 8cm The length of the minor axis is 7cm By the formula of area of an ellipse, we know that: Area of the ellipse = π x Major axis x Minor axis Area of the ellipse = π x 8 x 7 Area of the ellipse = π56 As we know the value of π is = 22/7 Area= 22/7 x 56 Therefore, the area of the ellipse is 176 cm2 |
Derivation of Ellipse Equation
[Click Here for Previous Year Questions]
As per the derivation, follow the figure below:
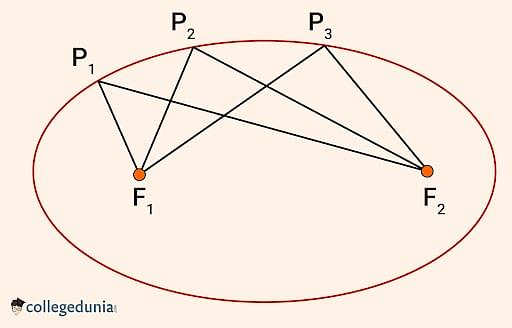
Ellipse Equation Derivation
The given figure demonstrates an ellipse with P1F1 + P1F2 = P2F1 + P2F2 = P3F1 + P3F2 as a constant. This constant is known to be greater than the distance between the two foci.
In case both the foci are joined by means of a line segment, the mid-point of the line segment which helps join the foci is referred to as the center, while O represents the centre of the ellipse.
Thus, the proof of ellipse equation is:
Sum of distances of B from F1 = F1B + F2B = F1O + OB + F2B (According to the Figure below)
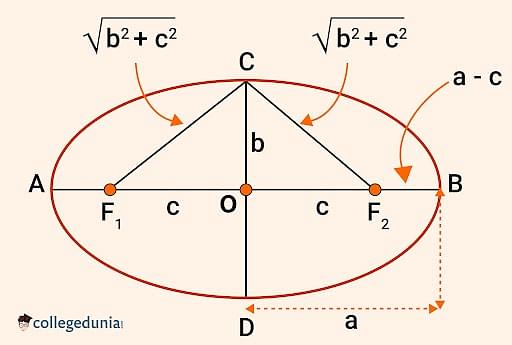
Ellipse Equation Proof
Hence,
⇒ c + a + a – c = 2a
Sum of distances from point C to F1 = F1C + F2C
Thus,
⇒ F1C + F2C = √(b2 + c2) + √(b2 + c2) = 2√(b2 + c2)
As per the definition of ellipse, it can be said that:
2√(b2 + c2) = 2a
⇒a = √(b2 + c2)
⇒ a2 = b2 + c2
⇒ c2 = a2 – b2

Constructing an Ellipse
For Special CasesIn case of special cases,
|
Area of Ellipse
[Click Here for Sample Questions]
We calculate the area of a circle by its radius, but the area of the ellipse depends on the length of the major axis and minor axis.
As we know the area of the circle is = πr2
Hence, the area of ellipse is = \(\pi\ \times\ Major\ Axis\ \times\ Minor\ Axis\)
Thus, the area of ellipse formula is:
| Area of Ellipse = \(\pi.a.b\) |
Where the variables a and b are the length of the major axis and minor axis.
Perimeter of Ellipse
[Click Here for Previous Year Questions]
The perimeter of an ellipse can be defined as its total distance outlined by its outer boundary.
- In case of a circle, the circumference can be easily found because the distance from the centre to any point of the locus of the circle is the same.
- This distance is known as the Radius.
- But in the case of an ellipse, the two axes, major and minor are seen to cross via the centre and simultaneously intersect.
Thus, an approximation formula is used to determine the perimeter of an ellipse:
⇒ \(\begin{array}{l}p \approx 2 \pi \sqrt{\frac{a^{2}+b^{2}}{2}}\end{array}\)
Here,
- a = length of the semi-major axis
- b = length of the semi-minor axis
Uses of EllipseThe ellipse is one of the four conic sections created by slicing a cone with a plane. The others are the parabola, the hyperbola, and the circle.
|
Standard Equation of Ellipse
[Click Here for Sample Questions]
An ellipse has two standard equations. These equations, in the case of each ellipse, are based on the transverse axis and the conjugate axis.
- The standard equation of the ellipse \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \) contains the transverse axis in form of the x-axis, while the conjugate axis as the y-axis.
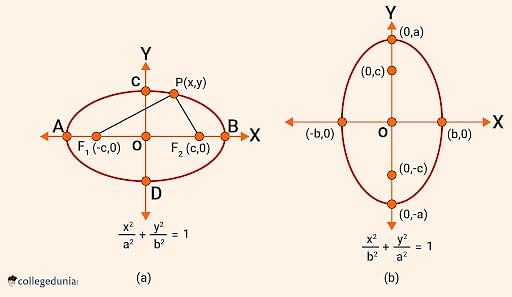
Ellipse Standard Equation
- Another standard equation in the case of an ellipse is \(\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1 \), with the transverse axis as the y-axis, while the conjugate axis here as the x-axis.
Graph of Ellipse
[Click Here for Previous Year Questions]
To make a graph of Ellipse:
Step 1
The ellipse is first is going to intersect the x-axis in points A (a, 0), A'(-a, 0) while the y-axis in points B(0, b), B'(0, -b).
Step 2
The ellipse vertices are A(a, 0), A'(-a, 0), B(0,b), B'(0,-b).
Step 3
Because the ellipse is symmetric at its coordinate axes, the ellipse comes with two foci S(ae, 0), S'(-ae, 0).
Step 4
The ellipse is known to be a closed curve which lies within the rectangle bordered by the four lines x = ±ax and y = ±by
Step 5
The segment AA′ of length 2a is known as the major axis, while the segment BB′ of length 2b is known as the minor axis.
Read More:
Important Topics for JEE MainAs per JEE Main 2024 Session 1, important topics included in the chapter ellipse are as follows:
Some memory based important questions asked in JEE Main 2024 Session 1 include:
|
Things to Remember
- An ellipse in math can be defined as a locus of points in a plane, such that its distance from a fixed point has a constant ratio “e” to the distance coming from a fixed-line.
- The ellipse equation is = \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \).
- The ellipse perimeter is = \(\begin{array}{l}p \approx 2 \pi \sqrt{\frac{a^{2}+b^{2}}{2}}\end{array}\).
- The ellipse area is = \(\pi.a.b\).
Previous Year Questions
- The length of the common chord of the ellipse…..[BITSAT 2007]
- The locus of the point of intersection of the tangents….[KCET 2010]
- The equations of the two tangents from (-5, - 4) to the circle...[KCET 2012]
- The eccentricity of the ellipse...[KCET 2007]
- The tangents drawn at the extremities of a focal chord...[KCET 2008]
- Two circles centered at (2, 3) and (5,6) intersect each other...[KCET 2010]
- The length of transverse axis is equal to...[KCET 2015]
- Equation of the circle centered at (4, 3) touching the circle….[KCET 2010]
- The points (1,0), (0,1), (0,0) and (2k, 3k) = 0 are concyclic... [KCET 2010]
- For the parabola y2 = 4x, the point P whose focal distance is 17, is….[KCET 2009]
Sample Questions
Ques: What is Auxilary Circle? (1 mark)
Ans: Auxilary circle is a kind of circle that is drawn on the major axis of the ellipse. The equation of an auxiliary circle to the ellipse is x2 + y2 = a2.
Ques: What is the shape of the ellipse? (1 mark)
Ans: The shape of an ellipse is like an oval or a flattened circle. A set of all points in a plane, the sum of whose distance from two fixed points, called the foci, is a constant. A circle is a special type of an ellipse having both focal points as same, the center. In geometry, an ellipse is defined as a two-dimensional shape, defined along its axes.
Ques: How ellipses are used in real life? (1 mark)
Ans: Ellipses can be used to represent many real-life situations including orbits of planets, satellites, moon, and comets and the shape of boat keels, and some airplane wings. A medical device called a lithotripter uses an elliptical reflector to break up kidney stones by generating sound waves.
Ques: What is the difference between the area of the circle and the ellipse? (2 marks)
Ans: We calculate the area of a circle by its radius, but the area of the ellipse depends on the length of the major axis and minor axis.
As we know the area of the circle is = πr2
Hence, the area of the ellipse is = π x Major axis x Minor axis
Area of the ellipse = π.a.b
Here, variables a and b are the length of the major axis and minor axis.
Ques: What are the properties of the ellipse? (3 marks)
Ans: Some of the properties of an ellipse are:
- There are two focal points of an ellipse known as the foci.
- The fixed distance is called a directrix.
- The eccentricity of the ellipse lies between 0 to 1.0 ≤e <1.
- The total sum of each distance from the locus of an ellipse to the two focal points is constant
- Ellipse has one major and one minor axis and a center.
Ques: What are the major axis and minor axis? (1 mark)
Ans: The major axis is known to be the longest diameter of the ellipse, going through the centre from one end to the other end, at the broad part of the ellipse.
The minor axis is known as the shortest diameter of the ellipse, which crosses through the centre at the narrowest part.
Ques: What are the values of 'a' and 'b' in the given equation of an ellipse: 16x2 + 25y2 = 1600? (3 marks)
Ans: In order to obtain the values of 'a' and 'b', the given equation is to be written in the standard form
Thus, we have to divide the given equation of an ellipse: 16x2 + 25y2 = 1600 by 1600.
Hence,
= \(\frac{{x^2}}{100} + \frac{{y^2}}{64} = 1 \)
Thus, after comparing the above equation \(\frac{{x^2}}{100} + \frac{{y^2}}{64} = 1 \) by \(\frac{{x^2}}{{a^2}} + \frac{{y^2}}{{b^2}} = 1 \),
The values obtained are, a = 10 and b = 8.
Ques: Determine the equation of the ellipse that has a major axis along the x-axis, passing via the points (-3, 1) and (2, -2). (3 marks)
Ans: Because the points (-3, 1) and (2, -2) have been seen to lie on the ellipse,
Thus,
\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \frac{9^2}{a^2} + \frac{1^2}{b^2} = 1\) and, \(\frac{4^2}{a^2} + \frac{4^2}{b^2} = 1\)
Hence, it can be said that we have to equate both the equations together, hence:
\(a^2 = \frac{{32}}{3}\) and \(b^2 = \frac{{32}}{5} \)
Thus, the equation of the ellipse becomes:
\(\frac{{x^2}}{{\frac{{32}}{3}}} + \frac{{y^2}}{{\frac{{32}}{5}}} = 1 \)
Hence, 3x2 + 5y2 = 32
Ques: Determine the area of an ellipse which has major and minor axes are 14 in and 8 in respectively. (3 marks)
Ans: As per the given information, we have 2a = 14 in
Thus, we can say,
- a = 14/2 = 7
- 2b = 8 in ⇒ b = 8/2 = 4
Therefore, by applying the ellipse formula to obtain area, we get:
Area of ellipse = π(a)(b)
= π(7)(4)
= 28π
= 28(22/7)
= 88 in2
Ques: The semi-major and semi-minor axis’ length of an ellipse is given as 5 in and 3 in respectively. Thus, determine its eccentricity and the length of the latus rectum. (5 marks)
Ans: As per the Given: a = 5 in, and b = 3 in
Now, after applying the ellipse formula for eccentricity, we get:
\(e = \sqrt{1- \dfrac{ b^ 2}{ a^ 2} } \)
Thus, we can also say that:
√( 1 - 32 / 52 )
= √(1 - 9/25 )
= √((25 - 9)/25)
= √(16/25)
= 4/5
= 0.8
Thus, after applying the ellipse formula for latus rectum, we get:
L = 2b2/a
= 2(32)/5
= 2(9)/5
= 18/5
= 3.6 cm
The answers are: 0.8 and 3.6 cm.
Also Check:





Comments