Quotient rules fall under the subdomains of differentiation in calculus. It is one of the prominent topics of differentiation. Differentiation means breaking a function down into smaller functions. It is evident in problems related to differentiation where a function gets divided by the other quotient rule.
Read More: Negative of a Vector
The quotient rule in calculus is defined as the procedure to find the derivative of two functions that happen to be in a ratio and are differentiable too. The quotient rule can be applied to calculate the derivative of a function in such a pattern: f(x)/g(x), where both the f(x) and g(x) are differentiable and g(x)≠0. It follows both the understanding of limits of derivatives in differentiation and the product rule.
Read More: Formula Of Perimeter Shapes
The quotient rule is different from the product rule as in the quotient rule the function is of the form f(x)/g(x) while in the product rule it is of the form f(x)*g(x).
It is possible to calculate the high order derivatives by applying the concepts of the quotient rule. It may appear as difficult but once understood well along with the steps, and if followed all the steps in a defined manner, then it saves time and is one of the effective manners.
Discover about the Chapter video:
Continuity and Differentiability Detailed Video Explanation:
Read More: Fundamental Theorem of Calculus
The Formula of Quotient Rule
The quotient rule formula is given by:
f'(x) = [u(x)/v(x)]' = [v(x) × u'(x) - u(x) × v'(x)]/[v(x)]2
where,
- f(x) = The derivative to be calculated as a function in the form u(x)/v(x).
- u(x) = Numerator of the function f(x) which is differentiable.
- u'(x) = Derivative of function u(x).
- v(x) = Denominator of the function f(x) which is differentiable.
- v'(x) = Derivative of the function v(x).
Read More:
Derivation of Quotient Rule
The quotient rule can be derived using three different methods:
- Derivative and limit properties
- Implicit differentiation
- Chain rule?
Read More:
Proof using derivative and limit properties
The quotient rule can be derived using the derivative and limit properties.
Let us assume the function f(x) = u(x)/v(x)
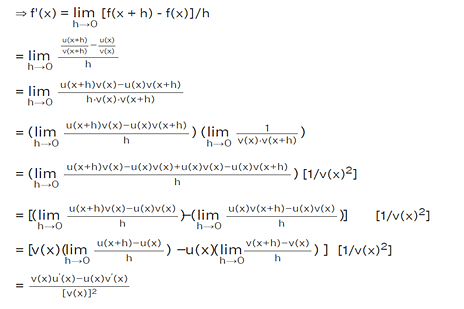
Proof Using Implicit Differentiation
Let us assume a differentiable function f(x)=u(x)/v(x), such that u(x) = f(x)⋅v(x)
Applying the product rule, u'(x) = f'(x)⋅v(x) + f(x)v'(x).
Calculating f(x), we have:
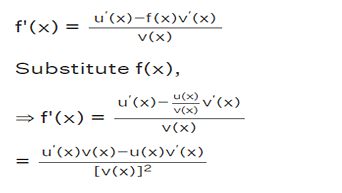
Proof Using the Chain Rule
Let us assume a differentiable function f(x) where f(x)=u(x)/v(x)

Steps to calculate the derivates using the quotient rule
Some of the steps required to obtain the derivative of any function using quotient rule are mentioned below:
- The functions should be in the division.
- Differentiating the function concerning anything applicable according to the question.
- If the function at LHS is y which is the same as the other function known as x then the derivative will be dy/dx.
- The RHS derivative will be equal to the upper function times the derivative of the lower function subtracted by the lower function times the derivative of the upper function divided by the square of the lower function.
- The equation obtained after simplification is the final answer.
Also Read:
Application of Quotient Rule in Differentiation
To calculate the derivative of any function of the pattern f(x)=u(x)/v(x), the condition should be that both of these u(x) and v(x) should be differentiable. If they are differentiable then one needs to follow the steps mentioned below to obtain the derivation of f(x)=u(x)/v(x) being a differentiable function according to the quotient rule.
The steps are:
Step 1: Write the values of u(x) and v(x).
Step 2: Obtain the values of u'(x) and v'(x) and then with respect to the quotient rule formula, one needs to solve the equation. The quotient rule formula is given as:
f'(x) = [u(x)/v(x)]' = [u'(x) × v(x) - u(x) × v'(x)]/[v(x)]2
Read More:
Examples
Let us assume a function f(x) such that
f(x) = g(x) / t(x)
the derivate of f(x) is given by:
f(x) = g(x) / t(x)
which suggests that the derivative obtained using the quotient rule is a combination of the initial function and its derivates.
Examples of these functions include six/ex, 3x/x4, e3x/2x, etc.
Read More:
Points to Remember
Following are some important points:
- Quotient Rule can be termed as the method to obtain the derivative of any two functions which happens to be both in ratio and differentiable.
- The quotient rule is different from the product rule as in the quotient rule the function is of the form f(x)/g(x) while in the product rule it is of the form f(x)*g(x).
- The quotient rule formula is given by: f'(x) = [u(x)/v(x)]' = [v(x) × u'(x) - u(x) × v'(x)]/[v(x)]2
- The quotient rule can be derived using three different methods namely derivative and limit properties, implicit differentiation, and the chain rule.
- If the functions u(x) and v(x) are differentiable and to calculate the derivate of a function, f(x)=u(x)/v(x), one needs to first write and values of u(x) and v(x) and then apply the formula of the quotient rule.
Read More:
Sample Questions
Ques: What is the formula of Quotient Rule?
Ans: The Formula of Quotient Rule is as follows:\(\frac{dy}{dx} = \frac{v \frac{du}{dx}-u \frac{dv}{dx}}{v^2} \)
Ques: For the function f(x)= x2/(x+1), calculate f'(x) by applying the quotient rule.
Ans: Given, f(x) = x2/ (x + 1)
u(x) = x2
v(x) = (x + 1)
⇒u'(x) = 2x
⇒v'(x) = 1
⇒f'(x) = [v(x)u'(x) - u(x)v'(x)]/[v(x)]2
⇒f'(x) = [(x+1) *2x - x2*1]/ (x + 1)2
⇒f'(x) = (2x2 + 2x - x2)/ (x + 1)2
⇒f'(x) = (x2 + 2x)/ (x + 1)2
Therefore, the derivative of the function f(x) = x2/(x+1) is (x2 + 2x)/ (x + 1)2.
Ques: Write a simple definition for Quotient Rule?
Ans: A Rule which is used to find out the derivative f any function which can be written as the quotient of two functions is known as Quotient Rule.
Also Read:
Ques: Calculate the derivative of the function \(f (x) = \frac{x^3}{1 - x^4}\) using quotient rule.
Ans: Calculation is as follows:

Ques: Calculate the derivative of the function using quotient rule where.
\(f (x) = \frac{x^2 + x - 2}{x^3 + 6}\)
Ans: Calculation is as follows:






Comments