
Content Curator
Factorial of a number is used extensively in permutations, combinations, and probability computation. It is signified by an exclamation mark (!). The product of a whole number 'n' with every whole number until 1 is called the factorial. The factorial of 4 is, for example, 4x3x2x1, which equals 24. So, the value of 4 is 24!
Fabian Stedman, a British author, defined factorial as the equivalent of change ringing in the year 1677. The musicians would ring various tuned bells as part of the musical performance known as change ringing. And it was in the year 1808 when Christian Kramp, a French mathematician, devised the symbol for factorial: n!
Factorial Definition
Factorial formula is defined as the sum of a number's lowest value until it reaches 1. As a consequence of multiplying the descending series of integers, this is the outcome. It's important to keep in mind that the factorial of 0 is 1. In permutations and combinations for probability computation, the Factorial Formula has several direct and indirect uses.Factorial functions include double factorial, multifactorial, and other variations. The Gamma function, which is based on factorial, is also an essential idea.
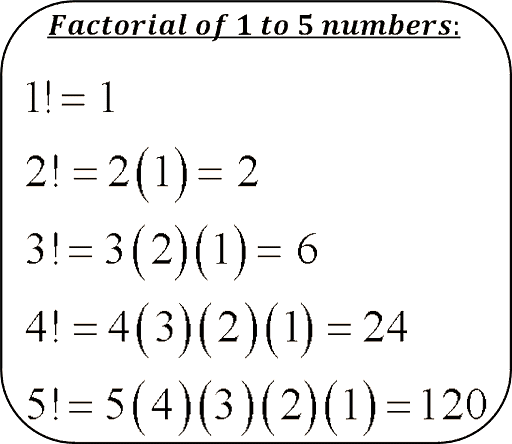
Factorial Formula
The following formula can be used to find the factorial of a given number n:
p!=p×(p−1)×(p−2)…×2×1
In addition, the above calculation can be performed as follows:
The factorial of a number n can be expressed as,
p!=p×(p−1)!
Alternatively, p!=px(p-1)(p-2)!
Because the factorial calculation is recursive, this is feasible.

Let's look at some examples to help us comprehend
45!43! = 43!×44×4543!=44×45
= 1980
Factorial Value Applications
The following are some examples of factorial applications in mathematics
Recursion
We can utilize factorial in the recursive definition of a number. A phrase containing only the number can be used to express a number.
p!=p
×(p–1)×(p–2)×(p–3)..(p−(p–2))
×(p–(p–1))
Permutations
When an order is critical, arranging given r items out of a total of n items.
Pnr=n!/(n−r)!
Combinations
When an order is not important, arranging given r items out of a total of n items.
Cnr=n!/(n−r)!r!
Distributions of Probability
There are other probability distributions, such as the binomial distribution, that use factorials. Permutations and combinations are frequently used to calculate the probability of an event.
Number Theory
Factorials are commonly employed in number theory and for approximations.
Things to Remember
- Factorials can be defined as a product of integers (n) upto 1. Factorial Formula for n factorial is n! = nx(n-1)!.
- The study of factorials is fundamental to many areas of mathematics, including number theory, algebra, geometry, probability, statistics, graph theory, and discrete mathematics, among others.
- Factorial of a number is a mathematical function where that number is multiplied by each natural number below it.
Sample Questions
Ques. What is the significance of factorial analysis? (2 marks)
Ans. It comes in handy when we're trying to count how many various ways we can combine things or how many possible orders there are for things. How many different ways can we arrange n items, for example? For the first thing, we have n options.
Ques. What are Factorials and what are they good for? (3 marks)
Ans. Factorial is the mathematical definition of multiplying any natural number by all the natural numbers that are smaller than it, giving us n! = n * (n - 1) * (n - 2) * (n - 3).... Finally, factorial is used to ask how many different ways you may arrange or organise a specific amount of items.
Ques. What exactly is a factorial? (2 marks)
Ans. The product of all positive integers less than or equal to a particular positive integer, indicated by that integer and an exclamation point in mathematics. As a result, factorial seven is expressed as 7!, which means 1x2x3x4x5x6x7. Factorial zero is defined as equal to 1.
Ques. What is the formula for calculating 100 factorials? (3 marks)
Ans. 120 = 5 * 4 * 3 * 2 * 1. It is simple to calculate using any programming language. The Factorial of 100, on the other hand, contains 158 digits. Even if we use "long long int," we won't be able to store this many numbers.
Ques. What does the term "3 factorial" mean? (2 marks)
Ans. 3! represents the factorial of three. The factorial of 3 means that we must multiply all whole numbers from 3 to1. The factorial of three is calculated in the following way: 3 (3!) factorial = 3 x 2 x 1. Factorial of 3 equals 6.
Ques. What are some of the uses of Factorials? (3 marks)
Ans. The factorial function can also be used to tally how many different ways you can choose from a set of options. Consider the following scenario: you're going on a trip and need to decide which T-shirts to bring. Assume you have n T-shirts but only have room to pack k of them.
Ques. What are the consequences of conducting a factorial study? (2 marks)
Ans. It has the ability to examine each component individually and discover its major effect. It can also determine possible interactions between components, which is something that other experimental designs couldn't achieve.
Ques. When do you think you'd employ Factorials in the real world? (2 marks)
Ans. Understand that the number of ways you can arrange the given objects is given by factorial of n items. For example, if you have two coins, you can arrange them in two different ways; if you have three coins, you can arrange them in six different ways.
Ques. What are the drawbacks of using a factorial design? (2 marks)
Ans. Factorial Design's Benefits and Drawbacks
The biggest downside is that experimenting with more than two elements or levels is difficult. A factorial design must be meticulously prepared, as a mistake in one of the levels, or in the overall operationalization, can imperil a significant amount of labor.
Ques. What are the three different types of factorial layouts? (3 marks)
Ans. Between subject factorial designs (all independent variables are modified between subjects), within-subject factorial designs (all independent variables are modified within-subjects), and mixed factorial designs (some independent variables are modified within and some between subjects) are the three types of factorial designs available.
Ques. What are the benefits of using a factorial design Quizlet? (2 marks)
Ans. A factorial design has the advantage of being able to quantify the interacting effects of two or more independent variables. Interaction effects, on the other hand, are the effects of two or more independent factors on the dependent variable when they are combined.
Ques. What method do you use to calculate permutations? (2 marks)
Ans. Take the number of options for each event and multiply it by itself X times, where X equals the number of events in the sequence, to get the number of permutations. With four-digit PINs, for example, each digit can vary from 0 to 9, giving us a total of ten options for each digit.
Ques. A 2x2x2 factorial design has how many major effects? (2 marks)
Ans. There are two primary consequences
Take, for example, 2x2 designs. The possibility of two major impacts and one interaction will always exist. For each primary effect and interaction, you will always be able to compare the means.





Comments