
Collegedunia Team Content Curator
Content Curator
Bisection method is a way to find solutions of a given equation with an unknown in Mathematics. It is one of the simplest methods to find the solution of a transcendental equation. The method is based on intermediate value and is easy to implement. Bisection method is known by many different names. Some of them are - the interval halving method, the binary search method, the dichotomy method, and Bolzano’s Method. The method treats the interval distance between the initial values as the line segment.
Read More: Face Value and Place Value
| Table of Contents |
Key terms: transcendental equation, dichotomy method, Bolzano theorem, Binary Chopping, interval halving, bracketing, numerical, polynomial
What is Bisection Method?
[Click Here for Sample Questions]
To find the roots of a polynomial equation, we use Bisection Method. Bisection method is the simplest among all the numerical methods to solve the transcendental equation. The intermediate theorem of continuous functions is the principle used behind this method. It separates the interval and further subdivides the interval within which the root of the equation must lie.
Bisection Method works by narrowing the gap between negative and the positive interval until it closes on the actual solution. Bisection method is quite simple but a relatively slow method. Bisection method is known by many different names. They are - interval halving method, root-finding method, binary search method or dichotomy method.
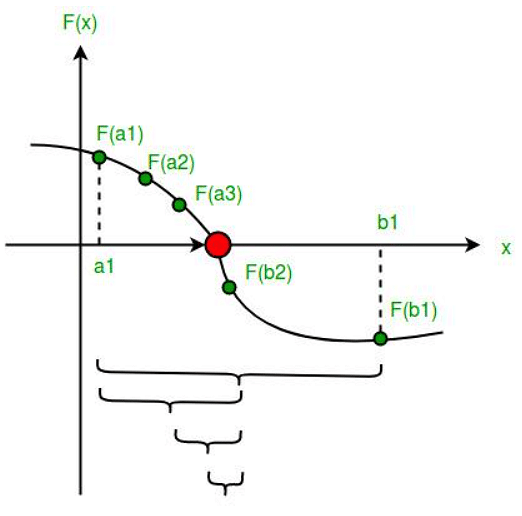
Bisection Method
Example- Bisection method is like the bracketing method. It begins with two initial guesses.Let the two initial guesses be x0 and x1 such that x0 and x1 brackets the root i.e. f(x0)f(x1)<0.
Now we know that Bisection Method is based on real and continuous functions. So, if f(x) is a real and continuous function, and for two initial guesses x0 and x1 brackets the root such that: f(x0)f(x1) <0 then there exists at least one root between x0 and x1.Since the root is obtained by halving the assumed guesses, then the new root obtained is - x2 = (x0 + x1)/2.
Thus we get the following three cases -
- If f(x2)=0 , then the root is x2
- If f(x0) f(x2)< 0, then the root lies between x2 and x0
- If f(x0) f(x2)> 0, then the root lies between x1 and x2
Bisection Method Algorithm
[Click Here for Sample Questions]
Given below are the steps that can be followed to get a solution for continuous function -
- Define the function f(x)
- Begin by choosing the two initial guesses. Let the two guesses be x0 and x1 such that f(x0)f(x1) < 0
- Choose pre-specified tolerable error
- Calculate the root obtained as x2 = (x0 + x1)/2
- Calculate f(x0)f(x2);
- if f(x0)f(x2) < 0 then x0 = x0 and x1 = x2
- if f(x0)f(x2) > 0 then x0 = x2 and x1 = x1
- if f(x0)f(x2) = 0 then follow the next step
- if |f(x2)| > e then go to step 5 else go to the next step
Bisection Method Procedure
[Click Here for Sample Questions]
Following steps can be followed to solve a transcendental equation using Bisection Method -
- Find out two distinct points say x and y in a manner that x is smaller than y and the value of their functions is less than 0. (f(a)* f(b) < 0, Bolzano Theorem)
- Next, find the middle point of the line segment or interval (x, y), say ‘z.’
- z will be the root of the function if and only if f(z) = 0; if not the root, follow the next step.
- Now we need to further divide the interval. If f(z) x f(x) <0, there exists a root or solution between z and x, else if f(z) x f (y) < 0, the root will exist between y and z.
- Keep following these steps until you get f(z) = 0.
Read Also: algebra introduction different branches of algebra equations
Bolzano Theorem
[Click Here for Sample Questions]
Bisection Method which is also known as the interval halving method is based on the Bolzano Theorem. According to the Bolzano theorem ,if on an interval a,b and f(a)·f(b) < 0, a function f(x) is found to be continuous, then there exists a value c such that c ∈ (a, b) or which f(c) = 0.
Advantages of Bisection Method
[Click Here for Sample Questions]
- Convergence is guaranteed by Bisection Method
- By increasing the number of iterations, the root obtained can be more accurate
- Calculations are sorted and are not much complex
- It is a very simple method to solve a transcendental equation
Disadvantages of Bisection Method
[Click Here for Sample Questions]
- Though Bisection Method guarantees convergence, it is a relatively slow method
- The rate of convergence is linear
- The method cannot be applied over an interval where the function returns values of the same sign.
Read Also: permutations and combinations formula examples questions
Things To Remember
- Bisection Method also known as the bracketing method offers guaranteed convergence. But, though the convergence is guaranteed, this method is relatively slow.
- Roots of some of the equations cannot be found because there are no bracketing values, like f(x) = x².
- Bisection Method guarantees error bound which reduces with each repetition . After every cycle, error bound is reduced by 12%.
- The rate of convergence in Bisection Method is linear
- The method cannot be used to determine complex roots. Also, if the guess intervals have discontinuities , then the method cannot be used.
Read Also: Quadratic equations formula definition methods and examples
Sample Questions
Ques.Using Bisection Method , find the root of an equation f(x)=x3-x-1. (3 Marks)
Ans: Here x3-x-1=0
Let f(x)=x 3-x-1
Here
| x | 0 | 1 | 2 |
| f(x) | -1 | -1 | 5 |
1st iteration :
Here f(1)=-1<0 and f(2)=5>0
∴ Now, Root lies between 1 and 2
x 0=1+2/2=1.5
f(x 0)=f(1.5)=0.875>0
2nd iteration :
Here f(1)=-1<0 and f(1.5)=0.875>0
∴ Now, Root lies between 1 and 1.5
x 1=1+1.5/2=1.25
f(x 1)=f(1.25)=-0.29688<0
3rd iteration :
Here f(1.25)=-0.29688<0 and f(1.5)=0.875>0
∴ Now, Root lies between 1.25 and 1.5
x2 =1.25+1.5/2=1.375
4th iteration :
Here f(1.25)=-0.29688<0 and f(1.375)=0.22461>0
∴ Now, Root lies between 1.25 and 1.375
X 3=1.25+1.3752=1.3125
f(x 3)=f(1.3125)=-0.05151<0
5th iteration :
Here f(1.3125)=-0.05151<0 and f(1.375)=0.22461>0
∴ Now, Root lies between 1.3125 and 1.375
X 4=1.3125+1.375/2=1.34375
f(x 4)=f(1.34375)=0.08261>0
6th iteration :
Here f(1.3125)=-0.05151<0 and f(1.34375)=0.08261>0
∴ Now, Root lies between 1.3125 and 1.34375
X 5=1.3125+1.34375/2=1.32812
f(x 5)=f(1.32812)=0.01458>0
7th iteration :
Here f(1.3125)=-0.05151<0 and f(1.32812)=0.01458>0
∴ Now, Root lies between 1.3125 and 1.32812
X 6=1.3125+1.32812/2=1.32031
f(x 6)=f(1.32031)=-0.01871<0
8th iteration :
Here f(1.32031)=-0.01871<0 and f(1.32812)=0.01458>0
∴ Now, Root lies between 1.32031 and 1.32812
X 7=1.32031+1.32812/2=1.32422
f(x 7)=f(1.32422)=-0.00213<0
9th iteration :
Here f(1.32422)=-0.00213<0 and f(1.32812)=0.01458>0
∴ Now, Root lies between 1.32422 and 1.32812
X 8=1.32422+1.32812/2=1.32617
f(x 8)=f(1.32617)=0.00621>0
10th iteration :
Here f(1.32422)=-0.00213<0 and f(1.32617)=0.00621>0
∴ Now, Root lies between 1.32422 and 1.32617
X 9=1.32422+1.32617/2=1.3252
f(x 9)=f(1.3252)=0.00204>0
11th iteration :
Here f(1.32422)=-0.00213<0 and f(1.3252)=0.00204>0
∴ Now, Root lies between 1.32422 and 1.3252
X 10=1.32422+1.3252/2=1.32471
f(x 10)=f(1.32471)=-0.00005<0
Approximate root of the equation x3-x-1=0 using Bisection method is 1.32471
| n | a | f(a) | b | f(b) | c=a+b2 | f(c) | Update |
|---|---|---|---|---|---|---|---|
| 1 | 1 | -1 | 2 | 5 | 1.5 | 0.875 | b=c |
| 2 | 1 | -1 | 1.5 | 0.875 | 1.25 | -0.29688 | a=c |
| 3 | 1.25 | -0.29688 | 1.5 | 0.875 | 1.375 | 0.22461 | b=c |
| 4 | 1.25 | -0.29688 | 1.375 | 0.22461 | 1.3125 | -0.05151 | a=c |
| 5 | 1.3125 | -0.05151 | 1.375 | 0.22461 | 1.34375 | 0.08261 | b=c |
| 6 | 1.3125 | -0.05151 | 1.34375 | 0.08261 | 1.32812 | 0.01458 | b=c |
| 7 | 1.3125 | -0.05151 | 1.32812 | 0.01458 | 1.32031 | -0.01871 | a=c |
| 8 | 1.32031 | -0.01871 | 1.32812 | 0.01458 | 1.32422 | -0.00213 | a=c |
| 9 | 1.32422 | -0.00213 | 1.32812 | 0.01458 | 1.32617 | 0.00621 | b=c |
| 10 | 1.32422 | -0.00213 | 1.32617 | 0.00621 | 1.3252 | 0.00204 | b=c |
| 11 | 1.32422 | -0.00213 | 1.3252 | 0.00204 | 1.32471 | -0.00005 | a=c |
Ques. Using Bisection method find the root of cos(x) – x * ex = 0 with a = 0 and b = 1 (3 Marks)
Ans. Iteration table is given as follows
| Number | a | b | c | f(a)*f(c) |
|---|---|---|---|---|
| 1 | 0 | 1 | 0.5 | 0.053 |
| 2 | 0.5 | 1 | 0.75 | -0.046 |
| 3 | 0.5 | 0.75 | 0.625 | -0.357 |
| 4 | 0.5 | 0.625 | 0.562 | -7.52*10-3 |
| 5 | 0.5 | 0.562 | 0.531 | -2.168*10-3 |
| 6 | 0.5 | 0.531 | 0.516 | 3.648*10-4 |
| 7 | 0.516 | 0.531 | 0.524 | -9.371*10-5 |
| 8 | 0.516 | 0.524 | 0.520 | -3.649*10-5 |
| 9 | 0.516 | 0.520 | 0.518 | -3.941*10-6 |
| 10 | 0.516 | 0.516 | 0.517 | 1.229*10-5 |
The difference between final values is less than 0.01 hence we stop the iterations. So one of the roots of cos(x) – x * exp(x) = 0 is approximately 0.517.
Ques.A function is defined as f(x) = x2 – 3. Between the interval [1,2] find the root of the function by Bisection Method (3 Marks)
Ans-
| a | b | f(a) | f(b) | c = (a+b)/2 | f(c) | Substitution | new b-a |
|---|---|---|---|---|---|---|---|
| 1 | 2 | -2 | 1 | 1.5 | -0.75 | a=c | 0.5 |
| 1.5 | 2 | -0.75 | 1 | 1.75 | 0.062 | b=c | 0.25 |
| 1.5 | 1.75 | -0.75 | 0.0625 | 1.625 | -0.359 | a=c | 0.125 |
| 1.625 | 1.75 | -0.75 | 0.0625 | 1.6875 | -0.1523 | a=c | 0.0625 |
| 1.625 | 1.75 | -0.3594 | 0.0625 | 1.6875 | -0.1523 | a=c | 0.0625 |
| 1.6875 | 1.75 | -0.1523 | 0.0625 | 1.7188 | -0.0457 | a=c | 0.0313 |
| 1.7188 | 1.75 | -0.0457 | 0.0625 | 1.7344 | 0.0081 | b=c | 0.0156 |
| 1.7266 | 1.7344 | -0.0457 | 0.0081 | 1.7266 | -0.0189 | a=c | 0.0078 |
Thus, with the seventh iteration, we can see that final interval, [1.7266, 1.7344], has a width less than 0.01 and |f(1.7344)| < 0.01. Hence we chose b = 1.7344 to be our approximation of the root
Ques.What does f(a)f(b) 0 stand for? (3 Marks)
Ques.What are the applications of Bisection Method? (5 Marks)
Ans. Some of the possible applications of Bisection Method are -
- To determine the appropriate size of the population
- To locate and compute periodic orbits in a molecular system and some more
- To detect short segments in video content for a video library
- Scientific Recommending
- construct the continuation/bifurcation diagram of the bend mode family.
Ques.When can a function be said to be continuous? (5 Marks)
Ans. When minor changes in the parameter cause small changes in the result, the function is said to be continuous. Minor changes in x, for example, will result in small changes in f(x). If the change in x is made in small increments, the change in f(x) will be made in little steps as well, rather than large "jumps." This demonstrates that the argument and the result are directly proportional, meaning that if one rises, the other rises with it. A function becomes continuous as a result of this.
Ques.What is the minimum number of iterations required to achieve accuracy upto two decimal points if one real root of the polynomial P(x) = X3 - X - 1 lies in the interval [1,2] and bisection method is used to find its value? (3 Marks)
Ans. To achieve accuracy up to two decimal places means that the arrow between the real root and numerically calculated root should be less than 0.01
€<0.01
f(x) = x³-x-1, 1≤ × ≤2
Accuracy = 0.01
Accuracy of bisection method is given by,
€≥(b-a/2n)
→ 0.01 ≥ (2-1/2n)
→0.01≥1/2n
→2n≥100
Therefore the minimum number of n to satisfy the above condition is n = 7
Ques. Use Bisection Method to find out the root of x – sinx – 0.5 = 0 between 1 and 2. (5 Marks)
Ans.Iteration table is given as follows:
| No. | a | b | c | f(a)*f(b) |
|---|---|---|---|---|
| 1 | 1 | 2 | 1.5 | -8.554*10-4(-) |
| 2 | 1 | 1.5 | 1.25 | 0.068(+) |
| 3 | 1.25 | 1.5 | 1.375 | 0.021(+) |
| 4 | 1.375 | 1.5 | 1.437 | 5.679*10-3(+) |
| 5 | 1.437 | 1.5 | 1.469 | 1.42*10-3(+) |
| 6 | 1.469 | 1.5 | 1.485 | 3.042*10-4(+) |
| 7 | 1.485 | 1.5 | 1.493 | 5.023*10-5(+) |
| 8 | 1.493 | 1.5 | 1.497 | 2.947*10-6(+) |
Since the difference between b and c is less than 0.01 we stop the iterations. So one of the roots of x-sinx – 0.5 = 0 is approximately 1.497.
Ques.Find a root of f (x) = 3x + sin(x) – ex = 0. Use 6 iterations to find the approximate value of x. (3 Marks)
Ans. The iteration table is given as follows:
| No. | a | b | c | f(a)*f(b) |
|---|---|---|---|---|
| 1 | 0 | 0.5 | 0.25 | 0.287(+ve) |
| 2 | 0.25 | 0.5 | 0.393 | -0.015(-ve) |
| 3 | 0.65 | 0.393 | 0.34 | 9.69(+ve) |
| 4 | 0.34 | 0.393 | 0.367 | -7.81(-ve) |
| 5 | 0.34 | 0.367 | 0.354 | 8.9(+ve) |
| 6 | 0.354 | 0.367 | 0.3605 | -3.1(-ve) |
We have to find the value of x approximated to 6 iterations. So one of the roots of 3x + sin(x) – ex = 0 is approximately 0.3605
Ques.Find the approximated value of x till 4 iterations for e-x = 3 log(x) using Bisection Method. (3 Marks)
Ans. The Iteration table is given as follows.
| No. | a | b | c | f(a)*f(b) |
|---|---|---|---|---|
| 1 | 0.5 | 1.5 | 1 | 0.555(+ve) |
| 2 | 1 | 1.5 | 1.25 | -1.555*10-3(-ve) |
| 3 | 1 | 1.25 | 1.125 | 0.063(+ve) |
| 4 | 1.125 | 1.25 | 1.187 | 0.014(+ve) |
Hence we stop the iterations after 4. Therefore the approximated value of x is 1.187.
Ques.What is the other name for Bisection Method? (2 Marks)
Ans. Bisection method is also known as the Binary Chopping Method as it involves the division of the interval into half.
Ques. A function f(x) is given as e-x * (x2 +5x+2) + 1 = 0. Let a = 0 and b = -1. Find the root between a and b using Bisection Method. (3 Marks)
Ans. Iteration table is given as follows:
| No. | a | B | c | f(a)*f(c) |
|---|---|---|---|---|
| 1 | 0 | -1 | -0.5 | 1.763(+ve) |
| 2 | -0.5 | -1 | -0.75 | -0.89(-ve) |
| 3 | -0.5 | -0.75 | -0.625 | -0.219(-ve) |
| 4 | -0.5 | -0.625 | -0.562 | 0.076(+ve) |
| 5 | -0.562 | -0.625 | -0.593 | -0.015(-ve) |
| 6 | -0.562 | -0.593 | -0.577 | 1.733*10-3(+ve) |
The difference between the final iterating values is less than 0.01. So one of the roots of e-x * (x2 -5x+2) + 1 = 0 is approximately -0.577.
Read Also:







Comments