
Content Curator
Construction is a part of Geometry that helps us in understanding how we can draw shapes, angles, or lines accurately. There are various construction methods to precisely construct many geometric figures. These constructions are done by using a compass, ruler, and pencil. At a complex level, geometric constructions are done using high-level machinery and application systems.
| Table of Content |
Key Takeaways: Triangle, Angle Bisector, Perpendicular Bisector, line segment.
Also Read: Trigonometry Identities
Construction of Angle Bisector
[Click Here for Sample Questions]
Angle bisector is that line segment which bisects or divides an angle into two equal parts.
Steps of Construction:
- Take any radius of your choice and draw an arc taking B as the centre. Intersect the rays BA and BC with the arc, say at E and D, respectively.
- Now, take a radius of more than 1/2 DE, and take D and E as centres. Draw arcs to intersect each other, say at F.
- Join the points B and F, to form a ray BF, which is the required bisector of the ∠ABC.
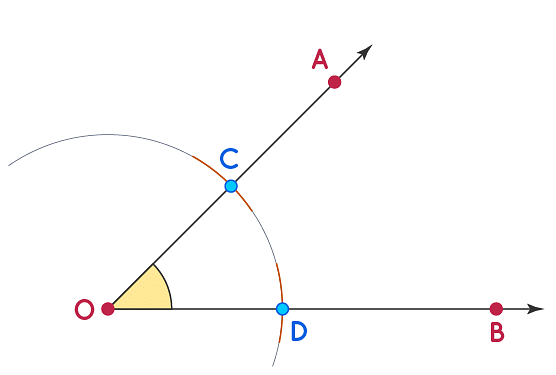
Angle Bisector Construction
Also Read:
| Related Articles | ||
|---|---|---|
| Circles | Triangles | Similarities of Triangle |
| Pythagoras Theorem | Trigonometric Identities | Construction Formula |
Construction of a Perpendicular Bisector
[Click Here for Sample Questions]
Perpendicular bisector is a line segment which divides a line into two equal parts.
Steps of Construction
- Draw a line AB of a certain length.
- Taking A and B as centers and a radius more than 1/2 AB, draw arcs on both the sides of the line segment AB, in such a way that they intersect each other at points P and Q.
- Let these points join to form the line PQ and intersect AB at point M.
- The line obtained, that is PMQ, is the required perpendicular bisector of AB.

Perpendicular Bisector Construction
Constructing an Angle of the Measure 60°
[Click Here for Sample Questions]
Angles between 0° and 90° are called an acute angle. To construct an acute angle of the measure 60°, the following steps are to be followed.
Steps of Construction
- Take any radius of your choice, and draw an arc taking A as the center of a circle that intersects the line AB, at a point D.
- Take the same radius as before, and draw an arc taking D as the center, in such a way that it intersects the previously drawn arc, say at a point E.
- Join the points A and E to form a ray AEC.
- So, ∠CAB is the required angle of 60°.

Construction of 60° angle
Also Read: Surface Areas and Volumes
Construction of Triangle
[Click Here for Sample Questions]
Triangle is a three-sided polygon having three vertices. The sum of all interior angles of any triangle is 180°. The following steps are to be followed to construct a right angled triangle.
Given: base, base angle, and the sum of the other two sides
Steps of Construction:
(i) Draw the base BC and at point B, makes an angle, say ∠XBC equal to the given angle.
(ii) Cut a line segment BD equal to AB + AC from the ray BX.
(iii) Join DC and make an angle ∠DCY equal to ∠BDC.
(iv) Let CY intersect BX at A.

Triangle ABC is the required triangle.
Given: Base, Base angle and the difference of other two sides
Case (I): Let AB > AC, i.e., AB-AC is given.
Steps of Construction
- Draw the base BC and at point, B makes an angle, say ∠XBC equal to the given angle.
- Cut the line segment BD equal to AB – AC from ray BX.
- Join DC and draw the perpendicular bisector, say PQ of DC.
- Let it intersect BX at a point A. Join AC.
Then, triangle ABC is the required triangle.
Case (II): Let AB < AC i.e., AC – AB be given.
Steps of Construction
- Draw the base BC and at point, B makes an angle, say ∠XBC equal to the given angle.
- Cutline segment BD equal to AC – AB from the line BX extended on the opposite side of line segment BC.
- Join DC and draw the perpendicular bisector, say PQ of DC.
- Let PQ intersect BX at A. Join AC.
Then, ABC is the required triangle.
Given: Perimeter and the two base angles
Steps of Construction
- Draw a line segment, say XY equal to BC + CA + AB.
- Make angles LXY equal to ∠B and MYX equal to ∠C.
- Bisect ∠LYX and ∠MYX. Let these bisectors intersect a point A.
- Draw perpendicular bisectors PQ of AX and RS of AY.
- Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC.
Things to Remember
- There are various construction methods to precisely construct many geometric figures.
- These constructions are done by using a compass, ruler, and pencil.
- Angle bisector is that line segment which bisects or divides an angle into two equal parts.
- Perpendicular bisector is a line segment which divides a line into two equal parts.
- Angles between 0° and 90° are called an acute angle.
Also Read:
Sample Questions
Ques: What do you mean by the term 'angle bisector'? (2 marks)
Ans: An angle bisector refers to a line or a line segment that divides an angle into two equal parts.
For example, in the given case, BF is the angle bisector of ABC as ABF = CBF.
Ques: Explain how the methods followed to construct an angle bisector are correct? (2 marks)
Ans: Join DF and EF.
In ΔBEF and ΔBDF,
BE = BD (Radii of the same arc made by B as a centre)
EF = DF (Arcs of radii centres E and D)
BF = BF (Common side)
Therefore, ΔBEF = ΔBDF (SSS rule)
And hence, ∠EBF = ∠DBF (CPCT)
Ques: What do you mean by the term 'perpendicular bisector'? (2 marks)
Ans: A perpendicular bisector refers to a line or a line segment that bisects a line segment into two equal parts, by intersecting at its midpoint at right angles.
In this case, PMQ is the required perpendicular bisector of AB, as AM = BM, and PQ is perpendicular to AB.
Ques: Explain how the methods followed to construct a perpendicular bisector are correct? (5 marks)
Ans: Join the points, A and B to both, P and Q to form the line segments AP, AQ, BP, and BQ.
In ΔPAQ and ΔPBQ,
AP = BP (Arcs of equal radii with centers at A and B respectively)
AQ = BQ (Arcs of equal radii with centers at A and B respectively)
PQ = PQ (Common side)
Therefore, ΔPAQ = ΔPBQ (SSS rule)
So, ∠APM = ∠BPM (CPCT)
Now, in ΔPMA and ΔPMB,
AP = BP (Arcs of equal radii with centres at A and B respectively)
PM = PM (Common side)
∠APM = ∠BPM (Proved above)
Therefore, ΔPMA = ΔPMB (SAS rule)
And hence, AM = BM and ∠PMA = ∠PMB (CPCT)
As ∠PMA + ∠PMB = 180° (Linear pair axiom)
We get, ∠PMA = ∠PMB = 90°
Therefore, the line segment PQ or PMQ is the perpendicular bisector of AB.
Ques: Explain how the method followed to construct an angle of the measure of 60 degrees is correct? (2 marks)
Ans: Join DE.
According to the construction, AB = AD = DE
Therefore, ΔEAD is an equilateral triangle, and so, all its angles are of the measure 60 degrees. So, ∠CAB is equal to 60°.
Ques: What is the Linear Pair Axiom? (2 marks)
Ans: The linear pair axiom states that if a ray stands on a line, then the adjacent angles form a linear pair of angles.
Similarly, its converse is also true, i.e. if two angles form a linear pair, then uncommon arms of both the angles form a straight line.
Ques. Lengths of two sides of an isosceles triangle are 5 cm and 8 cm, find the perimeter of the triangle. (2 marks)
Ans. Since the lengths of any two sides of an isosceles triangle are equal, then
Case I: The three sides of the triangle are 5 cm, 5 cm and 8 cm.
Perimeter of the triangle = 5 cm + 5 cm + 8 cm = 18 cm
Case II: The three sides of the triangle are 5 cm, 8 cm and 8 cm.
Perimeter of the triangle = 5 cm + 8 cm + 8 cm = 21 cm
Hence, the required perimeter is 18 cm or 21 cm.
Ques. In the given figure, AP = BQ, PR = QS. Show that ΔAPS = ΔBQR. (2 marks)
Ans. In ΔAPS and ΔBQR
AP = BQ (Given)
PR = QS (Given)
PR + RS = QS + RS (Adding RS to both sides)
PS = QR
∠APS = ∠BQR = 90° (Given)
ΔAPS = ΔBQR (by SAS rule)
Ques. In the following figure, show that ΔPSQ = ΔPSR. (2 marks)
Ans. In ΔPSQ and ΔPSR
PQ = PR = 6.5 cm (Given)
PS = PS (Common)
∠PSQ = ∠PSR = 90° (Given)
ΔPSQ = ΔPSR (By RHS rule)
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Check:






Comments